Геометрия

Геоме́трия (от др.-греч. γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Предложенный Декартом в 1637 году координатный метод лёг в основу аналитической и дифференциальной геометрии, а задачи, связанные с черчением, привели к созданию начертательной и проективной геометрии. При этом все построения оставались в рамках аксиоматического подхода Евклида. Коренные изменения связаны с работами Лобачевского в 1829 году, который отказался от аксиомы параллельности и создал новую неевклидову геометрию, определив таким образом путь дальнейшего развития науки и создания новых теорий.

Классификация геометрии, предложенная Клейном в «Эрлангенской программе» в 1872 году и содержащая в своей основе инвариантность геометрических объектов относительно различных групп преобразований, сохраняется до сих пор.

Предмет геометрии

Геометрия занимается взаимным расположением тел, которое выражается в прикосновении или прилегании друг к другу, расположением «между», «внутри» и так далее; величиной тел, то есть понятиями о равенстве тел, «больше» или «меньше»; а также преобразованиями тел. Геометрическое тело представляет собой абстракцию ещё со времён Евклида, который полагал, что «линия есть длина без ширины», «поверхность есть то, что имеет длину и ширину». Точка представляет собой абстракцию, связанную с неограниченным уменьшением всех размеров тела, или пределом бесконечного деления. Расположение, размеры и преобразования геометрических фигур определяются пространственными отношениями.

Исследуя реальные предметы, геометрия рассматривает только их форму и взаимное расположение, отвлекаясь от других свойств предметов, таких как плотность, вес, цвет. Это позволяет перейти от пространственных отношений между реальными объектами к любым отношениям и формам, возникающим при рассмотрении однородных объектов, и сходным с пространственными. В частности, геометрия позволяет рассматривать расстояния между функциями.

Классификация

Общепринятую в наши дни классификацию различных разделов геометрии предложил Феликс Клейн в своей «Эрлангенской программе» (1872). Согласно Клейну, каждый раздел изучает те свойства геометрических объектов, которые сохраняются (инвариантны) при действии некоторой группы преобразований, специфичной для каждого раздела. В соответствии с этой классификацией, в классической геометрии можно выделить следующие основные разделы.

• Евклидова геометрия, в которой предполагается, что размеры отрезков и углов при перемещении фигур на плоскости не меняются. Другими словами, это теория тех свойств фигур, которые сохраняются при их переносе, вращении и отражении.
  • Планиметрия — раздел евклидовой геометрии, исследующий фигуры на плоскости.
  • Стереометрия — раздел евклидовой геометрии, в котором изучаются фигуры в пространстве.
• Проективная геометрия, изучающую проективные свойства фигур, то есть свойства, сохраняющиеся при их проективных преобразованиях.
• Аффинная геометрия, изучающая свойства фигур, сохраняющиеся при аффинных преобразованиях.
• Начертательная геометрия — инженерная дисциплина, в основе которой лежит метод проекций. Этот метод использует две и более проекций (ортогональных или косоугольных), что позволяет представить трехмерный объект на плоскости.

Современная геометрия включает в себя следующие дополнительные разделы.

• Многомерная геометрия.
• Неевклидовы геометрии.
  • Сферическая геометрия.
  • Геометрия Лобачевского.
• Риманова геометрия.
• Геометрия многообразий.
• Топология — наука о непрерывных преобразованиях самого общего вида, то есть свойства объектов, которые остаются неизменными при непрерывных деформациях. В топологии не рассматриваются никакие метрические свойства объектов.

По используемым методам выделяют также такие инструментальные подразделы.

• Аналитическая геометрия — геометрия координатного метода. В ней геометрические объекты описываются алгебраическими уравнениями в декартовых (иногда аффинных) координатах и затем исследуются методами алгебры и анализа.
• Алгебраическая геометрия — изучает алгебраические многообразия (то есть множества, которые задаются полиномиальными уравнениями) с помощью методов современной общей алгебры.
• Дифференциальная геометрия — изучает линии и поверхности, задающиеся дифференцируемыми функциями, с помощью дифференциальных уравнений и методов топологии.

Аксиоматика

Аксиомы евклидовой геометрии, сформулированные в III—IV веке до н. э., составляли основу геометрии до второй половины XIX века, так как хорошо описывали физическое пространство и отождествлялись с ним. Пяти постулатов Евклида было недостаточно для полного описания геометрии и в 1899 году Гильберт предложил свою систему аксиом. Гильберт разделил аксиомы на несколько групп: аксиомы принадлежности, конгруэнтности, непрерывности (в том числе аксиома Архимеда), полноты и параллельности. Позднее Шур заменил аксиомы конгруэнтности аксиомами движения, а вместо аксиомы полноты стали использовать аксиому Кантора. Система аксиом евклидовой геометрии позволяет доказать все известные школьные теоремы.

Существуют и другие системы аксиом, в основе которых, помимо точки, прямой и плоскости, лежит не движение, а конгруэнтность, как у Гильберта, или расстояние, как у Кагана. Другая система аксиом связана с понятием вектора. Все они выводятся одна из другой, то есть аксиомы в одной системе можно доказать как теоремы в другой.

Для доказательства непротиворечивости и полноты аксиом евклидовой геометрии строят её арифметическая модель и показывают, что любая модель изоморфна арифметической, а значит они изоморфны между собой. Независимость аксиом евклидовой геометрии показать сложнее из-за большого количества аксиом. Аксиома параллельности не зависит от других, так как на противоположном утверждении строится геометрия Лобачевского. Аналогично была показана независимость аксиомы Архимеда (в качестве координат вместо тройки вещественных чисел используется тройка комплексных чисел), аксиомы Кантора (в качестве координат вместо тройки любых вещественных чисел используются вещественные числа, построенные определённым образом), а также одной из аксиом принадлежности, которая фактически определяет размерность пространства (вместо трёхмерного пространства можно построить четырёхмерное, и любое многомерное пространство с конечным числом измерений).

Постулаты Евклида

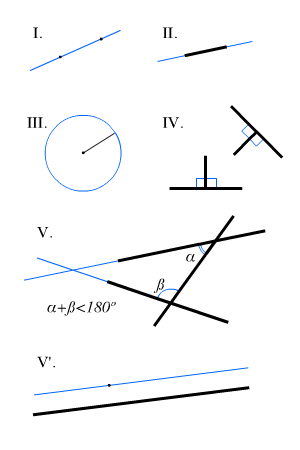Постулаты Евклида представляют собой правила построения с помощью идеального циркуля и идеальной линейки:

1. Всякие две точки можно соединить прямой линией;
2. Ограниченную прямую линию можно неограниченно продолжить;
3. Из всякого центра всяким радиусом можно описать окружность;
4. Все прямые углы равны между собой;
5. Если прямая падает на две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то при неограниченном продолжении этих двух прямых они пересекутся с той стороны, где углы меньше двух прямых.

Другая формулировка пятого постулата (аксиомы параллельности), гласит: Через точку вне прямой в их плоскости можно провести не более одной прямой, не пересекающей данную прямую.

Аксиомы евклидовой геометрии

В «Энциклопедии элементарной математики» предлагается следующая система аксиом:

• Аксиомы принадлежности:

1. Через каждые две различные точки проходит прямая и притом одна;
2. На каждой прямой имеется по крайней мере две точки;
3. Существуют три точки, не лежащие на одной прямой;
4. Через каждые три точки не лежащие на одной прямой проходит плоскость и притом только одна;
5. На каждой плоскости имеется по крайней мере одна точка;
6. Если две точки лежат на плоскости, то и проходящая через них прямая лежит на этой плоскости;
7. Если две плоскости имеют общую точку, они имеют по крайней мере ещё одну общую точку;
8. Существуют четыре точки, не лежащие на одной плоскости.
   • Аксиомы порядка:
9. Из любых трёх различных точек прямой одна и только одна лежит между двумя другими;
10. Для всяких двух точек прямой существует на этой прямой такая третья точка, что вторая точка лежит между первой и третьей;
11. Если прямая l, лежащая в плоскости ABC, не проходит ни через одну из точек A, B, C и содержит одну точку отрезка AB, то она имеет общую точку с хотя бы одним из отрезков AC, BC;
    • Аксиомы движения:
12. Всякое движение является взаимно однозначным отображением пространства на себя;
13. Пусть f — произвольное движение. Тогда, если точки A, B, C расположены на одной прямой, причём C лежит между A и B, то точки f(A), f(B), f(C) также расположены на одной прямой, причём f(C) лежит между f(A) и f(B);
14. Два движения, произведённые один за другим, равносильны некоторому одному движению;
15. Для всяких двух реперов, взятых в определённом порядке, существует одно и только одно движение, переводящее первый репер во второй;
    • Аксиомы непрерывности:
16. Аксиома Архимеда. Пусть A₀, A₁, B — три точки, лежащие на одной прямой, причём точка A₁ находится между A₀ и B. Пусть далее f — движение, переводящее точку A₀ в A₁ и луч A₀B в A₁B. Положим f(A₁)=A₂, f(A₂)=A₃, …. Тогда существует такое натуральное число n, что точка B находится на отрезке A_n-1A_n.
17. Аксиома Кантора. Пусть A₁, A₂, … и B₁, B₂, … — такие две последовательности точек, расположенных на одной прямой l, что для любого n точки A_n и B_n различны между собой и лежат на отрезке A_n-1B_n-1. Тогда на прямой l существует такая точка C, которая находится на отрезке A_nB_n при всех значениях n.
    • Аксиома параллельности:
18. Через точку A, не лежащую на прямой l, можно провести в их плоскости не более одной прямой, не пересекающей прямую l.

Если убрать из системы аксиомы 4-8, относящиеся к пространственной геометрии, то получится система аксиом евклидовой плоскости.

Геометрические преобразования

Преобразованием множества называют его взаимно-однозначное отображение на себя. В таком смысле этот термин используется в геометрии, хотя иногда его используют и как синоним отображения или отображения множества в себя.

Говоря о «геометрических преобразованиях», обычно имеют в виду некоторые конкретные типы преобразований, играющие фундаментальную роль в геометрии — движения, преобразования подобия, аффинные, проективные, круговые преобразования (в последних двух случаях плоскость или пространство дополняют бесконечно удаленными точками). Эту фундаментальную роль выявил Ф.Клейн в своей лекции в университете г. Эрланген (1872 г.), известной как Эрлангенская программа. Согласно концепции Клейна, геометрия изучает свойства фигур, сохраняющиеся при всех преобразованиях некоторой группы преобразований. Рассматривая группы преобразований указанных выше видов, получают разные геометрии — евклидову (для преобразований подобия), аффинную и т. д.

История

Традиционно считается, что родоначальниками геометрии как систематической науки являются древние греки, перенявшие у египтян ремесло землемерия и измерения объёмов тел и превратившие его в строгую научную дисциплину. При этом античные геометры от набора рецептов перешли к установлению общих закономерностей, составили первые систематические и доказательные труды по геометрии. Центральное место среди них занимают составленные около 300 до н. э. «Начала» Евклида. Этот труд более двух тысячелетий считался образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом. Первые же доказательства геометрических утверждений появились в работах Фалеса и использовали, по всей видимости, принцип наложения, когда фигуры, равенство которых необходимо доказать, накладывались друг на друга.

Геометрия греков, называемая сегодня евклидовой, или элементарной, занималась изучением простейших форм: прямых, плоскостей, отрезков, правильных многоугольников и многогранников, конических сечений, а также шаров, цилиндров, призм, пирамид и конусов. Вычислялись их площади и объёмы. Преобразования в основном ограничивались подобием. В Греции в работах Гиппарха и Менелая также появились тригонометрия и геометрия на сфере.

Средние века немного дали геометрии, и следующим великим событием в её истории стало открытие Декартом в XVII веке координатного метода (трактат «Геометрия», 1637). Точкам пространства сопоставляются наборы чисел, это позволяет изучать отношения между геометрическими формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями. Систематическое изложение аналитической геометрии было предложено Эйлером в 1748 году. В начале XVII века Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии и был впервые обобщён Понселе в 1822 году. Ещё раньше, в 1799 году Монж развил начертательную геометрию, связанную напрямую с задачами черчения. Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями. Дифференциальная геометрия была систематизирована Монжем в 1795 году, её развитием, в частности теорией кривых и теорией поверхностей, занимался Гаусс. На стыке геометрии, алгебры и анализа возникли векторное исчисление, тензорное исчисление, метод дифференциальных форм.

В 1826 году Лобачевский, отказавшись от аксиомы параллельности Евклида построил неевклидову геометрию, названную его именем. Аксиома Лобачевского гласит, что через точку, не лежащую на прямой можно провести более одной прямой, параллельной данной. Лобачевский, используя эту аксиому вместе с другими положениями, построил новую геометрию, которая в силу отсутствия наглядности, оставалась гипотетической до 1868 года, когда было дано её полное обоснование. Лобачевский, таким образом, открыл принципы построения новых геометрических теорий и способствовал развитию аксиоматического метода.

Следующим шагом явилось определение абстрактного математического пространства. Проективные, аффинные и конформные преобразования, сохраняющиеся при этом свойства фигур, привели к созданию проективной, аффинной и конформной геометрий. Переход от трёхмерного пространства к n-мерному впервые был осуществлён в работах Грассмана и Кэли в 1844 году и привёл к созданию многомерной геометрии. Другим обобщением пространства стала риманова геометрия, предложенная Риманом в 1854 году. Ф. Клейн в «Эрлангенской программе» систематизировал все виды однородных геометрий; согласно ему геометрия изучает все те свойства фигур, которые инвариантны относительно преобразований из некоторой группы. При этом каждая группа задаёт свою геометрию. Так, изометрии (движения) задаёт евклидову геометрию, группа аффинных преобразований — аффинную геометрию.

В 70-х годах XIX века возникла теория множеств, с точки зрения которой фигура определяется как множество точек. Данный подход позволил по новому взглянуть на евклидову геометрию и проанализировать её основы, которые подверглись некоторым уточнениям в работах Гильберта.

Геометрия в философии и искусстве

Со времён Древней Греции в основе геометрии лежат философские понятия. Определяя точку как «то, что не имеет частей», подход к ней отличается у Пифагора, который отождествляет точку с числовой единицей и у которого точка имеет только положение в пространстве и не имеет размера, и у Демокрита, который строя атомистическую теорию, даёт точке «сверхчувственно малый» размер. К атомистическим представлениям восходят также определения линии и поверхности, где неделимыми являются «ширина» и «глубина», соответственно.

Геометрия является пятым из семи свободных искусств по уровню обучения. Ей предшествует тривиум, состоящий из Грамматики, Риторики и Диалектики, а также Арифметика — старшая наука в квадривиуме, к которому также относятся Музыка и Астрономия. Марциан Капелла в своём трактате «Свадьба Философии и Меркурия» создал визуальные образы всех семи искусств и в том числе Геометрии. Искусства олицетворяли женщины с соответствующими атрибутами, которые сопровождались известными представителями сферы. Геометрия держит в своих руках глобус и циркуль, которым она может мерить, реже угольник, линейку или компасы. Её сопровождает Евклид.

В честь геометрии назван астероид (376) Геометрия, открытый в 1893 году.

Литература

• Комацу, Мацуо. Многообразие геометрии. — М. : Знание, 1981.</span>
• Левитин, К. Е. Геометрическая рапсодия. — 3-е изд., перераб. и доп. — М. : ИД «Камерон», 2004. — 216 с. — ISBN 5-9594-0023-5.</span>
• Шаль, Мишель. Исторический обзор происхождения и развития геометрических методов : в 2 т. — М. : М. Катков, 1883.</span>
• Геометрия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Геометрия // Газлифт — Гоголево. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 6).</span>
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1970. — Т. I : [ilib.mccme.ru/djvu/istoria/istmat1.htm С древнейших времён до начала Нового времени].</span>
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1970. — Т. II : [ilib.mccme.ru/djvu/istoria/istmat2.htm Математика XVII столетия].</span>
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1972. — Т. III : [ilib.mccme.ru/djvu/istoria/istmat3.htm Математика XVIII столетия].</span>
• Математика XIX века / ред. А. Н. Колмогоров, А. П. Юшкевич. — М. : Наука, 1981. — Т. 2 : [djvu.504.com1.ru:8019/WWW/2195fea01b9bd0b893a20ae895a6dc93.djvu Геометрия. Теория аналитических функций].</span>
• Энциклопедия элементарной математики / под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М. : Физматгиз, 1963. — Кн. 4 : [ilib.mccme.ru/djvu/encikl/enc-el-4.htm Геометрия]. — 568 с.</span>
• Энциклопедия элементарной математики / под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М. : Наука, 1966. — Кн. 5 : [ilib.mccme.ru/djvu/encikl/enc-el-5.htm Геометрия]. — 624 с.</span>

Математика

Отрывок, характеризующий Геометрия

– Ну, а остальных ты куда деваешь? – сказал Долохов.
– Как куда? Отсылаю под г'асписки! – вдруг покраснев, вскрикнул Денисов. – И смело скажу, что на моей совести нет ни одного человека. Разве тебе тг'удно отослать тг'идцать ли, тг'иста ли человек под конвоем в гог'од, чем маг'ать, я пг'ямо скажу, честь солдата.
– Вот молоденькому графчику в шестнадцать лет говорить эти любезности прилично, – с холодной усмешкой сказал Долохов, – а тебе то уж это оставить пора.
– Что ж, я ничего не говорю, я только говорю, что я непременно поеду с вами, – робко сказал Петя.
– А нам с тобой пора, брат, бросить эти любезности, – продолжал Долохов, как будто он находил особенное удовольствие говорить об этом предмете, раздражавшем Денисова. – Ну этого ты зачем взял к себе? – сказал он, покачивая головой. – Затем, что тебе его жалко? Ведь мы знаем эти твои расписки. Ты пошлешь их сто человек, а придут тридцать. Помрут с голоду или побьют. Так не все ли равно их и не брать?
Эсаул, щуря светлые глаза, одобрительно кивал головой.
– Это все г'авно, тут Рассуждать нечего. Я на свою душу взять не хочу. Ты говог'ишь – помг'ут. Ну, хог'ошо. Только бы не от меня.
Долохов засмеялся.
– Кто же им не велел меня двадцать раз поймать? А ведь поймают – меня и тебя, с твоим рыцарством, все равно на осинку. – Он помолчал. – Однако надо дело делать. Послать моего казака с вьюком! У меня два французских мундира. Что ж, едем со мной? – спросил он у Пети.
– Я? Да, да, непременно, – покраснев почти до слез, вскрикнул Петя, взглядывая на Денисова.
Опять в то время, как Долохов заспорил с Денисовым о том, что надо делать с пленными, Петя почувствовал неловкость и торопливость; но опять не успел понять хорошенько того, о чем они говорили. «Ежели так думают большие, известные, стало быть, так надо, стало быть, это хорошо, – думал он. – А главное, надо, чтобы Денисов не смел думать, что я послушаюсь его, что он может мной командовать. Непременно поеду с Долоховым во французский лагерь. Он может, и я могу».
На все убеждения Денисова не ездить Петя отвечал, что он тоже привык все делать аккуратно, а не наобум Лазаря, и что он об опасности себе никогда не думает.
– Потому что, – согласитесь сами, – если не знать верно, сколько там, от этого зависит жизнь, может быть, сотен, а тут мы одни, и потом мне очень этого хочется, и непременно, непременно поеду, вы уж меня не удержите, – говорил он, – только хуже будет…


Одевшись в французские шинели и кивера, Петя с Долоховым поехали на ту просеку, с которой Денисов смотрел на лагерь, и, выехав из леса в совершенной темноте, спустились в лощину. Съехав вниз, Долохов велел сопровождавшим его казакам дожидаться тут и поехал крупной рысью по дороге к мосту. Петя, замирая от волнения, ехал с ним рядом.
– Если попадемся, я живым не отдамся, у меня пистолет, – прошептал Петя.
– Не говори по русски, – быстрым шепотом сказал Долохов, и в ту же минуту в темноте послышался оклик: «Qui vive?» [Кто идет?] и звон ружья.
Кровь бросилась в лицо Пети, и он схватился за пистолет.
– Lanciers du sixieme, [Уланы шестого полка.] – проговорил Долохов, не укорачивая и не прибавляя хода лошади. Черная фигура часового стояла на мосту.
– Mot d'ordre? [Отзыв?] – Долохов придержал лошадь и поехал шагом.
– Dites donc, le colonel Gerard est ici? [Скажи, здесь ли полковник Жерар?] – сказал он.
– Mot d'ordre! – не отвечая, сказал часовой, загораживая дорогу.
– Quand un officier fait sa ronde, les sentinelles ne demandent pas le mot d'ordre… – крикнул Долохов, вдруг вспыхнув, наезжая лошадью на часового. – Je vous demande si le colonel est ici? [Когда офицер объезжает цепь, часовые не спрашивают отзыва… Я спрашиваю, тут ли полковник?]
И, не дожидаясь ответа от посторонившегося часового, Долохов шагом поехал в гору.
Заметив черную тень человека, переходящего через дорогу, Долохов остановил этого человека и спросил, где командир и офицеры? Человек этот, с мешком на плече, солдат, остановился, близко подошел к лошади Долохова, дотрогиваясь до нее рукою, и просто и дружелюбно рассказал, что командир и офицеры были выше на горе, с правой стороны, на дворе фермы (так он называл господскую усадьбу).
Проехав по дороге, с обеих сторон которой звучал от костров французский говор, Долохов повернул во двор господского дома. Проехав в ворота, он слез с лошади и подошел к большому пылавшему костру, вокруг которого, громко разговаривая, сидело несколько человек. В котелке с краю варилось что то, и солдат в колпаке и синей шинели, стоя на коленях, ярко освещенный огнем, мешал в нем шомполом.
– Oh, c'est un dur a cuire, [С этим чертом не сладишь.] – говорил один из офицеров, сидевших в тени с противоположной стороны костра.
– Il les fera marcher les lapins… [Он их проберет…] – со смехом сказал другой. Оба замолкли, вглядываясь в темноту на звук шагов Долохова и Пети, подходивших к костру с своими лошадьми.
– Bonjour, messieurs! [Здравствуйте, господа!] – громко, отчетливо выговорил Долохов.
Офицеры зашевелились в тени костра, и один, высокий офицер с длинной шеей, обойдя огонь, подошел к Долохову.
– C'est vous, Clement? – сказал он. – D'ou, diable… [Это вы, Клеман? Откуда, черт…] – но он не докончил, узнав свою ошибку, и, слегка нахмурившись, как с незнакомым, поздоровался с Долоховым, спрашивая его, чем он может служить. Долохов рассказал, что он с товарищем догонял свой полк, и спросил, обращаясь ко всем вообще, не знали ли офицеры чего нибудь о шестом полку. Никто ничего не знал; и Пете показалось, что офицеры враждебно и подозрительно стали осматривать его и Долохова. Несколько секунд все молчали.
– Si vous comptez sur la soupe du soir, vous venez trop tard, [Если вы рассчитываете на ужин, то вы опоздали.] – сказал с сдержанным смехом голос из за костра.
Долохов отвечал, что они сыты и что им надо в ночь же ехать дальше.
Он отдал лошадей солдату, мешавшему в котелке, и на корточках присел у костра рядом с офицером с длинной шеей. Офицер этот, не спуская глаз, смотрел на Долохова и переспросил его еще раз: какого он был полка? Долохов не отвечал, как будто не слыхал вопроса, и, закуривая коротенькую французскую трубку, которую он достал из кармана, спрашивал офицеров о том, в какой степени безопасна дорога от казаков впереди их.
– Les brigands sont partout, [Эти разбойники везде.] – отвечал офицер из за костра.
Долохов сказал, что казаки страшны только для таких отсталых, как он с товарищем, но что на большие отряды казаки, вероятно, не смеют нападать, прибавил он вопросительно. Никто ничего не ответил.
«Ну, теперь он уедет», – всякую минуту думал Петя, стоя перед костром и слушая его разговор.
Но Долохов начал опять прекратившийся разговор и прямо стал расспрашивать, сколько у них людей в батальоне, сколько батальонов, сколько пленных. Спрашивая про пленных русских, которые были при их отряде, Долохов сказал:
– La vilaine affaire de trainer ces cadavres apres soi. Vaudrait mieux fusiller cette canaille, [Скверное дело таскать за собой эти трупы. Лучше бы расстрелять эту сволочь.] – и громко засмеялся таким странным смехом, что Пете показалось, французы сейчас узнают обман, и он невольно отступил на шаг от костра. Никто не ответил на слова и смех Долохова, и французский офицер, которого не видно было (он лежал, укутавшись шинелью), приподнялся и прошептал что то товарищу. Долохов встал и кликнул солдата с лошадьми.
«Подадут или нет лошадей?» – думал Петя, невольно приближаясь к Долохову.
Лошадей подали.
– Bonjour, messieurs, [Здесь: прощайте, господа.] – сказал Долохов.
Петя хотел сказать bonsoir [добрый вечер] и не мог договорить слова. Офицеры что то шепотом говорили между собою. Долохов долго садился на лошадь, которая не стояла; потом шагом поехал из ворот. Петя ехал подле него, желая и не смея оглянуться, чтоб увидать, бегут или не бегут за ними французы.
Выехав на дорогу, Долохов поехал не назад в поле, а вдоль по деревне. В одном месте он остановился, прислушиваясь.
– Слышишь? – сказал он.
Петя узнал звуки русских голосов, увидал у костров темные фигуры русских пленных. Спустившись вниз к мосту, Петя с Долоховым проехали часового, который, ни слова не сказав, мрачно ходил по мосту, и выехали в лощину, где дожидались казаки.
– Ну, теперь прощай. Скажи Денисову, что на заре, по первому выстрелу, – сказал Долохов и хотел ехать, но Петя схватился за него рукою.
– Нет! – вскрикнул он, – вы такой герой. Ах, как хорошо! Как отлично! Как я вас люблю.
– Хорошо, хорошо, – сказал Долохов, но Петя не отпускал его, и в темноте Долохов рассмотрел, что Петя нагибался к нему. Он хотел поцеловаться. Долохов поцеловал его, засмеялся и, повернув лошадь, скрылся в темноте.

Х
Вернувшись к караулке, Петя застал Денисова в сенях. Денисов в волнении, беспокойстве и досаде на себя, что отпустил Петю, ожидал его.
– Слава богу! – крикнул он. – Ну, слава богу! – повторял он, слушая восторженный рассказ Пети. – И чег'т тебя возьми, из за тебя не спал! – проговорил Денисов. – Ну, слава богу, тепег'ь ложись спать. Еще вздг'емнем до утг'а.
– Да… Нет, – сказал Петя. – Мне еще не хочется спать. Да я и себя знаю, ежели засну, так уж кончено. И потом я привык не спать перед сражением.
Петя посидел несколько времени в избе, радостно вспоминая подробности своей поездки и живо представляя себе то, что будет завтра. Потом, заметив, что Денисов заснул, он встал и пошел на двор.
На дворе еще было совсем темно. Дождик прошел, но капли еще падали с деревьев. Вблизи от караулки виднелись черные фигуры казачьих шалашей и связанных вместе лошадей. За избушкой чернелись две фуры, у которых стояли лошади, и в овраге краснелся догоравший огонь. Казаки и гусары не все спали: кое где слышались, вместе с звуком падающих капель и близкого звука жевания лошадей, негромкие, как бы шепчущиеся голоса.
Петя вышел из сеней, огляделся в темноте и подошел к фурам. Под фурами храпел кто то, и вокруг них стояли, жуя овес, оседланные лошади. В темноте Петя узнал свою лошадь, которую он называл Карабахом, хотя она была малороссийская лошадь, и подошел к ней.
– Ну, Карабах, завтра послужим, – сказал он, нюхая ее ноздри и целуя ее.
– Что, барин, не спите? – сказал казак, сидевший под фурой.
– Нет; а… Лихачев, кажется, тебя звать? Ведь я сейчас только приехал. Мы ездили к французам. – И Петя подробно рассказал казаку не только свою поездку, но и то, почему он ездил и почему он считает, что лучше рисковать своей жизнью, чем делать наобум Лазаря.
– Что же, соснули бы, – сказал казак.
– Нет, я привык, – отвечал Петя. – А что, у вас кремни в пистолетах не обились? Я привез с собою. Не нужно ли? Ты возьми.
Казак высунулся из под фуры, чтобы поближе рассмотреть Петю.
– Оттого, что я привык все делать аккуратно, – сказал Петя. – Иные так, кое как, не приготовятся, потом и жалеют. Я так не люблю.
– Это точно, – сказал казак.
– Да еще вот что, пожалуйста, голубчик, наточи мне саблю; затупи… (но Петя боялся солгать) она никогда отточена не была. Можно это сделать?
– Отчего ж, можно.
Лихачев встал, порылся в вьюках, и Петя скоро услыхал воинственный звук стали о брусок. Он влез на фуру и сел на край ее. Казак под фурой точил саблю.
– А что же, спят молодцы? – сказал Петя.
– Кто спит, а кто так вот.
– Ну, а мальчик что?
– Весенний то? Он там, в сенцах, завалился. Со страху спится. Уж рад то был.
Долго после этого Петя молчал, прислушиваясь к звукам. В темноте послышались шаги и показалась черная фигура.
– Что точишь? – спросил человек, подходя к фуре.
– А вот барину наточить саблю.
– Хорошее дело, – сказал человек, который показался Пете гусаром. – У вас, что ли, чашка осталась?
– А вон у колеса.
Гусар взял чашку.
– Небось скоро свет, – проговорил он, зевая, и прошел куда то.
Петя должен бы был знать, что он в лесу, в партии Денисова, в версте от дороги, что он сидит на фуре, отбитой у французов, около которой привязаны лошади, что под ним сидит казак Лихачев и натачивает ему саблю, что большое черное пятно направо – караулка, и красное яркое пятно внизу налево – догоравший костер, что человек, приходивший за чашкой, – гусар, который хотел пить; но он ничего не знал и не хотел знать этого. Он был в волшебном царстве, в котором ничего не было похожего на действительность. Большое черное пятно, может быть, точно была караулка, а может быть, была пещера, которая вела в самую глубь земли. Красное пятно, может быть, был огонь, а может быть – глаз огромного чудовища. Может быть, он точно сидит теперь на фуре, а очень может быть, что он сидит не на фуре, а на страшно высокой башне, с которой ежели упасть, то лететь бы до земли целый день, целый месяц – все лететь и никогда не долетишь. Может быть, что под фурой сидит просто казак Лихачев, а очень может быть, что это – самый добрый, храбрый, самый чудесный, самый превосходный человек на свете, которого никто не знает. Может быть, это точно проходил гусар за водой и пошел в лощину, а может быть, он только что исчез из виду и совсем исчез, и его не было.
Что бы ни увидал теперь Петя, ничто бы не удивило его. Он был в волшебном царстве, в котором все было возможно.
Он поглядел на небо. И небо было такое же волшебное, как и земля. На небе расчищало, и над вершинами дерев быстро бежали облака, как будто открывая звезды. Иногда казалось, что на небе расчищало и показывалось черное, чистое небо. Иногда казалось, что эти черные пятна были тучки. Иногда казалось, что небо высоко, высоко поднимается над головой; иногда небо спускалось совсем, так что рукой можно было достать его.
Петя стал закрывать глаза и покачиваться.
Капли капали. Шел тихий говор. Лошади заржали и подрались. Храпел кто то.
– Ожиг, жиг, ожиг, жиг… – свистела натачиваемая сабля. И вдруг Петя услыхал стройный хор музыки, игравшей какой то неизвестный, торжественно сладкий гимн. Петя был музыкален, так же как Наташа, и больше Николая, но он никогда не учился музыке, не думал о музыке, и потому мотивы, неожиданно приходившие ему в голову, были для него особенно новы и привлекательны. Музыка играла все слышнее и слышнее. Напев разрастался, переходил из одного инструмента в другой. Происходило то, что называется фугой, хотя Петя не имел ни малейшего понятия о том, что такое фуга. Каждый инструмент, то похожий на скрипку, то на трубы – но лучше и чище, чем скрипки и трубы, – каждый инструмент играл свое и, не доиграв еще мотива, сливался с другим, начинавшим почти то же, и с третьим, и с четвертым, и все они сливались в одно и опять разбегались, и опять сливались то в торжественно церковное, то в ярко блестящее и победное.
«Ах, да, ведь это я во сне, – качнувшись наперед, сказал себе Петя. – Это у меня в ушах. А может быть, это моя музыка. Ну, опять. Валяй моя музыка! Ну!..»
Он закрыл глаза. И с разных сторон, как будто издалека, затрепетали звуки, стали слаживаться, разбегаться, сливаться, и опять все соединилось в тот же сладкий и торжественный гимн. «Ах, это прелесть что такое! Сколько хочу и как хочу», – сказал себе Петя. Он попробовал руководить этим огромным хором инструментов.
«Ну, тише, тише, замирайте теперь. – И звуки слушались его. – Ну, теперь полнее, веселее. Еще, еще радостнее. – И из неизвестной глубины поднимались усиливающиеся, торжественные звуки. – Ну, голоса, приставайте!» – приказал Петя. И сначала издалека послышались голоса мужские, потом женские. Голоса росли, росли в равномерном торжественном усилии. Пете страшно и радостно было внимать их необычайной красоте.
С торжественным победным маршем сливалась песня, и капли капали, и вжиг, жиг, жиг… свистела сабля, и опять подрались и заржали лошади, не нарушая хора, а входя в него.
Петя не знал, как долго это продолжалось: он наслаждался, все время удивлялся своему наслаждению и жалел, что некому сообщить его. Его разбудил ласковый голос Лихачева.
– Готово, ваше благородие, надвое хранцуза распластаете.
Петя очнулся.
– Уж светает, право, светает! – вскрикнул он.
Невидные прежде лошади стали видны до хвостов, и сквозь оголенные ветки виднелся водянистый свет. Петя встряхнулся, вскочил, достал из кармана целковый и дал Лихачеву, махнув, попробовал шашку и положил ее в ножны. Казаки отвязывали лошадей и подтягивали подпруги.
– Вот и командир, – сказал Лихачев. Из караулки вышел Денисов и, окликнув Петю, приказал собираться.


Быстро в полутьме разобрали лошадей, подтянули подпруги и разобрались по командам. Денисов стоял у караулки, отдавая последние приказания. Пехота партии, шлепая сотней ног, прошла вперед по дороге и быстро скрылась между деревьев в предрассветном тумане. Эсаул что то приказывал казакам. Петя держал свою лошадь в поводу, с нетерпением ожидая приказания садиться. Обмытое холодной водой, лицо его, в особенности глаза горели огнем, озноб пробегал по спине, и во всем теле что то быстро и равномерно дрожало.
– Ну, готово у вас все? – сказал Денисов. – Давай лошадей.
Лошадей подали. Денисов рассердился на казака за то, что подпруги были слабы, и, разбранив его, сел. Петя взялся за стремя. Лошадь, по привычке, хотела куснуть его за ногу, но Петя, не чувствуя своей тяжести, быстро вскочил в седло и, оглядываясь на тронувшихся сзади в темноте гусар, подъехал к Денисову.
– Василий Федорович, вы мне поручите что нибудь? Пожалуйста… ради бога… – сказал он. Денисов, казалось, забыл про существование Пети. Он оглянулся на него.
– Об одном тебя пг'ошу, – сказал он строго, – слушаться меня и никуда не соваться.
Во все время переезда Денисов ни слова не говорил больше с Петей и ехал молча. Когда подъехали к опушке леса, в поле заметно уже стало светлеть. Денисов поговорил что то шепотом с эсаулом, и казаки стали проезжать мимо Пети и Денисова. Когда они все проехали, Денисов тронул свою лошадь и поехал под гору. Садясь на зады и скользя, лошади спускались с своими седоками в лощину. Петя ехал рядом с Денисовым. Дрожь во всем его теле все усиливалась. Становилось все светлее и светлее, только туман скрывал отдаленные предметы. Съехав вниз и оглянувшись назад, Денисов кивнул головой казаку, стоявшему подле него.
– Сигнал! – проговорил он.
Казак поднял руку, раздался выстрел. И в то же мгновение послышался топот впереди поскакавших лошадей, крики с разных сторон и еще выстрелы.
В то же мгновение, как раздались первые звуки топота и крика, Петя, ударив свою лошадь и выпустив поводья, не слушая Денисова, кричавшего на него, поскакал вперед. Пете показалось, что вдруг совершенно, как середь дня, ярко рассвело в ту минуту, как послышался выстрел. Он подскакал к мосту. Впереди по дороге скакали казаки. На мосту он столкнулся с отставшим казаком и поскакал дальше. Впереди какие то люди, – должно быть, это были французы, – бежали с правой стороны дороги на левую. Один упал в грязь под ногами Петиной лошади.
У одной избы столпились казаки, что то делая. Из середины толпы послышался страшный крик. Петя подскакал к этой толпе, и первое, что он увидал, было бледное, с трясущейся нижней челюстью лицо француза, державшегося за древко направленной на него пики.
– Ура!.. Ребята… наши… – прокричал Петя и, дав поводья разгорячившейся лошади, поскакал вперед по улице.
Впереди слышны были выстрелы. Казаки, гусары и русские оборванные пленные, бежавшие с обеих сторон дороги, все громко и нескладно кричали что то. Молодцеватый, без шапки, с красным нахмуренным лицом, француз в синей шинели отбивался штыком от гусаров. Когда Петя подскакал, француз уже упал. Опять опоздал, мелькнуло в голове Пети, и он поскакал туда, откуда слышались частые выстрелы. Выстрелы раздавались на дворе того барского дома, на котором он был вчера ночью с Долоховым. Французы засели там за плетнем в густом, заросшем кустами саду и стреляли по казакам, столпившимся у ворот. Подъезжая к воротам, Петя в пороховом дыму увидал Долохова с бледным, зеленоватым лицом, кричавшего что то людям. «В объезд! Пехоту подождать!» – кричал он, в то время как Петя подъехал к нему.
– Подождать?.. Ураааа!.. – закричал Петя и, не медля ни одной минуты, поскакал к тому месту, откуда слышались выстрелы и где гуще был пороховой дым. Послышался залп, провизжали пустые и во что то шлепнувшие пули. Казаки и Долохов вскакали вслед за Петей в ворота дома. Французы в колеблющемся густом дыме одни бросали оружие и выбегали из кустов навстречу казакам, другие бежали под гору к пруду. Петя скакал на своей лошади вдоль по барскому двору и, вместо того чтобы держать поводья, странно и быстро махал обеими руками и все дальше и дальше сбивался с седла на одну сторону. Лошадь, набежав на тлевший в утреннем свето костер, уперлась, и Петя тяжело упал на мокрую землю. Казаки видели, как быстро задергались его руки и ноги, несмотря на то, что голова его не шевелилась. Пуля пробила ему голову.
Переговоривши с старшим французским офицером, который вышел к нему из за дома с платком на шпаге и объявил, что они сдаются, Долохов слез с лошади и подошел к неподвижно, с раскинутыми руками, лежавшему Пете.
– Готов, – сказал он, нахмурившись, и пошел в ворота навстречу ехавшему к нему Денисову.
– Убит?! – вскрикнул Денисов, увидав еще издалека то знакомое ему, несомненно безжизненное положение, в котором лежало тело Пети.
– Готов, – повторил Долохов, как будто выговаривание этого слова доставляло ему удовольствие, и быстро пошел к пленным, которых окружили спешившиеся казаки. – Брать не будем! – крикнул он Денисову.
Денисов не отвечал; он подъехал к Пете, слез с лошади и дрожащими руками повернул к себе запачканное кровью и грязью, уже побледневшее лицо Пети.
«Я привык что нибудь сладкое. Отличный изюм, берите весь», – вспомнилось ему. И казаки с удивлением оглянулись на звуки, похожие на собачий лай, с которыми Денисов быстро отвернулся, подошел к плетню и схватился за него.
В числе отбитых Денисовым и Долоховым русских пленных был Пьер Безухов.


О той партии пленных, в которой был Пьер, во время всего своего движения от Москвы, не было от французского начальства никакого нового распоряжения. Партия эта 22 го октября находилась уже не с теми войсками и обозами, с которыми она вышла из Москвы. Половина обоза с сухарями, который шел за ними первые переходы, была отбита казаками, другая половина уехала вперед; пеших кавалеристов, которые шли впереди, не было ни одного больше; они все исчезли. Артиллерия, которая первые переходы виднелась впереди, заменилась теперь огромным обозом маршала Жюно, конвоируемого вестфальцами. Сзади пленных ехал обоз кавалерийских вещей.