Задача о разорении игрока
Задача о разорении игрока — задача из области теории вероятностей. Подробно рассматривалась российским математиком А. Н. Ширяевым в монографии «Вероятность»[1].

Содержание
Формулировка
За столом сидят два игрока. У первого в распоряжении находится <math>-A\ (A<0, -A>0)</math> рублей, у второго в распоряжении находится <math>B\ (B>0)</math> рублей. Перед ними на столе лежит асимметричная монета (вероятность, что выпадет аверс, может равняться любому числу от 0 до 1 включительно). Если на монете выпадает аверс, то рубль выигрывает первый игрок (второй игрок выплачивает первому 1 рубль), а если выпадает реверс, то первый игрок платит второму один рубль. Требуется найти вероятность того, что один из игроков проиграется в ноль за <math>n</math> шагов, и вероятность проигрыша каждого азартного игрока. Также необходимо вычислить среднюю длину игры.
Данная ситуация может быть смоделирована подобным образом: имеется блуждающая частица и коридор <math>[A;B]</math>. Рассматривается вероятность того, что частица выйдет из коридора за <math>n</math> шагов (проскочит через верхнюю или нижнюю стенку).
Схема Бернулли
Рассмотрим схему Бернулли с <math>n</math> испытаниями. Пусть <math>(\Omega,\mathcal{A},\mathbb{P})</math> — вероятностное пространство, где <math>\Omega = \bigl\{\omega\colon \omega=(x_1;\ldots;x_n),\ x_i = \pm 1 \bigr\}</math>. <math>\mathcal{A} = \{ A_i \subseteq \Omega \}</math> — алгебра подмножеств вероятностного пространства. Вероятность задана следующим образом: <math>\mathbb{P}\bigl(\{ \omega \}\bigr) = p^{\nu(\omega)}\cdot q^{n-\nu(\omega)}</math>, где <math>\nu(\omega)</math> — количество выпавших в данной последовательность единиц: <math>\nu(\omega) = \frac{\sum\limits_{i=1}^n x_i + n}{2}</math>. Данная формула позволяет считать количество единиц: <math>\nu(\omega)</math> превращает соответственно полученные значения <math>(+1;-1)</math> в <math>(1;0)</math> и затем уже считает полученные единицы. Введём последовательность бернуллиевских случайных величин <math>\xi_i(\omega)\colon i=\overline{1;n};\quad\mathbb{P}\bigl(\{\xi_i=1\}\bigr)=p;\quad\mathbb{P}\bigl(\{\xi_i=-1\}\bigr)=q;\quad p+q=1.</math>
Подзадача о нормированности вероятности
Доказать, что <math>\sum\limits_{\omega\in\Omega} \mathbb{P}\bigl(\{\omega\}\bigr) = 1.</math>
Решение. <math>\sum\limits_{\omega\in\Omega} \mathbb{P}\bigl(\{\omega\}\bigr) = \sum\limits_{\omega\in\Omega} p^{\frac{\sum\limits_{i=1}^n x_i + n}{2}} \cdot q^{n-\frac{\sum\limits_{i=1}^n x_i + n}{2}} = \sum\limits_{k=0}^n \sum\limits_{\omega\in A_k} p^{\frac{\sum\limits_{i=1}^n (x_i+1)}{2}} \cdot q^{\frac{\sum\limits_{i=1}^n (1-x_i)}{2}} = \sum\limits_{k=0}^n C^k_n p^k q^{n-k}.</math> Это справедливо в силу того, что <math>\frac{x_i+1}{2}\in \{ 0;1 \}.</math> <math>\sum\limits_{k=0}^n C^k_n p^k q^{n-k} = (p+q)^n = 1</math>, поскольку по условию <math>p+q=1</math>. <math>\blacksquare</math>
Подзадача о независимости случайных величин <math>\xi_i</math>
Доказать, что <math>\xi_1</math> и <math>\xi_2</math> независимы.
Решение. Достаточно доказать, что <math>\mathbb{P}\bigl(\{\xi_1=1\}\cap\{\xi_2=1\} \bigr)=\mathbb{P}\bigl( \{\xi_1=1\} \bigr)\mathbb{P} \bigl(\{\xi_2=1\} \bigr).</math>
| <math>\mathbb{P}\bigl( \{\xi_1=1\}\cap\{\xi_2=1\} \bigr) = \mathbb{P} \bigl(\{ \omega\colon \omega=(x_1;\ldots;x_n),\ x_1=1,\ x_2=1 \} \bigr) = </math> |
| <math>=\sum\limits_{\begin{smallmatrix}x_3=\pm 1 \\ \ldots{} \\ x_n=\pm 1\end{smallmatrix}} p^{\frac{2+\sum\limits_{i=3}^n x_i + n}{2}}\cdot q^{n - \frac{2+\sum\limits_{i=3}^n x_i + n}{2}} =
p^2 \sum\limits_{\begin{smallmatrix}x_3=\pm 1 \\ \ldots{} \\ x_n=\pm 1\end{smallmatrix}} p^{\frac{\sum\limits_{i=3}^n x_i + (n-2)}{2}}\cdot q^{(n-2) - \frac{\sum\limits_{i=3}^n x_i + (n-2)}{2}} = p^2 \cdot 1.</math> <math>\blacksquare</math> |
Случайное блуждание
Введём новое обозначение: <math>S_0 = 0</math>, <math>S_k = \xi_1 + \ldots{} + \xi_k, \quad 1\leqslant k \leqslant n</math>. <math>n</math> — длина игры, а последовательность <math>(S_k)_{k\leqslant n}</math> можно рассматривать как траекторию случайного блуждания некоторой частицы, выходящей из нуля. При этом <math>S_{k+1} = S_k + \xi_{k+1}</math>. Пусть <math>A</math>, <math>B</math> — два целых числа, <math>A\leqslant 0</math>, <math>B \geqslant 0</math>. Требуется найти, с какой вероятностью за <math>n</math> шагов будет осуществлён выход частицы из коридора, ограниченного <math>A</math> и <math>B</math>. Если <math>\xi_i = +1</math>, то второй игрок платит первому. Если <math>\xi_i = -1</math>, то первый игрок платит второму. Поэтому <math>S_k</math> может рассматриваться в качестве выигрыша первого игрока у второго (который, естественно, может быть отрицательным). Далее, пусть <math>x</math> — целое число, <math>x\in \mathbb{Z}\cap [A;B]</math>. Пусть также для <math>0\leqslant k \leqslant n</math> верно, что <math>S^x_k = x+S_k</math> (что означает, что игроки начинали играть с ненулевым капиталом в распоряжении). Пусть <math>\tau^x_k = \min \bigl\{ l\colon 0\leqslant l \leqslant k, S^x_l = \{A \mathrm{~or~} B \} \bigr\}</math>. Условимся считать, что <math>\tau^x_k = k</math>, если <math>A < S_l^x < B\quad \forall l\colon 0\leqslant l \leqslant k</math>. Если частица так и не пересекла границы, то <math>x_k</math> не определён.
Для каждого <math>0\leqslant k \leqslant n</math> и <math>x\in [A; B]\cap \mathbb{Z}</math> момент <math>\tau^x_k</math> называется моментом остановки, который является случайной величиной, определённой на пространстве элементарных событий <math>\Omega</math>. <math>\forall l<k\quad \{\omega\colon \tau^x_k = l\}</math> — это событие, состоящее в том, что случайное блуждание <math>\{S^x_i\colon 0\leqslant i \leqslant k \}</math>, начинающееся в точке <math>x</math>, выйдет из интервала <math>[A;B]</math> в момент <math>l</math>. Введём новые обозначения: <math>\mathcal{A}^x_k = \coprod\limits_{0\leqslant l \leqslant k}\{ \omega\colon \tau^x_k= l, \ S^x_l = A \}</math>, <math>\mathcal{B}^x_k = \coprod\limits_{0\leqslant l \leqslant k}\{ \omega\colon \tau^x_k= l, \ S^x_l = B \}</math> для <math>0\leqslant k \leqslant n</math>. Пусть <math>\alpha_k(x) = \mathbb{P} (\mathcal{A}^x_k)</math>, <math>\beta_k(x) = \mathbb{P} (\mathcal{B}^x_k)</math> — вероятности выхода частицы за время <math>[0;k]</math> из интервала <math>[A;B]</math> соответственно в точках <math>A</math> и <math>B</math>.
Пусть <math>A<x<B</math>; очевидно, что <math>\alpha_0(x) = \beta_0 (x) = 0</math> (пока игра не началась, частица находится внутри интервала с вероятностью 1). Пусть теперь <math>0\leqslant k \leqslant n</math>. Тогда по формуле полной вероятности <math>\beta_k (x) = \mathbb{P} (\mathcal{B}^x_k) = \mathbb{P} ( \mathcal{B}^x_k \mid S_1^x = x+1 )\cdot \mathbb{P}\bigl(\{\xi_1 = 1 \}\bigr) + \mathbb{P} ( \mathcal{B}^x_k \mid S_1^x = x-1 )\cdot \mathbb{P}\bigl(\{ \xi_1 = -1 \}\bigr).</math>
Подзадача о рекуррентности
Доказать, что (1) <math>\mathbb{P} ( \mathcal{B}^x_k \mid S_1^x = x+1 ) = \mathbb{P} ( \mathcal{B}^{x+1}_{k-1} )</math> и (2) <math>\mathbb{P} ( \mathcal{B}^x_k \mid S_1^x = x-1 ) = \mathbb{P} ( \mathcal{B}^{x-1}_{k-1} )</math>.
Доказательство.
(1) Докажем, что <math>\mathbb{P} ( \mathcal{B}^x_k \mid S_1^x = x+1 ) = \mathbb{P} ( \mathcal{B}^{x+1}_{k-1} )</math>. <math>\mathcal{B}^x_k = \bigl\{ \omega\colon (x;x+\xi_1;\ldots{};x+\xi_1+\ldots{}+\xi_k) \in B^x_k \bigr\}</math>, где <math>B^x_k</math> — множество траекторий вида <math>(x;x+x_1;\ldots{};x+x_1+\ldots{}+x_k),\quad x_i=\pm 1</math>, которые за время <math>[0;k]</math> впервые выходят из интервала <math>(A;B)</math> в точке <math>B</math> (показано на рисунке). Если случайный вектор попадает в подходящую траекторию, то он попадает в множество <math>\mathcal{B}</math>. Представим множество <math>B_k^x</math> как <math>B_k^{x;x+1}\sqcup B_k^{x;x-1}</math>. Дизъюнктное объединение правомерно по причине того, что у любой частицы, проходящей по траектории, <math>x_1=\pm 1</math>. <math>B_k^{x;x+1}</math> — те траектории из <math>B_k^x</math>, для которых <math>x_1=1</math>. <math>B_k^{x;x-1}</math> — те траектории из <math>B_k^x</math>, для которых <math>x_1=-1</math>. Заметим, что каждая траектория <math>(x;x+1;x+1+x_2;\ldots{};x+1+x_2+\ldots+x_k)</math> из <math>B_k^{x;x+1}</math> находится в однозначном соответствии с траекторией <math>(x+1;x+1+x_2;\ldots{};x+1+x_2+\ldots+x_k)</math> из <math>B_{k-1}^{x+1}</math>. Взаимно-однозначное соответствие доказывается от противного. Предположим, что <math>x_1 = -1</math> (неоднозначное соответствие); тогда данная траектория <math>(x;x-1;x-1+x_2;\ldots;x-1+x_2+\ldots+x_k)</math> не сможет вывести частицу из коридора за <math>k</math> шагов (а только лишь за <math>k+2</math> из-за изначального отдаления от верхней стенки коридора). В обратную сторону соответствие является также однозначным из определения: <math>S_{k+1} = S_k + \xi_{k+1}</math>. Из этого следует, что <math>\mathbb{P} \Bigl(\big\{ (x+1;x+1+x_2;\ldots; x+1+x_2+\ldots+x_k) \in B_{k-1}^{x+1} \bigr\} \Bigr) = \mathbb{P} \Bigl( \bigl\{ (x+1;x+1+x_1;\ldots; x+1+x_1+\ldots+x_{k-1}) \in B_{k-1}^{x+1} \bigr\} \Bigr) \mathrel{\stackrel{\rm def}=} \mathbb{P}(\mathcal{B}_{k-1}^{x+1})</math> (так как <math>\xi_i</math> суть независимые одинаково распределённые случайные величины).
Существует и другой способ доказательства:
| <math>\mathbb{P} ( \mathcal{B}^x_k \mid S_1^x = x+1 ) = \mathbb{P} ( \mathcal{B}^x_k \mid \xi_1 = 1 ) = \mathbb{P} \bigl( (x;x+\xi_1;\ldots{};x+\xi_1+\ldots{}+\xi_k)\in B^x_k \mid \xi_1 = 1 \bigr) = </math> |
| <math>=\frac{\mathbb{P} \bigl( (x;x+\xi_1;\ldots{};x+\xi_1+\ldots{}+\xi_k)\in B^x_k \cap \xi_1 = 1 \bigr)}{\mathbb{P}(\{ \xi_1 = 1 \})} = \frac{\mathbb{P} \bigl( (x;x+1;\ldots{};x+1+\ldots{}+\xi_k)\in B^x_k \cap \xi_1 = 1 \bigr)}{\mathbb{P}(\{ \xi_1 = 1 \})} =</math> |
| <math>=\mathbb{P}\bigl( \{ (x;x+1;x+1+\xi_2;\ldots{};x+1+\xi_2+\ldots{}+\xi_k)\in B_k^x \} \bigr) = \mathbb{P}\bigl( \{ (x;x+1;x+1+\xi_1;\ldots{};x+1+\xi_1+\ldots{}+\xi_{k-1})\in B_k^x \} \bigr) =</math> |
| <math>=\mathbb{P}\bigl( \{ (x;x+1;x+1+\xi_1;\ldots{};x+1+\xi_1+\ldots{}+\xi_{k-1})\in B_{k-1}^{x+1} \} \bigr) =
\mathbb{P} (\mathcal{B}_{k-1}^{x+1}) = \beta_{k-1}(x+1)</math>. |
Это справедливо потому, что вероятности независимы (это было доказано ранее).
(2) Аналогично докажем, что <math>\mathbb{P} ( \mathcal{B}^x_k \mid S_1^x = x-1 ) = \mathbb{P} ( \mathcal{B}^{x+1}_{k-1} )</math>. Каждая траектория <math>(x;x-1;x-1+x_2;\ldots{};x-1+x_2+\ldots+x_k)</math> из <math>B_k^{x;x+1}</math> находится в однозначном соответствии с траекторией <math>(x-1;x-1+x_2;\ldots{};x-1+x_2+\ldots+x_k)</math> из <math>B_{k-1}^{x-1}</math>. Отсюда <math>\mathbb{P} \Bigl( \bigl\{ (x-1;x-1+x_2;\ldots; x-1+x_2+\ldots+x_k) \in B_{k-1}^{x-1} \bigr\} \Bigr) = \mathbb{P} \Bigl( \bigl\{ (x-1;x-1+x_1;\ldots; x-1+x_1+\ldots+x_{k-1}) \in B_{k-1}^{x-1} \bigr\} \Bigr) \mathrel{\stackrel{\rm def}=} \mathbb{P}(\mathcal{B}_{k-1}^{x-1}).</math> <math>\blacksquare</math>
Вывод рекуррентного соотношения
Из уравнения для <math>\beta_k(x)</math> следует, что для <math>x\in (A;B)</math> и <math>k\leqslant n</math> верно: <math>\mathbb{P}(\mathcal{B}_k^x) = \mathbb{P} ( \mathcal{B}^x_k \mid S_1^x = x+1 )\cdot p + \mathbb{P} ( \mathcal{B}^x_k \mid S_1^x = x-1 )\cdot q = \mathbb{P} ( \mathcal{B}^{x+1}_{k-1}) \cdot p + \mathbb{P} ( \mathcal{B}^{x-1}_{k-1})\cdot q = p\beta_{k-1}(x+1) + q\beta_{k-1}(x-1).</math>
<math>\beta_l(B)= 1</math>, <math>\beta_l(A)=0</math> для <math>l\in[0;n]</math>. Формула полной вероятности также даёт нам следующий результат: <math>\alpha_k(x) = p\alpha_{k-1}(x+1) + q\alpha_{k-1}(x-1)</math>. Также отметим, что <math>\mathcal{B}_{k-1} \subset \mathcal{B}_{k}</math>, и поэтому <math>\beta_{k-1}(x)\leqslant \beta_k(x)\leqslant 1</math> для <math>k \leqslant n</math>. Это утверждение верно, так как к любой траектории, выводящей частицу за меньшее количество шагов, можно прибавить в начало один шаг (<math>x_{j-1}=\pm 1</math>), на котором частица может прийти в точку <math>(j;S^x_{j})</math> как из <math>(j-1;S^x_{j}-1)</math> (для <math>\xi_j=1</math>), так и из <math>(j-1;S^x_{j}+1)</math> (<math>j\leqslant k</math>).
Нахождение вероятностей
При достаточно больших <math>n</math> вероятность <math>\beta_n (x)</math> близка к <math>\beta(x)</math> — решению уравнения <math>\beta(x) = p\beta(x+1) + q\beta(x-1)</math> при тех условиях, что <math>\beta(B)=1</math> (выход произошёл сразу же из точки <math>B</math> — конец игры, выиграл первый игрок), <math>\beta(A)=0</math> (первый игрок никогда не выиграет, если выход произойдёт мгновенно в точке <math>A</math>). Эти условия следуют из того, что <math>\lim\limits_{l\rightarrow\infty} \beta_l(B) = \beta(B)</math>. Это также будет доказано в этом разделе.
Сначала получим решение уравнения <math>\beta(x) = p\beta(x+1) + q\beta(x-1)</math>. Пусть игра несправедливая (<math>p\ne q</math>). В таком случае найдём корни уравнения, то есть <math>\beta(x)</math>. Одно частное решение видно сразу: <math>\beta(x) = \mathrm{const} = a</math>. Другое решение найдём, воспользовавшись тем, что <math>\beta(x)</math> — функция. Целесообразно употребить выражение с отношением <math>\frac{q}{p}</math>, учитывая, что <math>p+q=1</math>: <math>\left( \frac{q}{p} \right)^x = \frac{q^x(p+q)}{p^x} = \frac{q^x}{p^{x-1}} + \frac{q^{x+1}}{p^x} = p\frac{q^{x+1}}{p^{x+1}} + q\frac{q^{x-1}}{p^{x-1}} = p\left(\frac{q}{p}\right)^{x+1} + q\left(\frac{q}{p}\right)^{x-1}</math>. Отсюда правомерно предположить, что <math>\beta(x) = b\cdot \left(\frac{q}{p}\right)^x</math>. Добавление константы ничего не изменит благодаря тому, что <math>p+q=1</math>.
Теперь рассмотрим общее решение: <math>\beta(x) = a + b\left(\frac{q}{p}\right)^x</math>. Воспользуемся теми условиями, что <math>\beta(A) = a+b\left(\frac{q}{p}\right)^A=0</math> и <math>\beta(B) = a+b\left(\frac{q}{p}\right)^B=1</math>, и получим, что <math>\beta(x) = \frac{\beta(x)-0}{1-0} = \frac{\beta(x)-\beta(A)}{\beta(B)-\beta(A)} = \frac{a + b\left( \frac{q}{p}\right)^{x} - \left( a + b\left( \frac{q}{p}\right)^{A} \right)}{a + b\left( \frac{q}{p}\right)^{B} - \left( a + b\left( \frac{q}{p}\right)^{A} \right)} = \frac{\left( \frac{q}{p}\right)^{x}-\left( \frac{q}{p}\right)^{A}}{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{A}}.</math>
Подзадача о единственности решения
Докажем единственность решения данной задачи. Для этого покажем, что любое решение задачи <math>\beta(x) = p\beta(x+1) + q\beta(x-1)</math> с граничными условиями может быть представлено в виде <math>\frac{\left( \frac{q}{p}\right)^{x}-\left( \frac{q}{p}\right)^{A}}{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{A}}</math>.
Решение. Рассмотрим некоторое решение <math>\check \beta(x)</math> при условиях <math>\check\beta (A)=0</math>, <math>\check\beta(B)=1</math>. Тогда всегда можно подобрать такие константы <math>\check a</math> и <math>\check b</math>, что <math>\check a + \check b \left( \frac{q}{p}\right)^{A} = \check\beta(A)</math>, <math>\check a + \check b\left( \frac{q}{p}\right)^{A+1} = \check \beta(A+1)</math>. Тогда из уравнения поставленной задачи следует, что <math>\check\beta(A+2) = \check a + \check b \left( \frac{q}{p}\right)^{A+2}</math>. Тогда в общем случае <math>\check \beta(x) = \check a + \check b\left( \frac{q}{p}\right)^{x}</math>. Следовательно, решение <math>\frac{\left( \frac{q}{p}\right)^{x}-\left( \frac{q}{p}\right)^{A}}{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{A}}</math> является единственным. Точно такой же ход рассуждений может быть применён и к <math>\alpha(x)</math>. <math>\blacksquare</math>
Предельная сходимость
Рассмотрим вопрос о быстроте предельной сходимости <math>\alpha_n(x)</math> и <math>\beta_n(x)</math> к <math>\alpha(x)</math> и <math>\beta(x)</math>. Пусть блуждание начинается из начала координат (<math>x=0</math>). Для простоты обозначим <math>\alpha_n(0)=\alpha_n</math>, <math>\beta_n(0)=\beta_n</math>, <math>\gamma_n = 1-\alpha_n-\beta_n</math>. Иными словами, <math>\gamma_n</math> — это единица минус сумма вероятностей выхода частицы из коридора — вероятность того, что она останется блуждать в коридоре: <math>\gamma_n = \mathbb{P} \{ \omega\colon A<S_k<B; 0\leqslant k \leqslant n \}</math>. <math>\omega</math> представляет собой событие <math>\bigcap\limits_{0\leqslant k \leqslant n} \{ A<S_k<B \}</math>. Рассмотрим число <math>n=rm</math>, где <math>r,m\in \mathbb{Z}</math>, и цепочку случайных величин <math>\zeta_n\colon \zeta_1 = \sum\limits_{i=1}^m \xi_i,~\zeta_2 = \sum\limits_{i=m+1}^{2m} \xi_i,~\ldots{},~\zeta_r = \sum\limits_{i=m(r-1)}^{rm} \xi_i</math>. Если обозначить совокупное богатство за <math>C = |A| +B</math>, то тогда <math>\{A<S_k<B;1\leqslant k \leqslant rm \} \subseteq \bigl\{|\zeta_1|<C;\ldots{};|\zeta_r|<C\bigr\}</math>. Этому есть разумное объяснение: если частица выходит из нуля и не пересекает границ, то тогда совершенно определённо сумма <math>m</math> штук <math>x_i</math> меньше, чем совокупный запас.
Подзадача о независимости случайных величин <math>\zeta_i</math>
Докажем, что <math>\zeta_j</math> независимы и одинаково распределённые. Достаточно доказать, что они независимы, так как все они имеют биномиальное распределение.
Решение. Докажем, что <math>\mathbb{P}\bigl(\{ \zeta_1=m \} \cap \{ \zeta_2=m \} \bigr) = \mathbb{P} \bigl( \{\zeta_1=m\}\bigr) \cdot \mathbb{P}\bigl( \{\zeta_2=m\}\bigr).</math>
| <math>\mathbb{P}\bigl(\{ \zeta_1=m \} \cap \{ \zeta_2=m \} \bigr) = \mathbb{P} \left( \left\{ \sum\limits_{i=1}^{m} \xi_i = m \right\} \cap \left\{ \sum\limits_{i=m+1}^{2m} \xi_i = m \right\} \right) =</math> |
| <math>=\mathbb{P}\bigl( \{ \xi_{1;\ldots;m} = 1 \} \cap \{ \xi_{m+1;\ldots;2m} = 1\} \bigr) = \mathbb{P}^{2m}\bigl( \{\xi_i=1\}\bigr) = \mathbb{P} \bigl(\{\zeta_1=m\}\bigr) \cdot \mathbb{P} \bigl(\{\zeta_2=m\}\bigr)</math>. <math>\blacksquare</math> |
Вернёмся к рассмотрению сходимости. <math>\gamma_n \leqslant \mathbb{P} \Bigl( \bigl\{ |\zeta_1|;\ldots;|\zeta_r|<C\bigr\} \Bigr) = \prod\limits_{i=1}^r \mathbb{P} \Bigl( \bigl\{ |\zeta_i|<C \bigr\} \Bigr) = \biggl( \mathbb{P} \Bigl( \bigl\{ |\zeta_1|<C \bigr\} \Bigr) \biggr)^r</math>, что следует из только что доказанного. Рассмотрим дисперсию: <math>\mathrm{Var}(\zeta_1) = m\bigl(1-(p-q)^2\bigr)</math> (что вполне правомерно, так как <math>1-(p-q)^2 =1-\bigl((p+q)^2-4pq\bigr)</math>, а <math>\xi</math> — модифицированная бернуллиевская случайная величина), поэтому для достаточно больших <math>m</math> и <math>0<p<1</math> верно: <math>\mathbb{P}\Bigl( \bigl\{ |\zeta_1|<C\bigr\} \Bigr) \leqslant \varepsilon_1</math>, где <math>\varepsilon_1<1</math>, так как если <math>\mathbb{P}\Bigl( \bigl\{ |\zeta_1|\leqslant C \bigr\} \Bigr)=1</math>, то <math>\mathrm{Var}(\zeta_1)\leqslant C^2</math>. Если <math>p=0</math> или <math>p=1</math>, то для довольно больших <math>m</math> верно, что <math>\mathbb{P}\Bigl( \bigl\{ |\zeta_1|<C \bigr\} \Bigr)=0</math>, поэтому неравенство <math>\mathbb{P}\Bigl( \bigl\{ |\zeta_1|<C \bigr\} \Bigr) \leqslant \varepsilon_1</math> верно <math>\forall p\in[0;1]</math>. Из вышесказанного следует, что <math>\gamma_n \leqslant \varepsilon^n</math>, где <math>\varepsilon = \varepsilon_1^{\frac{1}{m}}<1</math>. Так как <math>\alpha+\beta = 1</math>, то <math>(\alpha-\alpha_n)-(\beta-\beta_n)=\gamma_n</math>; так как <math>\alpha\geqslant \alpha_n</math> и <math>\beta\geqslant \beta_n</math>, то <math>0\leqslant \alpha-\alpha_n \leqslant \gamma_n \leqslant \varepsilon^n</math>; <math>0\leqslant \beta-\beta_n \leqslant \gamma_n \leqslant \varepsilon^n</math> при <math>\varepsilon<1</math>. Аналогичные оценки справедливы и для разностей <math>\alpha(x)-\alpha_n(x)</math> и <math>\beta(x)-\beta_n(x)</math>, так как можно свести эти разности к разностям <math>\alpha-\alpha_n</math> и <math>\beta-\beta_n</math> при <math>A_1 = A-x</math>, <math>B_1=B-x</math>.
Вернёмся к рассмотрению <math>\alpha(x)</math>. По аналогии с решением <math>\frac{\left( \frac{q}{p}\right)^{x}-\left( \frac{q}{p}\right)^{A}}{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{A}}</math> уравнения <math>\beta(x) = p\beta(x+1) + q\beta(x-1)</math>, можно сказать, что у уравнения <math>\alpha(x) = p\alpha(x+1) + q\alpha(x-1)</math> при граничных условиях <math>\alpha(A)=1</math>, <math>\alpha(B)=0</math> существует единственное решение <math>\alpha(x) = \frac{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{x}}{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{A}},\qquad A\leqslant x \leqslant B.</math>
Нетрудно заметить, что <math>\alpha(x) + \beta(x) = \frac{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{x}}{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{A}} + \frac{\left( \frac{q}{p}\right)^{x}-\left( \frac{q}{p}\right)^{A}}{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{A}} = \frac{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{A}}{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{A}}=1</math> при любых <math>p\in [0;1]</math>. Если же игра является справедливой (вероятность выпадения аверса равна вероятности выпадения реверса), то решения будут выглядеть следующим образом: <math>\beta(x) = \frac{x-A}{B-A}</math>, <math>\alpha(x) = \frac{B-x}{B-A}</math>.
Ответ о вероятности разорения
Величины <math>\alpha(x)</math> и <math>\beta(x)</math> было бы можно назвать вероятностями разорения первого и второго игрока при начальных капиталах <math>x-A</math> и <math>x-B</math> при стремлении количества ходов к бесконечности и характеризации случайной величина <math>\xi_i=+1</math> как выигрыша первого игрока, а <math>\xi_i=-1</math> — проигрыша первого игрока. В дальнейшем будет показано, почему такую последовательность действительно можно построить.
Если <math>A=0</math>, то интуитивный смысл функции <math>\beta(x)</math> — это вероятность того, что частица, вышедшая из положения <math>x</math>, достигнет верхней стенки (<math>B</math>) ранее, чем нуля. Из формул <math>\beta (x)</math> видно, что <math>\beta(x) = \begin{cases} \frac{x}{B}, & p=q=0{,}5,\\ \frac{\left( \frac{q}{p}\right)^{x}-1}{\left( \frac{q}{p}\right)^{B}-1}, & p\ne q \end{cases}</math>.
Парадокс увеличения ставки при неблагоприятной игре
Что необходимо сделать первому игроку, если игра неблагоприятна для него?
Его вероятность проигрыша задана формулой <math>\lim\limits_{k\rightarrow\infty} \alpha_k = \alpha = \frac{\left( \frac{q}{p}\right)^{B}-1}{\left( \frac{q}{p}\right)^{B}-\left( \frac{q}{p}\right)^{A}}</math>. Теперь пусть первый игрок с капиталом <math>(-A)</math> примет решение удвоить ставку и играть на два рубля. Теперь <math>\mathbb{P}\bigl( \{\xi_i=2\}\bigr)=p</math>, <math>\mathbb{P}\bigl( \{\xi_i=-2\}\bigr)=q</math>. Тогда обозначим предельную вероятность разорения первого игрока так: <math>\alpha_2</math>. Тогда <math>\alpha_2 = \frac{\left( \frac{q}{p}\right)^{0{,}5B}-1}{\left( \frac{q}{p}\right)^{0{,}5B}-\left( \frac{q}{p}\right)^{0{,}5A}}</math>. Поэтому <math>\alpha = \frac{\left( \frac{q}{p}\right)^{0{,}5B\cdot2} - 1^2}{ \left( \frac{q}{p}\right)^{0{,}5B\cdot2} - \left( \frac{q}{p}\right)^{0{,}5A\cdot2} } = \frac{\left( \left( \frac{q}{p}\right)^{0{,}5B}-1\right)\cdot \left( \left( \frac{q}{p}\right)^{0{,}5B}+1\right)}{\left( \left( \frac{q}{p}\right)^{0{,}5B}-\left( \frac{q}{p}\right)^{0{,}5A}\right) \cdot \left( \left( \frac{q}{p}\right)^{0{,}5B}+\left( \frac{q}{p}\right)^{0{,}5A}\right)} = \alpha_2 \cdot \frac{\left( \left( \frac{q}{p}\right)^{0{,}5B}+1\right)}{\left( \left( \frac{q}{p}\right)^{0{,}5B}+\left( \frac{q}{p}\right)^{0{,}5A}\right)} > \alpha_2</math>, так как <math>\alpha_2</math> умножается на дробь, которая больше единицы при <math>q>p</math>.
Поэтому если вероятность выпадения столь желанного для первого игрока аверса меньше <math>0{,}5</math>, то ему выгодно увеличить ставку в <math>r>1</math> раз: это уменьшает вероятность его терминального разорения за счёт того, что вырастает вероятность выскочить из коридора в точке <math>B</math>. Это решение кажется парадоксальным, так как складывается впечатление, что при неблагоприятной ситуации надо снизить ставку и уменьшить проигрыш, но в действительности при бесконечном числе игр и низкой ставке проигрывающий игрок в конечном счёте обязательно проиграется в ноль, а игрок с высокой ставкой обладает большими шансами выпадения количества аверсов, достаточного для завершения игры в точке <math>B</math>.
Длительность случайного блуждания
Рассмотрим среднюю длительность блуждания нашей частицы. Введём математическое ожидание момента, когда игра прекращается: <math>\mathbb{E}(\tau^x_k)= m_k(x)</math> для <math>k\leqslant n</math>. Выведем рекуррентное соотношение для математического ожидания продолжительности игры:
| \{ \xi_1=1 \}\bigr) + q\mathbb{P}\bigl(\{ \tau_k^x = l \} \big| \{ \xi_1=-1 \}\bigr) \Bigr) =</math> |
| <math>=
\sum\limits_{1\leqslant l \leqslant k} l \Bigl( p\mathbb{P}\bigl( \{ \tau_{k-1}^{x+1} = l-1 \}\bigr) + q\mathbb{P}\bigl\{ \tau_{k-1}^{x-1} = l-1 \}\bigr) \Bigr) = \sum\limits_{0\leqslant l \leqslant k-1} (l+1) \Bigl( p\mathbb{P}\bigl( \{ \tau_{k-1}^{x+1} = l\}\bigr) + q\mathbb{P}\bigl(\{ \tau_{k-1}^{x-1} = l \}\bigr) \Bigr) =</math> |
| <math>= pm_{k-1}(x+1) + qm_{k-1}(x-1) + \sum\limits_{0\leqslant l \leqslant k-1} \Bigl( p\mathbb{P}\bigl( \{ \tau_{k-1}^{x+1} = l\}\bigr) + q\mathbb{P}\bigl(\{ \tau_{k-1}^{x-1} = l \}\bigr) \Bigr) = pm_{k-1}(x+1) + qm_{k-1}(x-1) + 1.</math> |
Для <math>x\in (A;B)</math> и <math>k\in[0;n]</math> мы получили рекуррентное соотношение для функции <math>m_k(x)</math>: <math>m_k(x) = pm_{k-1}(x+1) + qm_{k-1}(x-1) + 1</math> при <math>m_0(x)=0</math>. Введём граничные условия: если игра начинается в точке <math>A</math> или <math>B</math>, то тогда она тут же и завершится — её длительность будет равна 0: <math>m_k(A) = m_k(B)=0</math>. Из рекуррентного соотношения и граничных условий можно один за другим вычислить <math>m_i(x)</math>. Так как <math>m_{k+1}(x) \geqslant m_k(x)</math>, то существует предел <math>m(x) = \lim\limits_{n\rightarrow\infty} m_n(x)</math>, который удовлетворяет соотношению <math>m_k(x) = pm_{k-1}(x+1) + qm_{k-1}(x-1) + 1</math>: <math>m(x) = 1+pm(x+1) + qm(x-1)</math> при выполнении <math>m(A)=m(B)=0</math>. Данные переходы аналогичны тем, что мы рассмотрели при переходе к <math>n\rightarrow\infty</math> в уравнении вероятности проигрыша. Для того чтобы решить данное уравнение, надо ввести ещё одно условие: матожидание количества ходов должно быть конечным, то есть <math>m(x)<\infty</math>, <math>x\in(A;B)</math>.
Решим данное уравнение. В уравнении вероятности проигрыша (<math>p\ne q</math>) уже были получены частные решения <math>a</math> и <math>b\left( \frac{q}{p}\right)^{x}</math>. Здесь же появляется ещё один претендент на роль частного решения: <math>\frac{x}{q-p} =\frac{q-p+(p+q)x + p-q}{q-p} = \frac{q-p}{q-p} + \frac{p(x+1)}{q-p} + \frac{q(x-1)}{q-p} = 1 + p\frac{x+1}{q-p} + q\frac{x-1}{q-p}</math>, поэтому <math>m(x) = \frac{x}{q-p} + a + b\left( \frac{q}{p}\right)^{x}</math>. С учётом граничного условия <math>m(A)=m(B)=0</math> находим при помощи ранее полученных соотношений <math>m(x)</math>: <math>m(x) = \frac{1}{p-q}\bigl( B\beta(x) + A\alpha(x) - x\bigr)</math>. В случае идеальной монетки получаем следующее выражение: <math>m(x) = a+bx-x^2</math>. Применение граничного условия даёт: <math>m(x)= (B-x)(x-A)</math>. Из этого следует, что в случае равных стартовых капиталов <math>m(0)=B^2</math>. Например, если у каждого игрока есть по 5 рублей, а ставка — 1 рубль, то в среднем разоряться игроки будут через 25 ходов.
При рассмотрении вышеуказанных формул подразумевалась конечностью математического ожидания числа ходов: <math>m(x)<\infty</math>. Теперь будет предложено доказательство этого факта.
Задача о конечности ожидаемого числа ходов
Доказать, что <math>m(x)<\infty\quad \forall A,B</math>.
Решение. Достаточно доказать это для случая <math>x=0</math> (так как ранее было уже продемонстрировано, что случаи <math>x\ne 0</math> могут быть сведены к <math>x=0</math> вариацией <math>A</math> и <math>B</math>) и <math>p=q</math>, а затем рассмотреть случай <math>p\ne q</math>. Итак, рассмотрим последовательность <math>S_{0;1;\ldots;n}</math> и введём случайную величину <math>S_{\tau_n} = S_{\tau_n}(\omega)</math>, где <math>\tau_n=\tau_n^0</math> — момент остановки. Далее, пусть <math>S_{\tau_n} (\omega) = \sum\limits_{k=0}^n S_k(\omega) \mathbf{1}_{\{ {\tau_n=k} \}}(\omega)</math>. Интерпретация такова: <math>S_{\tau_n}</math> — это значение случайного блуждания в момент <math>\tau_n</math>. Если <math>\tau_n<n</math>, то <math>S_{\tau_n}\in \{A;B\}</math>; если <math>\tau_n=n</math>, то <math>A\leqslant S_{\tau_n} \leqslant B</math>. Вспомним, что <math>p=q=0{,}5</math>, и докажем, что <math>\mathbb{E}(S_{\tau_n})=0</math>, <math>\mathbb{E}(S_{\tau_n}^2) = \mathbb{E}(\tau_n)</math>.
Для доказательства первого равенства напишем: <math>\mathbb{E}(S_{\tau_n}) = \sum\limits_{k=0}^n \mathbb{E} \bigl(S_k\mathbf{1}_{\{ {\tau_n=k} \}}(\omega)\bigr) = \sum\limits_{k=0}^n \mathbb{E} \bigl( S_n\mathbf{1}_{\{ {\tau_n=k} \}}(\omega) \bigr) + \sum\limits_{k=0}^n \bigl( (S_k-S_n)\mathbf{1}_{\{ {\tau_n=k} \}}(\omega) \bigr) = \mathbb{E}(S_n) + \sum\limits_{k=0}^n \bigl( (S_k-S_n)\mathbf{1}_{\{ {\tau_n=k} \}}(\omega) \bigr)</math>. Совершенно очевидно, что <math>\mathbb{E}(S_n)=0</math>, так как <math>S_n = \xi_1+\ldots+\xi_n</math>, <math>\xi_i=\pm 1</math> при <math>p=q</math>. Осталось доказать, что <math>\sum\limits_{k=0}^n \bigl( (S_k-S_n)\mathbf{1}_{\{ {\tau_n=k} \}}(\omega) \bigr) = 0</math>. Для <math>0\leqslant k < n</math> справедливо, что <math>\{ \tau_n>k \} = \{ A<S_1<B;\ldots;A<S_k<B\}</math>. Последнее событие может быть представлено в виде <math>\bigl\{\omega\colon (\xi_1;\ldots;\xi_n)\in J \bigr\}</math>, где <math>J</math> — некоторое подмножество множества <math>\{ -1;+1 \}^k</math>. Это множество определяется только <math>\xi_i</math> при <math>i=\overline{1;k}</math>. Для бо́льших <math>i</math> значения <math>\xi_{k+1};\ldots;\xi_n</math> не влияют на <math>J</math>. Множество вида <math>\{ \tau_n=k \} = \{ \tau_n>k-1 \} \backslash \{ \tau_n>k \}</math> также может быть представлено в виде <math>\bigl\{\omega\colon (\xi_1;\ldots;\xi_n)\in J \bigr\}</math>. Благодаря независимости <math>\xi_i</math> (доказано в подзадаче 2) вытекает, что <math>\forall 0\leqslant k < n</math> случайные величины <math>S_n-S_k</math> и <math>\mathbf{1}_{\{ \tau_n=k \}}</math> независимы. Отсюда <math>\mathbb{E} \bigl( S_k\cdot\mathbf{1}_{\{ {\tau_n=k} \}}(\omega)\bigr) = \mathbb{E}(S_k)\cdot \mathbb{E}\bigl(\mathbf{1}_{\{ {\tau_n=k} \}}(\omega)\bigr)=0</math> в силу того, что первый множитель нулевой.
| <math> \mathbb{E}(S_{\tau_n}^2) = \sum\limits_{k=0}^n \mathbb{E} ( S^2_k \mathbf{1}_{\{ {\tau_n=k} \}}) = </math> |
| <math> = \sum\limits_{k=0}^n \mathbb{E} \Bigl( \bigl(S_n +(S_k - S_n)^2\bigr) \mathbf{1}_{\{{\tau_n=k}\}}\Bigr) =
\sum\limits_{k=0}^n \Bigl( \mathbb{E}(S^2)\mathbf{1}_{\{{\tau_n=k}\}} + 2\mathbb{E} \bigl( S_n (S_k - S_n)\bigr) \mathbf{1}_{\{{\tau_n=k}\}} + \mathbb{E} \bigl( (S_n-S_k)^2 \bigr)\mathbf{1}_{\{{\tau_n=k}\}} \Bigr) = </math> |
| <math>=\mathbb{E}(S^2) - \sum\limits_{k=0}^n \mathbb{E} \bigl( (S_n-S_k)^2 \bigr)\mathbf{1}_{\{{\tau_n=k}\}} = n - \sum\limits_{k=0}^n \mathbb{E} (n-k)\mathbb{P}\bigl( \{\tau_n=k\}\bigr) = \sum\limits_{k=0}^n k\mathbb{P}\bigl(\{\tau_n=k\}\bigr) = \mathbb{E}(\tau_n).</math> |
Установлено, что для идеальной монетки <math>\mathbb{E}(S_{\tau_n})=0</math>, <math>\mathbb{E}(S_{\tau_n}^2) = \mathbb{E}(\tau_n)</math>. В случае же <math>p\ne q</math> имеют место соотношения <math>\mathbb{E}(S_{\tau_n}) = (p-q)\mathbb{E}(\tau_n)</math> (поскольку <math>\mathbb{E}(\xi_1) = p-q</math>) и <math>\mathbb{E}\Bigl( \bigl(S_{\tau_n} - \tau_n \mathbb{E}(\xi_1)\bigr)^2 \Bigr) = \mathrm{Var}(\xi_1) \cdot \mathbb{E}(\tau_n)</math>, поскольку <math>\mathrm{Var}(\xi_1) = 1-(p-q)^2</math>. Теперь покажем, что <math>\lim\limits_{n\rightarrow\infty} m_n(0) = m(0)<\infty</math>. В случае справедливой игры в силу соотношения <math>\mathbb{E}(S_{\tau_n}^2) = \mathbb{E}(\tau_n)</math> верно, что <math>\mathbb{E}(\tau_n)\leqslant \max\{ A^2;B^2\}</math>. Тогда же <math>\mathbb{E} (\tau_n) = \mathbb{E}(S^2_{\tau_n}) = A^2 \alpha_n + B^2 \beta_n + \mathbb{E} (S^2_n \mathbf{1}_{\{{A<S_n<B}\}}) \mathbf{1}_{\{{\tau_n=n}\}}</math>, поэтому <math>A^2 \alpha_n + B^2 \beta_n \leqslant \mathbb{E}(\tau_n) \leqslant A^2 \alpha_n + B^2 \beta_n + \max\{ A^2;B^2 \}\cdot \gamma_n</math>. Из неравенства <math>\gamma_n<\varepsilon^n</math> следует, что математическое ожидание <math>\mathbb{E}(\tau_n)</math> сходится при <math>n\rightarrow\infty</math> к предельному значению <math>m(0) = A^2\alpha + B^2 \beta = A^2 \cdot \frac{B}{B-A} - B^2\cdot \frac{A}{B-A} = |AB|</math>. В случае несправедливой игры <math>\mathbb{E}(\tau_n)\leqslant \frac{\max\{ |A|;B \}}{|p-q|}</math>. Так как за <math>\tau_n</math> обозначался момент первого вылета частицы за пределы коридора, то математическое ожидание его меньше определённых чисел, следовательно, меньше бесконечности. При таком условии <math>\mathbb{E}(\tau_n)\rightarrow m(0) = \frac{\alpha A + \beta B}{p-q}</math>. <math>\blacksquare</math>
Компьютерное моделирование (метод Монте-Карло)
Для моделирования игры воспользуемся программой MATLAB.
Для начала сгенерируем последовательность <math>\xi_i</math>, а затем при некотором первоначальном богатстве <math>x</math> создадим цепочку <math>S_k</math>:
Последовательность <math>\xi</math> (getXI)
n = 100; % The length of \xi_i series
U = rand(n,1); % Generate 100 random uniform [0;1] values
XI = zeros(n,1); % Reserve memory for 100 modified Bernoulli
q = 0.55; % Reverse probability
p = 1 - q; % Averse probability
% The following cycle creates a Bernoulli distribution based on uniform [0;1]
for i = 1:n % This cycle divides the [0;1] array into 2 parts: lengths q and p, q+p=1
if (U(i,1) < q)
XI(i,1) = -1; % If a uniform random value falls into q then \xi=-1
else XI(i,1) = 1; % If a uniform random value falls into p then \xi=+1
end
end
x = 10; % Initial 1st player's budget offset
S = zeros(n,1); % Reserve memory for 100 S_1...S_100
for i = 1:n % Make S_k series according to rule S_{k+1} = S_k + \xi_{k+1}
S(i,1) = x + sum(XI(1:i, 1)); % considering the initial welfare offset x
endЗатем введём функцию getS(n, q, x), которая бы не просто, как листинг выше, генерировала ряд <math>S_k</math> сразу и мгновенно, а позволяла бы обобщённо на основе введённых значений <math>n</math>, <math>q</math> и <math>x</math> построить ряд, не усложняя вычислений. Это бы упростило рабочую область.
Генерация ряда (getS function)
function [S] = getS(n, q, x) % This function depends on n, q and x --- 3 variables
U = rand(n,1);
XI = zeros(n,1);
for i = 2:n % Uniform->Bernoulli distribution transformation
if (U(i,1) < q)
XI(i,1) = -1;
else XI(i,1) = 1;
end
end
S = zeros(n,1); % Reserve memory for n S_1...S_n
for i = 2:n % Calculate the S_1...S_n series
S(i,1) = sum(XI(1:i, 1)); % Sums the \xi's
end
S = x + S; % Adds initial welfare to each S_k of the whole matrixВозникает разумный вопрос: зачем считать <math>\xi</math>, начиная только со второй величины (for i = 2:n)? Дело в том, что это делается исключительно в целях наглядной визуализации. При построении графика в следующем коде будут строиться траектории <math>S_k</math>, и если бы было написано for i = 1:n, то тогда уже с самого первого значения некоторые траектории бы выходили из <math>x-1</math>, некоторые — из <math>x+1</math>. Так как в данной программе из соображений оптимальности лучше не задействовать нулевое значение (из него частица выходит, но не рисуется, так как прибавление <math>\xi_1</math> происходит сразу), то просто-напросто сдвинем нумерацию на оси абсцисс на единицу вправо. Теперь проведём серию тестов и наглядно рассмотрим возможные траектории при некоторых вероятностях, длинах игры и количестве игр.
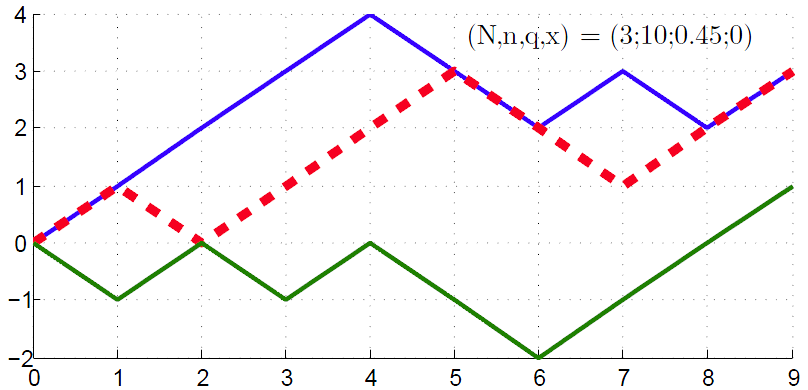
Визуализация (graphS)
N = 3; % Number of games played
n = 10; % Number of tosses
q = 0.45; % Chance 1st player loses 1 rouble
x = 0; % Initial welfare offset
matrS = zeros(N, n); % Reserve memory for N rows n cols matrix
for i = 1:N % This loop fills the S matrix with S_k, yielding N trajectories
matrS(i,:) = getS(n, q, x)';
plot(matrS(i,:)); % Gives an image
hold on; % Holds the axes for next trajectory overlay
end
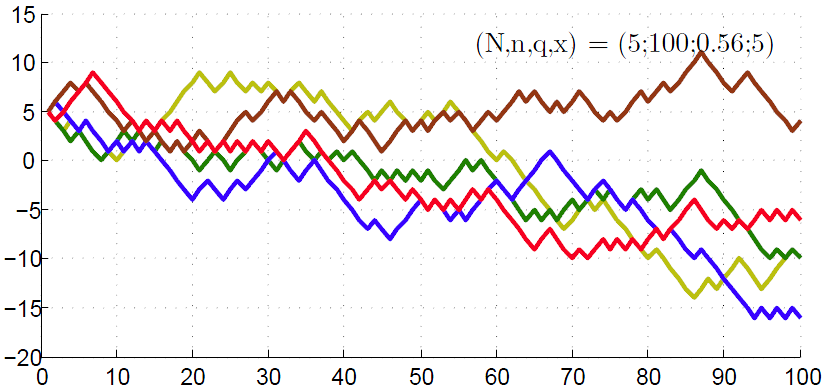
hold off; % Clears axes for a new plotТеперь подойдём к самой главной составляющей программной части — алгоритму, который позволил бы вычислять среднюю длину игры при заданных параметрах <math>(A;B;n;q)</math>. Если теория верна, то нижеследующий эксперимент её лишь подтвердит. Также допишем в программу строчку, которая будет вычислять вероятность разорения первого игрока (<math>\beta(x)</math>) при заданных начальных капиталах и сопоставлять её с теоретической.
Полная модель игры (Monte_Carlo)
N = 3000; % Number of games played
n = 3000; % Number of tosses
q = 0.5; % Chance 1st player loses 1 rouble
p = 1-q; % Chance 1st player wins 1 rouble
A = -10; % 1st player budget
B = 10; % 2nd player budget
x = 0; % Budget offset towards 1st player
Bs = 0; % amount of cases particle hits B (it will change soon)
As = 0; % amount of cases particle hits A (it will change soon)
matrS = zeros(N, n); % Reserve memory for N rows n cols matrix
TAU1 = n * ones(N, n); % Fill another N rows n cols matrix with n's
for i = 1:N % This loop makes up N trajectories of S_k relying on input q, x, n
matrS(i,:) = getS(n, q, x)';
for j = 1:n
if (matrS(i,j) == A)||(matrS(i,j) == B) % If a particle exceeds A or B, then
TAU1(i,j) = j; % put the number of step into the table
end
end
plot(matrS(i,:)); % Displays a figure
grid on;
hold on; % Simultaneous plots within same axes
end
hold off; % Clears axes for a new plot
TAU = (min(TAU1'))'; % TAU = earliest step of [A;B] corridor overrun
% As [min] affects columns and gives row then we transpose TAU1,
% minimize it by rows and make it a column again
for i = 1:N % Our S_n series are ready; they nest in matrS
for j=1:TAU(i) % Scan only till we encounter the escape step!
if (matrS(i,j) == A); % If a particle escaped through A (1st player busted)
As = As+1; % then add +1 to 1st player's failures
elseif (matrS(i,j) == B) % Otherwise if its first threshold was B
Bs = Bs+1; % then add +1 to 1st player's wins
end % If n is not large enough, then
end % As + Bs may not make up N
end
ALPHA = As/(As+Bs) % Match alphas with their theoretical values
if (q == p)
THEORALPHA = (B-x)/(B-A)
else THEORALPHA = ((q/p)^B - (q/p)^x)/((q/p)^B - (q/p)^A)
end
BETA = 1-ALPHA % Same for betas
if (q == p)
THEORBETA = (x-A)/(B-A)
else THEORBETA = 1-THEORALPHA
end
meanTAU = mean(TAU) % Law of large numbers for great N's
if (q == p)
THEORTAU = (B-x)*(x-A)
else THEORTAU = 1/(p-q)*(B*THEORBETA+A*THEORALPHA-x)
endОтметим, что при небольших <math>n</math> не все частицы вылетают из коридора, поэтому здесь надо подчеркнуть, что теория говорит: «при достаточно больших <math>n</math> вероятность <math>\beta_n(x)</math> близка к <math>\beta(x)</math>».
Тестирование
Нижеследующие данные рассчитаны для <math>n=3000</math>, <math>N = 3000</math>.
| № теста | <math>q</math> | <math>A</math> | <math>B</math> | <math>x</math> | ALPHA | <math>\alpha(x)</math> | BETA | <math>\beta(x)</math> | meanTAU | <math>m(x)</math> |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | <math>0{,}49</math> | <math>-6</math> | <math>5</math> | <math>0</math> | <math>0{,}4020</math> | <math>0{,}4006</math> | <math>0{,}5980</math> | <math>0{,}5994</math> | <math>30{,}9307</math> | <math>29{,}6856</math> |
| 2 | <math>0{,}6</math> | <math>-60</math> | <math>6</math> | <math>-3</math> | <math>0{,}9733</math> | <math>0{,}9740</math> | <math>0{,}0267</math> | <math>0{,}0260</math> | <math>278{,}2200</math> | <math>276{,}4159</math> |
| 3 | <math>0{,}6</math> | <math>-20</math> | <math>2</math> | <math>-1</math> | <math>0{,}7040</math> | <math>0{,}7038</math> | <math>0{,}2960</math> | <math>0{,}2962</math> | <math>62{,}2680</math> | <math>62{,}4178</math> |
| 4 | <math>0{,}54</math> | <math>-10</math> | <math>50</math> | <math>10</math> | <math>0{,}9990</math> | <math>0{,}9984</math> | <math>0{,}0010</math> | <math>0{,}0016</math> | <math>251{,}3587</math> | <math>248{,}8205</math> |
| 5 | <math>0{,}5</math> | <math>-10</math> | <math>20</math> | <math>0</math> | <math>0{,}6580</math> | <math>0{,}6667</math> | <math>0{,}3420</math> | <math>0{,}3333</math> | <math>202{,}3007</math> | <math>200{,}0000</math> |
| 6 | <math>0{,}35</math> | <math>-3</math> | <math>90</math> | <math>0</math> | <math>0{,}1457</math> | <math>0{,}1561</math> | <math>0{,}8543</math> | <math>0{,}8439</math> | <math>256{,}4557</math> | <math>251{,}6022</math> |
В экспериментах 2 и 3 продемонстрировано свойство: если игра проигрышная для первого игрока, то увеличение ставки в модели эквивалентно сокращению <math>A</math>, <math>B</math> и <math>x</math> в одно и то же число раз относительно нуля. Ставка увеличилась втрое — вероятность выскочить из коридора со значением <math>B</math> выросла в 11 раз!
См. также
- Случайное блуждание
- Случайный процесс
- Формула полной вероятности
- Распределение Бернулли
- Метод Монте-Карло
Напишите отзыв о статье "Задача о разорении игрока"
Примечания
- ↑ Ширяев А. Н. Вероятность—1, Вероятность—2 // Москва, МЦНМО. — 2007.
Отрывок, характеризующий Задача о разорении игрока
Через неделю Пьер, простившись с новыми друзьями масонами и оставив им большие суммы на милостыни, уехал в свои именья. Его новые братья дали ему письма в Киев и Одессу, к тамошним масонам, и обещали писать ему и руководить его в его новой деятельности.Дело Пьера с Долоховым было замято, и, несмотря на тогдашнюю строгость государя в отношении дуэлей, ни оба противника, ни их секунданты не пострадали. Но история дуэли, подтвержденная разрывом Пьера с женой, разгласилась в обществе. Пьер, на которого смотрели снисходительно, покровительственно, когда он был незаконным сыном, которого ласкали и прославляли, когда он был лучшим женихом Российской империи, после своей женитьбы, когда невестам и матерям нечего было ожидать от него, сильно потерял во мнении общества, тем более, что он не умел и не желал заискивать общественного благоволения. Теперь его одного обвиняли в происшедшем, говорили, что он бестолковый ревнивец, подверженный таким же припадкам кровожадного бешенства, как и его отец. И когда, после отъезда Пьера, Элен вернулась в Петербург, она была не только радушно, но с оттенком почтительности, относившейся к ее несчастию, принята всеми своими знакомыми. Когда разговор заходил о ее муже, Элен принимала достойное выражение, которое она – хотя и не понимая его значения – по свойственному ей такту, усвоила себе. Выражение это говорило, что она решилась, не жалуясь, переносить свое несчастие, и что ее муж есть крест, посланный ей от Бога. Князь Василий откровеннее высказывал свое мнение. Он пожимал плечами, когда разговор заходил о Пьере, и, указывая на лоб, говорил:
– Un cerveau fele – je le disais toujours. [Полусумасшедший – я всегда это говорил.]
– Я вперед сказала, – говорила Анна Павловна о Пьере, – я тогда же сейчас сказала, и прежде всех (она настаивала на своем первенстве), что это безумный молодой человек, испорченный развратными идеями века. Я тогда еще сказала это, когда все восхищались им и он только приехал из за границы, и помните, у меня как то вечером представлял из себя какого то Марата. Чем же кончилось? Я тогда еще не желала этой свадьбы и предсказала всё, что случится.
Анна Павловна по прежнему давала у себя в свободные дни такие вечера, как и прежде, и такие, какие она одна имела дар устроивать, вечера, на которых собиралась, во первых, la creme de la veritable bonne societe, la fine fleur de l'essence intellectuelle de la societe de Petersbourg, [сливки настоящего хорошего общества, цвет интеллектуальной эссенции петербургского общества,] как говорила сама Анна Павловна. Кроме этого утонченного выбора общества, вечера Анны Павловны отличались еще тем, что всякий раз на своем вечере Анна Павловна подавала своему обществу какое нибудь новое, интересное лицо, и что нигде, как на этих вечерах, не высказывался так очевидно и твердо градус политического термометра, на котором стояло настроение придворного легитимистского петербургского общества.
В конце 1806 года, когда получены были уже все печальные подробности об уничтожении Наполеоном прусской армии под Иеной и Ауерштетом и о сдаче большей части прусских крепостей, когда войска наши уж вступили в Пруссию, и началась наша вторая война с Наполеоном, Анна Павловна собрала у себя вечер. La creme de la veritable bonne societe [Сливки настоящего хорошего общества] состояла из обворожительной и несчастной, покинутой мужем, Элен, из MorteMariet'a, обворожительного князя Ипполита, только что приехавшего из Вены, двух дипломатов, тетушки, одного молодого человека, пользовавшегося в гостиной наименованием просто d'un homme de beaucoup de merite, [весьма достойный человек,] одной вновь пожалованной фрейлины с матерью и некоторых других менее заметных особ.
Лицо, которым как новинкой угащивала в этот вечер Анна Павловна своих гостей, был Борис Друбецкой, только что приехавший курьером из прусской армии и находившийся адъютантом у очень важного лица.
Градус политического термометра, указанный на этом вечере обществу, был следующий: сколько бы все европейские государи и полководцы ни старались потворствовать Бонапартию, для того чтобы сделать мне и вообще нам эти неприятности и огорчения, мнение наше на счет Бонапартия не может измениться. Мы не перестанем высказывать свой непритворный на этот счет образ мыслей, и можем сказать только прусскому королю и другим: тем хуже для вас. Tu l'as voulu, George Dandin, [Ты этого хотел, Жорж Дандэн,] вот всё, что мы можем сказать. Вот что указывал политический термометр на вечере Анны Павловны. Когда Борис, который должен был быть поднесен гостям, вошел в гостиную, уже почти всё общество было в сборе, и разговор, руководимый Анной Павловной, шел о наших дипломатических сношениях с Австрией и о надежде на союз с нею.
Борис в щегольском, адъютантском мундире, возмужавший, свежий и румяный, свободно вошел в гостиную и был отведен, как следовало, для приветствия к тетушке и снова присоединен к общему кружку.
Анна Павловна дала поцеловать ему свою сухую руку, познакомила его с некоторыми незнакомыми ему лицами и каждого шопотом определила ему.
– Le Prince Hyppolite Kouraguine – charmant jeune homme. M r Kroug charge d'affaires de Kopenhague – un esprit profond, и просто: М r Shittoff un homme de beaucoup de merite [Князь Ипполит Курагин, милый молодой человек. Г. Круг, Копенгагенский поверенный в делах, глубокий ум. Г. Шитов, весьма достойный человек] про того, который носил это наименование.
Борис за это время своей службы, благодаря заботам Анны Михайловны, собственным вкусам и свойствам своего сдержанного характера, успел поставить себя в самое выгодное положение по службе. Он находился адъютантом при весьма важном лице, имел весьма важное поручение в Пруссию и только что возвратился оттуда курьером. Он вполне усвоил себе ту понравившуюся ему в Ольмюце неписанную субординацию, по которой прапорщик мог стоять без сравнения выше генерала, и по которой, для успеха на службе, были нужны не усилия на службе, не труды, не храбрость, не постоянство, а нужно было только уменье обращаться с теми, которые вознаграждают за службу, – и он часто сам удивлялся своим быстрым успехам и тому, как другие могли не понимать этого. Вследствие этого открытия его, весь образ жизни его, все отношения с прежними знакомыми, все его планы на будущее – совершенно изменились. Он был не богат, но последние свои деньги он употреблял на то, чтобы быть одетым лучше других; он скорее лишил бы себя многих удовольствий, чем позволил бы себе ехать в дурном экипаже или показаться в старом мундире на улицах Петербурга. Сближался он и искал знакомств только с людьми, которые были выше его, и потому могли быть ему полезны. Он любил Петербург и презирал Москву. Воспоминание о доме Ростовых и о его детской любви к Наташе – было ему неприятно, и он с самого отъезда в армию ни разу не был у Ростовых. В гостиной Анны Павловны, в которой присутствовать он считал за важное повышение по службе, он теперь тотчас же понял свою роль и предоставил Анне Павловне воспользоваться тем интересом, который в нем заключался, внимательно наблюдая каждое лицо и оценивая выгоды и возможности сближения с каждым из них. Он сел на указанное ему место возле красивой Элен, и вслушивался в общий разговор.
– Vienne trouve les bases du traite propose tellement hors d'atteinte, qu'on ne saurait y parvenir meme par une continuite de succes les plus brillants, et elle met en doute les moyens qui pourraient nous les procurer. C'est la phrase authentique du cabinet de Vienne, – говорил датский charge d'affaires. [Вена находит основания предлагаемого договора до того невозможными, что достигнуть их нельзя даже рядом самых блестящих успехов: и она сомневается в средствах, которые могут их нам доставить. Это подлинная фраза венского кабинета, – сказал датский поверенный в делах.]
– C'est le doute qui est flatteur! – сказал l'homme a l'esprit profond, с тонкой улыбкой. [Сомнение лестно! – сказал глубокий ум,]
– Il faut distinguer entre le cabinet de Vienne et l'Empereur d'Autriche, – сказал МorteMariet. – L'Empereur d'Autriche n'a jamais pu penser a une chose pareille, ce n'est que le cabinet qui le dit. [Необходимо различать венский кабинет и австрийского императора. Австрийский император никогда не мог этого думать, это говорит только кабинет.]
– Eh, mon cher vicomte, – вмешалась Анна Павловна, – l'Urope (она почему то выговаривала l'Urope, как особенную тонкость французского языка, которую она могла себе позволить, говоря с французом) l'Urope ne sera jamais notre alliee sincere. [Ах, мой милый виконт, Европа никогда не будет нашей искренней союзницей.]
Вслед за этим Анна Павловна навела разговор на мужество и твердость прусского короля с тем, чтобы ввести в дело Бориса.
Борис внимательно слушал того, кто говорит, ожидая своего череда, но вместе с тем успевал несколько раз оглядываться на свою соседку, красавицу Элен, которая с улыбкой несколько раз встретилась глазами с красивым молодым адъютантом.
Весьма естественно, говоря о положении Пруссии, Анна Павловна попросила Бориса рассказать свое путешествие в Глогау и положение, в котором он нашел прусское войско. Борис, не торопясь, чистым и правильным французским языком, рассказал весьма много интересных подробностей о войсках, о дворе, во всё время своего рассказа старательно избегая заявления своего мнения насчет тех фактов, которые он передавал. На несколько времени Борис завладел общим вниманием, и Анна Павловна чувствовала, что ее угощенье новинкой было принято с удовольствием всеми гостями. Более всех внимания к рассказу Бориса выказала Элен. Она несколько раз спрашивала его о некоторых подробностях его поездки и, казалось, весьма была заинтересована положением прусской армии. Как только он кончил, она с своей обычной улыбкой обратилась к нему:
– Il faut absolument que vous veniez me voir, [Необходимо нужно, чтоб вы приехали повидаться со мною,] – сказала она ему таким тоном, как будто по некоторым соображениям, которые он не мог знать, это было совершенно необходимо.
– Mariedi entre les 8 et 9 heures. Vous me ferez grand plaisir. [Во вторник, между 8 и 9 часами. Вы мне сделаете большое удовольствие.] – Борис обещал исполнить ее желание и хотел вступить с ней в разговор, когда Анна Павловна отозвала его под предлогом тетушки, которая желала его cлышать.
– Вы ведь знаете ее мужа? – сказала Анна Павловна, закрыв глаза и грустным жестом указывая на Элен. – Ах, это такая несчастная и прелестная женщина! Не говорите при ней о нем, пожалуйста не говорите. Ей слишком тяжело!
Когда Борис и Анна Павловна вернулись к общему кружку, разговором в нем завладел князь Ипполит.
Он, выдвинувшись вперед на кресле, сказал: Le Roi de Prusse! [Прусский король!] и сказав это, засмеялся. Все обратились к нему: Le Roi de Prusse? – спросил Ипполит, опять засмеялся и опять спокойно и серьезно уселся в глубине своего кресла. Анна Павловна подождала его немного, но так как Ипполит решительно, казалось, не хотел больше говорить, она начала речь о том, как безбожный Бонапарт похитил в Потсдаме шпагу Фридриха Великого.
– C'est l'epee de Frederic le Grand, que je… [Это шпага Фридриха Великого, которую я…] – начала было она, но Ипполит перебил ее словами:
– Le Roi de Prusse… – и опять, как только к нему обратились, извинился и замолчал. Анна Павловна поморщилась. MorteMariet, приятель Ипполита, решительно обратился к нему:
– Voyons a qui en avez vous avec votre Roi de Prusse? [Ну так что ж о прусском короле?]
Ипполит засмеялся, как будто ему стыдно было своего смеха.
– Non, ce n'est rien, je voulais dire seulement… [Нет, ничего, я только хотел сказать…] (Он намерен был повторить шутку, которую он слышал в Вене, и которую он целый вечер собирался поместить.) Je voulais dire seulement, que nous avons tort de faire la guerre рour le roi de Prusse. [Я только хотел сказать, что мы напрасно воюем pour le roi de Prusse . (Непереводимая игра слов, имеющая значение: «по пустякам».)]
Борис осторожно улыбнулся так, что его улыбка могла быть отнесена к насмешке или к одобрению шутки, смотря по тому, как она будет принята. Все засмеялись.
– Il est tres mauvais, votre jeu de mot, tres spirituel, mais injuste, – грозя сморщенным пальчиком, сказала Анна Павловна. – Nous ne faisons pas la guerre pour le Roi de Prusse, mais pour les bons principes. Ah, le mechant, ce prince Hippolytel [Ваша игра слов не хороша, очень умна, но несправедлива; мы не воюем pour le roi de Prusse (т. e. по пустякам), а за добрые начала. Ах, какой он злой, этот князь Ипполит!] – сказала она.
Разговор не утихал целый вечер, обращаясь преимущественно около политических новостей. В конце вечера он особенно оживился, когда дело зашло о наградах, пожалованных государем.
– Ведь получил же в прошлом году NN табакерку с портретом, – говорил l'homme a l'esprit profond, [человек глубокого ума,] – почему же SS не может получить той же награды?
– Je vous demande pardon, une tabatiere avec le portrait de l'Empereur est une recompense, mais point une distinction, – сказал дипломат, un cadeau plutot. [Извините, табакерка с портретом Императора есть награда, а не отличие; скорее подарок.]
– Il y eu plutot des antecedents, je vous citerai Schwarzenberg. [Были примеры – Шварценберг.]
– C'est impossible, [Это невозможно,] – возразил другой.
– Пари. Le grand cordon, c'est different… [Лента – это другое дело…]
Когда все поднялись, чтоб уезжать, Элен, очень мало говорившая весь вечер, опять обратилась к Борису с просьбой и ласковым, значительным приказанием, чтобы он был у нее во вторник.
– Мне это очень нужно, – сказала она с улыбкой, оглядываясь на Анну Павловну, и Анна Павловна той грустной улыбкой, которая сопровождала ее слова при речи о своей высокой покровительнице, подтвердила желание Элен. Казалось, что в этот вечер из каких то слов, сказанных Борисом о прусском войске, Элен вдруг открыла необходимость видеть его. Она как будто обещала ему, что, когда он приедет во вторник, она объяснит ему эту необходимость.
Приехав во вторник вечером в великолепный салон Элен, Борис не получил ясного объяснения, для чего было ему необходимо приехать. Были другие гости, графиня мало говорила с ним, и только прощаясь, когда он целовал ее руку, она с странным отсутствием улыбки, неожиданно, шопотом, сказала ему: Venez demain diner… le soir. Il faut que vous veniez… Venez. [Приезжайте завтра обедать… вечером. Надо, чтоб вы приехали… Приезжайте.]
В этот свой приезд в Петербург Борис сделался близким человеком в доме графини Безуховой.
Война разгоралась, и театр ее приближался к русским границам. Всюду слышались проклятия врагу рода человеческого Бонапартию; в деревнях собирались ратники и рекруты, и с театра войны приходили разноречивые известия, как всегда ложные и потому различно перетолковываемые.
Жизнь старого князя Болконского, князя Андрея и княжны Марьи во многом изменилась с 1805 года.
В 1806 году старый князь был определен одним из восьми главнокомандующих по ополчению, назначенных тогда по всей России. Старый князь, несмотря на свою старческую слабость, особенно сделавшуюся заметной в тот период времени, когда он считал своего сына убитым, не счел себя вправе отказаться от должности, в которую был определен самим государем, и эта вновь открывшаяся ему деятельность возбудила и укрепила его. Он постоянно бывал в разъездах по трем вверенным ему губерниям; был до педантизма исполнителен в своих обязанностях, строг до жестокости с своими подчиненными, и сам доходил до малейших подробностей дела. Княжна Марья перестала уже брать у своего отца математические уроки, и только по утрам, сопутствуемая кормилицей, с маленьким князем Николаем (как звал его дед) входила в кабинет отца, когда он был дома. Грудной князь Николай жил с кормилицей и няней Савишной на половине покойной княгини, и княжна Марья большую часть дня проводила в детской, заменяя, как умела, мать маленькому племяннику. M lle Bourienne тоже, как казалось, страстно любила мальчика, и княжна Марья, часто лишая себя, уступала своей подруге наслаждение нянчить маленького ангела (как называла она племянника) и играть с ним.
У алтаря лысогорской церкви была часовня над могилой маленькой княгини, и в часовне был поставлен привезенный из Италии мраморный памятник, изображавший ангела, расправившего крылья и готовящегося подняться на небо. У ангела была немного приподнята верхняя губа, как будто он сбирался улыбнуться, и однажды князь Андрей и княжна Марья, выходя из часовни, признались друг другу, что странно, лицо этого ангела напоминало им лицо покойницы. Но что было еще страннее и чего князь Андрей не сказал сестре, было то, что в выражении, которое дал случайно художник лицу ангела, князь Андрей читал те же слова кроткой укоризны, которые он прочел тогда на лице своей мертвой жены: «Ах, зачем вы это со мной сделали?…»
Вскоре после возвращения князя Андрея, старый князь отделил сына и дал ему Богучарово, большое имение, находившееся в 40 верстах от Лысых Гор. Частью по причине тяжелых воспоминаний, связанных с Лысыми Горами, частью потому, что не всегда князь Андрей чувствовал себя в силах переносить характер отца, частью и потому, что ему нужно было уединение, князь Андрей воспользовался Богучаровым, строился там и проводил в нем большую часть времени.
Князь Андрей, после Аустерлицкой кампании, твердо pешил никогда не служить более в военной службе; и когда началась война, и все должны были служить, он, чтобы отделаться от действительной службы, принял должность под начальством отца по сбору ополчения. Старый князь с сыном как бы переменились ролями после кампании 1805 года. Старый князь, возбужденный деятельностью, ожидал всего хорошего от настоящей кампании; князь Андрей, напротив, не участвуя в войне и в тайне души сожалея о том, видел одно дурное.
26 февраля 1807 года, старый князь уехал по округу. Князь Андрей, как и большею частью во время отлучек отца, оставался в Лысых Горах. Маленький Николушка был нездоров уже 4 й день. Кучера, возившие старого князя, вернулись из города и привезли бумаги и письма князю Андрею.
Камердинер с письмами, не застав молодого князя в его кабинете, прошел на половину княжны Марьи; но и там его не было. Камердинеру сказали, что князь пошел в детскую.
– Пожалуйте, ваше сиятельство, Петруша с бумагами пришел, – сказала одна из девушек помощниц няни, обращаясь к князю Андрею, который сидел на маленьком детском стуле и дрожащими руками, хмурясь, капал из стклянки лекарство в рюмку, налитую до половины водой.
– Что такое? – сказал он сердито, и неосторожно дрогнув рукой, перелил из стклянки в рюмку лишнее количество капель. Он выплеснул лекарство из рюмки на пол и опять спросил воды. Девушка подала ему.
В комнате стояла детская кроватка, два сундука, два кресла, стол и детские столик и стульчик, тот, на котором сидел князь Андрей. Окна были завешаны, и на столе горела одна свеча, заставленная переплетенной нотной книгой, так, чтобы свет не падал на кроватку.
– Мой друг, – обращаясь к брату, сказала княжна Марья от кроватки, у которой она стояла, – лучше подождать… после…
– Ах, сделай милость, ты всё говоришь глупости, ты и так всё дожидалась – вот и дождалась, – сказал князь Андрей озлобленным шопотом, видимо желая уколоть сестру.
– Мой друг, право лучше не будить, он заснул, – умоляющим голосом сказала княжна.
Князь Андрей встал и, на цыпочках, с рюмкой подошел к кроватке.
– Или точно не будить? – сказал он нерешительно.
– Как хочешь – право… я думаю… а как хочешь, – сказала княжна Марья, видимо робея и стыдясь того, что ее мнение восторжествовало. Она указала брату на девушку, шопотом вызывавшую его.
Была вторая ночь, что они оба не спали, ухаживая за горевшим в жару мальчиком. Все сутки эти, не доверяя своему домашнему доктору и ожидая того, за которым было послано в город, они предпринимали то то, то другое средство. Измученные бессоницей и встревоженные, они сваливали друг на друга свое горе, упрекали друг друга и ссорились.
– Петруша с бумагами от папеньки, – прошептала девушка. – Князь Андрей вышел.
– Ну что там! – проговорил он сердито, и выслушав словесные приказания от отца и взяв подаваемые конверты и письмо отца, вернулся в детскую.
– Ну что? – спросил князь Андрей.
– Всё то же, подожди ради Бога. Карл Иваныч всегда говорит, что сон всего дороже, – прошептала со вздохом княжна Марья. – Князь Андрей подошел к ребенку и пощупал его. Он горел.
– Убирайтесь вы с вашим Карлом Иванычем! – Он взял рюмку с накапанными в нее каплями и опять подошел.
– Andre, не надо! – сказала княжна Марья.
Но он злобно и вместе страдальчески нахмурился на нее и с рюмкой нагнулся к ребенку. – Ну, я хочу этого, сказал он. – Ну я прошу тебя, дай ему.
Княжна Марья пожала плечами, но покорно взяла рюмку и подозвав няньку, стала давать лекарство. Ребенок закричал и захрипел. Князь Андрей, сморщившись, взяв себя за голову, вышел из комнаты и сел в соседней, на диване.
Письма всё были в его руке. Он машинально открыл их и стал читать. Старый князь, на синей бумаге, своим крупным, продолговатым почерком, употребляя кое где титлы, писал следующее:
«Весьма радостное в сей момент известие получил через курьера, если не вранье. Бенигсен под Эйлау над Буонапартием якобы полную викторию одержал. В Петербурге все ликуют, e наград послано в армию несть конца. Хотя немец, – поздравляю. Корчевский начальник, некий Хандриков, не постигну, что делает: до сих пор не доставлены добавочные люди и провиант. Сейчас скачи туда и скажи, что я с него голову сниму, чтобы через неделю всё было. О Прейсиш Эйлауском сражении получил еще письмо от Петиньки, он участвовал, – всё правда. Когда не мешают кому мешаться не следует, то и немец побил Буонапартия. Сказывают, бежит весьма расстроен. Смотри ж немедля скачи в Корчеву и исполни!»
Князь Андрей вздохнул и распечатал другой конверт. Это было на двух листочках мелко исписанное письмо от Билибина. Он сложил его не читая и опять прочел письмо отца, кончавшееся словами: «скачи в Корчеву и исполни!» «Нет, уж извините, теперь не поеду, пока ребенок не оправится», подумал он и, подошедши к двери, заглянул в детскую. Княжна Марья всё стояла у кроватки и тихо качала ребенка.
«Да, что бишь еще неприятное он пишет? вспоминал князь Андрей содержание отцовского письма. Да. Победу одержали наши над Бонапартом именно тогда, когда я не служу… Да, да, всё подшучивает надо мной… ну, да на здоровье…» и он стал читать французское письмо Билибина. Он читал не понимая половины, читал только для того, чтобы хоть на минуту перестать думать о том, о чем он слишком долго исключительно и мучительно думал.
Билибин находился теперь в качестве дипломатического чиновника при главной квартире армии и хоть и на французском языке, с французскими шуточками и оборотами речи, но с исключительно русским бесстрашием перед самоосуждением и самоосмеянием описывал всю кампанию. Билибин писал, что его дипломатическая discretion [скромность] мучила его, и что он был счастлив, имея в князе Андрее верного корреспондента, которому он мог изливать всю желчь, накопившуюся в нем при виде того, что творится в армии. Письмо это было старое, еще до Прейсиш Эйлауского сражения.
«Depuis nos grands succes d'Austerlitz vous savez, mon cher Prince, писал Билибин, que je ne quitte plus les quartiers generaux. Decidement j'ai pris le gout de la guerre, et bien m'en a pris. Ce que j'ai vu ces trois mois, est incroyable.
«Je commence ab ovo. L'ennemi du genre humain , comme vous savez, s'attaque aux Prussiens. Les Prussiens sont nos fideles allies, qui ne nous ont trompes que trois fois depuis trois ans. Nous prenons fait et cause pour eux. Mais il se trouve que l'ennemi du genre humain ne fait nulle attention a nos beaux discours, et avec sa maniere impolie et sauvage se jette sur les Prussiens sans leur donner le temps de finir la parade commencee, en deux tours de main les rosse a plate couture et va s'installer au palais de Potsdam.
«J'ai le plus vif desir, ecrit le Roi de Prusse a Bonaparte, que V. M. soit accueillie еt traitee dans mon palais d'une maniere, qui lui soit agreable et c'est avec еmpres sement, que j'ai pris a cet effet toutes les mesures que les circonstances me permettaient. Puisse je avoir reussi! Les generaux Prussiens se piquent de politesse envers les Francais et mettent bas les armes aux premieres sommations.
«Le chef de la garienison de Glogau avec dix mille hommes, demande au Roi de Prusse, ce qu'il doit faire s'il est somme de se rendre?… Tout cela est positif.
«Bref, esperant en imposer seulement par notre attitude militaire, il se trouve que nous voila en guerre pour tout de bon, et ce qui plus est, en guerre sur nos frontieres avec et pour le Roi de Prusse . Tout est au grand complet, il ne nous manque qu'une petite chose, c'est le general en chef. Comme il s'est trouve que les succes d'Austerlitz aurant pu etre plus decisifs si le general en chef eut ete moins jeune, on fait la revue des octogenaires et entre Prosorofsky et Kamensky, on donne la preference au derienier. Le general nous arrive en kibik a la maniere Souvoroff, et est accueilli avec des acclamations de joie et de triomphe.
«Le 4 arrive le premier courrier de Petersbourg. On apporte les malles dans le cabinet du Marieechal, qui aime a faire tout par lui meme. On m'appelle pour aider a faire le triage des lettres et prendre celles qui nous sont destinees. Le Marieechal nous regarde faire et attend les paquets qui lui sont adresses. Nous cherchons – il n'y en a point. Le Marieechal devient impatient, se met lui meme a la besogne et trouve des lettres de l'Empereur pour le comte T., pour le prince V. et autres. Alors le voila qui se met dans une de ses coleres bleues. Il jette feu et flamme contre tout le monde, s'empare des lettres, les decachete et lit celles de l'Empereur adressees a d'autres. А, так со мною поступают! Мне доверия нет! А, за мной следить велено, хорошо же; подите вон! Et il ecrit le fameux ordre du jour au general Benigsen
«Я ранен, верхом ездить не могу, следственно и командовать армией. Вы кор д'арме ваш привели разбитый в Пултуск: тут оно открыто, и без дров, и без фуража, потому пособить надо, и я так как вчера сами отнеслись к графу Буксгевдену, думать должно о ретираде к нашей границе, что и выполнить сегодня.
«От всех моих поездок, ecrit il a l'Empereur, получил ссадину от седла, которая сверх прежних перевозок моих совсем мне мешает ездить верхом и командовать такой обширной армией, а потому я командованье оной сложил на старшего по мне генерала, графа Буксгевдена, отослав к нему всё дежурство и всё принадлежащее к оному, советовав им, если хлеба не будет, ретироваться ближе во внутренность Пруссии, потому что оставалось хлеба только на один день, а у иных полков ничего, как о том дивизионные командиры Остерман и Седморецкий объявили, а у мужиков всё съедено; я и сам, пока вылечусь, остаюсь в гошпитале в Остроленке. О числе которого ведомость всеподданнейше подношу, донеся, что если армия простоит в нынешнем биваке еще пятнадцать дней, то весной ни одного здорового не останется.
«Увольте старика в деревню, который и так обесславлен остается, что не смог выполнить великого и славного жребия, к которому был избран. Всемилостивейшего дозволения вашего о том ожидать буду здесь при гошпитале, дабы не играть роль писарскую , а не командирскую при войске. Отлучение меня от армии ни малейшего разглашения не произведет, что ослепший отъехал от армии. Таковых, как я – в России тысячи».
«Le Marieechal se fache contre l'Empereur et nous punit tous; n'est ce pas que с'est logique!
«Voila le premier acte. Aux suivants l'interet et le ridicule montent comme de raison. Apres le depart du Marieechal il se trouve que nous sommes en vue de l'ennemi, et qu'il faut livrer bataille. Boukshevden est general en chef par droit d'anciennete, mais le general Benigsen n'est pas de cet avis; d'autant plus qu'il est lui, avec son corps en vue de l'ennemi, et qu'il veut profiter de l'occasion d'une bataille „aus eigener Hand“ comme disent les Allemands. Il la donne. C'est la bataille de Poultousk qui est sensee etre une grande victoire, mais qui a mon avis ne l'est pas du tout. Nous autres pekins avons, comme vous savez, une tres vilaine habitude de decider du gain ou de la perte d'une bataille. Celui qui s'est retire apres la bataille, l'a perdu, voila ce que nous disons, et a ce titre nous avons perdu la bataille de Poultousk. Bref, nous nous retirons apres la bataille, mais nous envoyons un courrier a Petersbourg, qui porte les nouvelles d'une victoire, et le general ne cede pas le commandement en chef a Boukshevden, esperant recevoir de Petersbourg en reconnaissance de sa victoire le titre de general en chef. Pendant cet interregne, nous commencons un plan de man?uvres excessivement interessant et original. Notre but ne consiste pas, comme il devrait l'etre, a eviter ou a attaquer l'ennemi; mais uniquement a eviter le general Boukshevden, qui par droit d'ancnnete serait notre chef. Nous poursuivons ce but avec tant d'energie, que meme en passant une riviere qui n'est рas gueable, nous brulons les ponts pour nous separer de notre ennemi, qui pour le moment, n'est pas Bonaparte, mais Boukshevden. Le general Boukshevden a manque etre attaque et pris par des forces ennemies superieures a cause d'une de nos belles man?uvres qui nous sauvait de lui. Boukshevden nous poursuit – nous filons. A peine passe t il de notre cote de la riviere, que nous repassons de l'autre. A la fin notre ennemi Boukshevden nous attrappe et s'attaque a nous. Les deux generaux se fachent. Il y a meme une provocation en duel de la part de Boukshevden et une attaque d'epilepsie de la part de Benigsen. Mais au moment critique le courrier, qui porte la nouvelle de notre victoire de Poultousk, nous apporte de Petersbourg notre nomination de general en chef, et le premier ennemi Boukshevden est enfonce: nous pouvons penser au second, a Bonaparte. Mais ne voila t il pas qu'a ce moment se leve devant nous un troisieme ennemi, c'est le православное qui demande a grands cris du pain, de la viande, des souchary, du foin, – que sais je! Les magasins sont vides, les сhemins impraticables. Le православное se met a la Marieaude, et d'une maniere dont la derieniere campagne ne peut vous donner la moindre idee. La moitie des regiments forme des troupes libres, qui parcourent la contree en mettant tout a feu et a sang. Les habitants sont ruines de fond en comble, les hopitaux regorgent de malades, et la disette est partout. Deux fois le quartier general a ete attaque par des troupes de Marieaudeurs et le general en chef a ete oblige lui meme de demander un bataillon pour les chasser. Dans une de ces attaques on m'a еmporte ma malle vide et ma robe de chambre. L'Empereur veut donner le droit a tous les chefs de divisions de fusiller les Marieaudeurs, mais je crains fort que cela n'oblige une moitie de l'armee de fusiller l'autre.