Квадратное уравнение
Квадра́тное уравне́ние — алгебраическое уравнение общего вида
- <math>ax^2 + bx + c = 0,</math>
где <math>x</math> — свободная переменная, <math>a</math>, <math>b</math>, <math>c</math> — коэффициенты, причём <math>\quad a \ne 0.</math>
Выражение <math>ax^2+bx+c</math> называют квадратным трёхчленом[1].
Корень — это значение переменной <math>x</math>, обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное равенство.
Элементы квадратного уравнения имеют собственные названия[1]:
- <math>a</math> называют первым или старшим коэффициентом,
- <math>b</math> называют вторым, средним или коэффициентом при <math>x</math>,
- <math>c</math> называют свободным членом.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент <math>a</math>:
- <math>x^2 + px + q = 0, \quad p=\frac{b}{a}, \quad q=\frac{c}{a}.</math>
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.
Содержание
- 1 Исторические сведения о квадратных уравнениях
- 2 Корни квадратного уравнения на множестве действительных чисел
- 2.1 I способ. Общая формула для вычисления корней
- 2.2 II способ. Корни квадратного уравнения при чётном коэффициенте b
- 2.3 III способ. Решение неполных квадратных уравнений
- 2.4 IV способ. Использование частных соотношений коэффициентов
- 2.5 V способ. Разложение квадратного трёхчлена на линейные множители
- 2.6 VI способ. Использование прямой и обратной теоремы Виета
- 2.7 VII способ. Метод «переброски»
- 3 Геометрический смысл
- 4 Корни квадратного уравнения на множестве комплексных чисел
- 5 Корни приведённого квадратного уравнения
- 6 Теорема Виета
- 7 Разложение квадратного трёхчлена на множители и теоремы, следующие из этого
- 8 Уравнения, сводящиеся к квадратным
- 9 Примечания
- 10 Литература
- 11 Ссылки
Исторические сведения о квадратных уравнениях
Древний Вавилон
Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения[1]. Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведём примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:
- <math>x^2+x=\frac{3}{4};\ x^2-x=14\frac{1}{2}.</math>
Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путём которых эти правила были получены.
Индия
Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.)[1]; Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: <math>ax^2+bx=c</math>; притом предполагалось, что в нём все коэффициенты, кроме <math>a,</math> могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным.
Корни квадратного уравнения на множестве действительных чисел
I способ. Общая формула для вычисления корней
Для нахождения корней квадратного уравнения <math> ax^2 + bx +c=0</math> в общем случае следует пользоваться приводимым ниже алгоритмом:
| Условие | <math>D > 0</math> | <math>D = 0</math> | <math>D < 0</math> |
| Число действительных корней | корней два | корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях — его, к тому же, называют корнем кратности 2) | делают вывод о том, что корней на множестве действительных чисел нет. |
| Формула | <math>x_1 = x_2 = -\frac{b}{2a}</math> |
формулу комплексных корней смотрите ниже в соотв. разделе |
Примечание: очевидно, что формула для корня кратности 2 является частным случаем общей формулы, получается при подстановке в неё равенства D=0, а вывод о отсутствии вещественных корней при D<0 следует также сделать, учтя, что в этом случае -D>0, а <math>\sqrt{-1}=i</math>. }}
Изложенный метод универсален, однако он далеко не единственный. К решению одного уравнения можно подойти различными способами, предпочтения обычно зависят от самого решающего. Кроме того, часто для этого некоторый из способов оказывается значительно более элегантным, простым, менее трудоёмким, чем стандартный.
II способ. Корни квадратного уравнения при чётном коэффициенте b
Для уравнений вида <math>ax^2 + 2kx + c = 0</math>, то есть при чётном <math>b</math>, где
- <math>k=\frac{1}{2}b,</math>
вместо формулы (1) для нахождения корней можно использовать более простые выражения[1].
Примечание: данные ниже формулы можно получить, подставив в стандартные формулы выражение b=2k и совершив при этом несложные преобразования.
| неприведённое | приведённое | D>0 | неприведённое | приведённое |
| удобнее вычислять значение
четверти дискриминанта:
Все необходимые свойства при этом сохраняются. |
<math>\frac{D}{4}=k^2-c</math>. | <math>x_{1, 2}=\frac{-k\pm\sqrt{k^2-ac}}{a}.</math> | <math>x_{1,2}=-k\pm\sqrt{k^2-c}</math> | |
| D=0 | <math>x=\frac{-k}{a}</math> | <math>x=-k</math> | ||
III способ. Решение неполных квадратных уравнений
К решению неполных квадратных уравнений следует подходить по-особому. Рассмотрим три возможных ситуации.
| <math>ax^2=0;</math>
<math>x^2=0;</math> <math>x=0.</math>
|
<math>ax^2+c=0</math>
<math>ax^2=-c;</math> <math>x^2=-\frac{c}{a};</math> <math>x_{1, 2}=\pm\sqrt{-\frac{c}{a}}.</math> Если <math>-\frac{c}{a}>0;</math>, то уравнение имеет два действительных корня, если <math>-\frac{c}{a}=0;</math>, то <math>x=0.</math>, a если <math>-\frac{c}{a}<0;</math>, то уравнение не имеет действительных корней. |
<math>ax^2+bx=0;</math>
<math>x(ax+b)=0;</math> <math>x=0</math> или <math>ax+b=0;</math> <math>x=-\frac{b}{a}.</math> Такое уравнение обязательно имеет два действительных корня |
IV способ. Использование частных соотношений коэффициентов
Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.
Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту
Если в квадратном уравнении <math>ax^2+bx+c=0</math> сумма первого коэффициента и свободного члена равна второму коэффициенту: <math>a+c=b</math>, то его корнями являются <math>-1</math> и число, противоположное отношению свободного члена к старшему коэффициенту (<math>-\frac{c}{a}</math>).
- <math>x_1=\frac{-a-c-a+c}{2a}=\frac{-2a}{2a}=-1;</math>
- <math>x_2=\frac{-a-c+a-c}{2a}=\frac{-2c}{2a}=-\frac{c}{a}.</math>
В частности, если <math>a=c</math>, то корень будет один: <math>-1.</math>
Способ 2.  Используем геометрическую модель корней квадратного уравнения: их мы будем рассматривать как точки пересечения параболы <math>y=ax^2 +bx+c</math> с осью абсцисс. Всякая парабола вне зависимости от задающего её выражения является фигурой, симметричной относительно прямой <math>x=-\frac{b}{2a}</math>. Это означает, что отрезок всякой перпендикулярной к ней прямой, отсекаемый на ней параболой, делится осью симметрии пополам. Сказанное, в частности, верно и для оси абсцисс. Таким образом, для всякой параболы справедливо одно из следующих равенств: <math> -\frac{b}{2a} + \rho (x_1; -\frac{b}{2a})=x_2</math> (если <math> x_1<x_2</math>) или <math> -\frac{b}{2a} - \rho (-\frac{b}{2a}; x_1)=x_2</math> (если верно неравенство противоположного смысла). Используя тождество <math>\rho(a;b)=|a-b|</math>, выражающее геометрический смысл модуля, а также принимая, что <math>x_1=-1</math> (это можно доказать, подставив равенство в квадратный трёхчлен: <math> a \cdot (-1)^2 + b \cdot (-1) + c = (a+c)-b=0</math>, поэтому -1 - корень такого уравнения) , приходим к следующему равенству: <math>-\frac{b}{2a} \pm |-\frac{b}{2a}-(-1)| = x_2.</math> Если учитывать, что разность в том случае, когда мы прибавляем модуль, всегда положительна, а в том, когда отнимаем - отрицательна, что говорит о тождественности этих случаев, и, к тому же, помня о равенстве <math>b-a=c</math>, раскрываем модуль: <math>x_2=-\frac{b}{2a} -\frac{b}{2a}+1=-\frac{2b-2a}{2a}=-\frac{b-a}{a}=-\frac{c}{a}</math>. Во втором случае,совершив аналогичные преобразования, придём к тому же результату, ч.т.д.
}}
Используем геометрическую модель корней квадратного уравнения: их мы будем рассматривать как точки пересечения параболы <math>y=ax^2 +bx+c</math> с осью абсцисс. Всякая парабола вне зависимости от задающего её выражения является фигурой, симметричной относительно прямой <math>x=-\frac{b}{2a}</math>. Это означает, что отрезок всякой перпендикулярной к ней прямой, отсекаемый на ней параболой, делится осью симметрии пополам. Сказанное, в частности, верно и для оси абсцисс. Таким образом, для всякой параболы справедливо одно из следующих равенств: <math> -\frac{b}{2a} + \rho (x_1; -\frac{b}{2a})=x_2</math> (если <math> x_1<x_2</math>) или <math> -\frac{b}{2a} - \rho (-\frac{b}{2a}; x_1)=x_2</math> (если верно неравенство противоположного смысла). Используя тождество <math>\rho(a;b)=|a-b|</math>, выражающее геометрический смысл модуля, а также принимая, что <math>x_1=-1</math> (это можно доказать, подставив равенство в квадратный трёхчлен: <math> a \cdot (-1)^2 + b \cdot (-1) + c = (a+c)-b=0</math>, поэтому -1 - корень такого уравнения) , приходим к следующему равенству: <math>-\frac{b}{2a} \pm |-\frac{b}{2a}-(-1)| = x_2.</math> Если учитывать, что разность в том случае, когда мы прибавляем модуль, всегда положительна, а в том, когда отнимаем - отрицательна, что говорит о тождественности этих случаев, и, к тому же, помня о равенстве <math>b-a=c</math>, раскрываем модуль: <math>x_2=-\frac{b}{2a} -\frac{b}{2a}+1=-\frac{2b-2a}{2a}=-\frac{b-a}{a}=-\frac{c}{a}</math>. Во втором случае,совершив аналогичные преобразования, придём к тому же результату, ч.т.д.
}}
- Отсюда, прежде, чем решать какое-либо квадратное уравнение, следует проверить возможность применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.
Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю
Если в квадратном уравнении сумма всех его коэффициентов равна нулю (<math>a+b+c=0</math>), то корнями такого уравнения являются <math>1</math> и отношение свободного члена к старшему коэффициенту (<math>\frac{c}{a}</math>).
- <math>x_1=\frac{a+c+a-c}{2a}=\frac{2a}{2a}=1;</math>
- <math>x_2=\frac{a+c-a+c}{2a}=\frac{2c}{2a}=\frac{c}{a},</math>
что и требовалось доказать.
- В частности, если <math>a=c</math>, то уравнение имеет только один корень, которым является число <math>1</math>.
Способ 2. Пользуясь данным выше определением корня квадратного уравнения, обнаруживаем путём подстановки, что число 1 является таковым в рассматриваемом случае: <math>a \cdot 1^2 + b \cdot 1 + c =0</math> - верное равенство, следовательно, единица - корень такого вида квадратных уравнений. Далее, по теореме Виета находим второй корень: согласно этой теореме, произведение корней уравнения равно числу, равному отношению свободного члена к старшему коэффициенту - <math>x_1 x_2 =\frac{c}{a} \Rightarrow x_2 =\frac{c}{ax_1}=\frac{c}{a \cdot 1} =\frac{c}{a}</math>, ч.т.д. }}
- Отсюда, прежде, чем решать уравнение стандартными методами, следует проверить применимость к нему этой теоремы: сложить все коэффициенты данного уравнения и посмотреть, не равна ли нулю эта сумма.
V способ. Разложение квадратного трёхчлена на линейные множители
Если трёхчлен вида <math> ax^2 + bx +c (a\not=0) </math> удастся каким-либо образом представить в качестве произведения линейных множителей <math>(kx+m)(lx+n)=0</math>, то можно найти корни уравнения <math> ax^2 + bx +c=0</math> — ими будут <math> -\frac{m}{k}</math> и <math>-\frac{n}{l}</math>, действительно, ведь <math>(kx+m)(lx+n)=0 \Longleftrightarrow kx+m=0 \cup lx+n=0</math>, а решив указанные линейные уравнения, получим вышеописанное. Отметим, что квадратный трёхчлен не всегда раскладывается на линейные множители с действительными коэффициентами: это возможно, если соответствующее ему уравнение имеет действительные корни.
Рассмотрим некоторые частные случаи.
Использование формулы квадрата суммы (разности)
Если квадратный трёхчлен имеет вид <math>(ax)^2 +2abx+b^2</math>, то применив к нему названную формулу, мы сможем разложить его на линейные множители и, значит, найти корни:
- <math>(ax)^2 +2abx + b^2 = (ax+b)^2;</math>
- <math>(ax+b)^2 = 0;</math>
- <math>x=-\frac{b}{a}.</math>
Выделение полного квадрата суммы (разности)
Также названную формулу применяют, пользуясь методом, получившим названия «выделение полного квадрата суммы (разности)». Применительно к приведённому квадратному уравнению с введёнными ранее обозначениями, это означает следующее:
- прибавляют и отнимают одно и то же число
<math>x^2 +px+(\frac{p}{2})^2 - (\frac{p}{2})^2 +q =0;</math>. - применяют формулу к полученному выражению, переносят вычитаемое и свободный член в правую часть
<math>(x^2 + 2\frac{p}{2}x +(\frac{p}{2})^2) + (- (\frac{p}{2})^2 +q)=0;</math>
<math>(x+\frac{p}{2})^2=\frac{p^2}{4}-q;</math> - извлекают из левой и правой частей уравнения квадратный корень и выражают переменную
<math>x+\frac{p}{2}=\pm\sqrt {\frac{p^2}{4}-q};</math>
<math>x_{1, 2}=-\frac{p}{2}\pm\sqrt {\frac{p^2}{4}-q}. </math>
Примечание: если вы заметили, данная формула совпадает с предлагаемой в разделе «Корни приведённого квадратного уравнения», которую, в свою очередь, можно получить из общей формулы (1) путём подстановки равенства a=1. Этот факт не просто совпадение: описанным методом, произведя, правда некоторые дополнительные рассуждения, можно вывести и общую формулу, а также доказать свойства дискриминанта.
VI способ. Использование прямой и обратной теоремы Виета
Прямая теорема Виета (см. ниже в одноимённом разделе) и обратная ей теорема позволяют решать приведённые квадратные уравнения устно, не прибегая к достаточно громоздким вычислениям по формуле (1).
Согласно обратной теореме, всякая пара чисел (число) <math>x_1 , x_2</math>, будучи решением нижеприведённой системы уравнений, являются корнями уравнения <math>x^2 + px +q=0</math>:
- <math> \begin{cases} x_1 + x_2 = -p;\\ x_1 x_2 = q; \end{cases}</math>
Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С её помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:
- 1) если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;
- 2) если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.
VII способ. Метод «переброски»
Так называемый метод «переброски» позволяет сводить решение неприведённых и непреобразуемых к виду приведённых с целыми коэффициентами путём их деления на старший коэффициент уравнений к решению приведённых с целыми коэффициентами. Он заключается в следующем:
- 1) умножаем обе части на выражение:
- <math>ax^2+bx+c=0|\cdot a</math>
- <math>(ax)^2 +b(ax)+ac=0</math>
- 2) вводим новую переменную y=ax:
- <math>y^2+by + ac</math>.
Далее уравнение решают устно описанным выше способом, затем возвращаются к исходной переменной и находят корни уравнений <math>y_1=ax_1</math> и <math>y_2=ax_2</math>.
Геометрический смысл
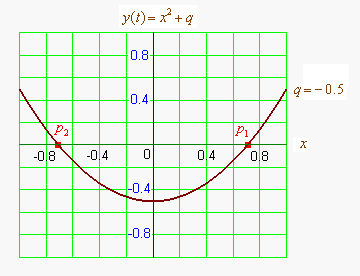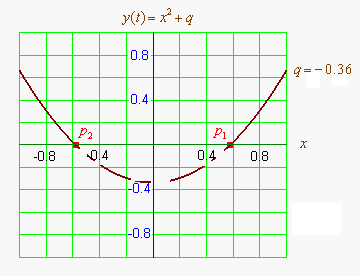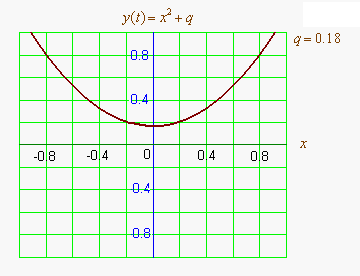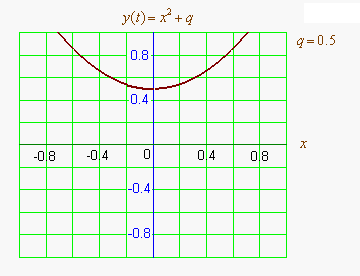 Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня (см. изображение справа.)
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня (см. изображение справа.)
Если коэффициент <math>a</math> положительный, ветви параболы направлены вверх и наоборот. Если коэффициент <math>b</math> положительный (при положительном <math>a</math>, при отрицательном наоборот), то вершина параболы лежит в левой полуплоскости и наоборот.
Графический способ решения квадратных уравнений
Помимо универсального способа, описанного выше, существует так называемый графический способ. В общем виде этот способ решения рационального уравнения вида <math>f(x)=g(x)</math> заключается в следующем: в одной системе координат строят графики функций <math>y=f(x)</math> и <math>y=g(x)</math> и находят абсциссы общих точек этих графиков; найденные числа и будут корнями уравнения.
- Есть всего пять основных способов графического решения квадратных уравнений.
Способ I
Для решения квадратного уравнения <math>ax^2+bx+c=0</math> этим способом строится график функции <math>y=ax^2+bx+c</math> и отыскивается абсциссы точек пересечения такого графика с осью <math>x</math>.
Способ II
Для решения того же уравнения этим способом его преобразуют к виду <math>ax^2=-bx-c</math> и строят в одной системе координат графики квадратичной функции <math>y=ax^2</math> и линейной функции <math>y=-bx-c</math>, затем находят абсциссу точек их пересечения.
Способ III
Решение этим методом подразумевает преобразование исходного уравнения к виду <math>a(x+l)^2+m=0</math>, используя метод выделения полного квадрата суммы (разности) и затем в <math>a(x+l)^2=-m</math>. После этого строятся график функции <math>y=a(x+l)^2</math> (им является график функции <math>y=ax^2</math>, смещённый на <math>|l|</math> единиц масштаба в право или влево в зависимости от знака) и прямую <math>y=-m</math>, параллельную оси абсцисс. Корнями уравнения будут абсциссы точек пересечения параболы и прямой.
Способ IV
Квадратное уравнение преобразуют к виду <math>ax^2+c=-bx</math>, строят график функции <math>y=ax^2+c</math> (им является график функции <math>y=ax^2</math>, смещённый на <math>c</math> единиц масштаба вверх, если этот коэффициент положителен, либо вниз если он отрицателен), и <math>y=-bx</math>, находят абсциссы их общих точек.
Способ V
Квадратное уравнение преобразуют к особому виду:
- <math>\frac{ax^2}{x}+\frac{bx}{x}+\frac{c}{x}=\frac{0}{x};</math>
- <math>ax+b+\frac{c}{x}=0;</math>
затем
- <math>ax+b=-\frac{c}{x}.</math>.
Совершив преобразования, строят графики линейной функции <math>y=ax+b</math> и обратной пропорциональности <math>y=-\frac{c}{x};\ (c\not=0)</math>, отыскивают абсциссы точек пересечения этих графиков. Этот метод имеет границу применимости: если <math>c=0</math>, то метод не используется.
Решение квадратных уравнений с помощью циркуля и линейки
Описанные выше методы графического решения имеют существенные недостатки: они достаточно трудоёмки, при этом точность построения кривых — парабол и гипербол — низка. Указанные проблемы не присущи предлагаемому ниже методу, предполагающему относительно более точные построения циркулем и линейкой.
Чтобы произвести такое решение, нужно выполнить нижеследующую последовательность действий.
- Построить в системе координат Oxy окружность с центром в точке <math>S(-\frac{b}{2a}; \frac{a+c}{2a})</math>, пересекающую ось y в точке C(0;1).
- Далее возможны три случая:
- длина радиуса окружности превышает длину перпендикуляра к оси абсцисс, опущенного из точки S: в этом случае окружность пересекает ось x в двух точках, а уравнение имеет два действительных корня, равных абсциссам этих точек;
- радиус равен перпендикуляру: одна точка и один вещественный корень кратности 2;
- радиус меньше перпендикуляра: корней в множестве <math>\mathbb R</math> нет.
Итак, нами найдены необходимые для построения данные. Действительно, если мы построим окружность с центром в точке <math>S(-\frac{b}{2a}; \frac{c+a}{2a})</math>, проходящую через точку <math>C(0; 1)</math>, то она, в случаях, когда уравнение имеет действительные корни, пересечёт ось x в точках, абсциссы которых есть эти корни. Причём, если длина радиуса больше длины перпендикуляра к оси Ox, то уравнение имеет два корня (предположив обратное, мы бы получили противоречие с доказанным выше), если длины равны, то один (по той же причине), если же длина радиуса меньше длины перпендикуляра, то окружность не имеет общих точек с осью x, следовательно, и действительных корней у уравнения нет (доказывается тоже от противного: если корни есть, то окружность, проходящая через A, B, C совпадает с данной, и поэтому пересекает ось, однако она не должна пересекать ось абсцисс по условию, значит, предположение неверно). }}
Корни квадратного уравнения на множестве комплексных чисел
Уравнение с действительными коэффициентами
Квадратное уравнение с вещественными коэффициентами <math>a,~b,~c</math> имеет ровно два комплексных корня, о чём гласит основная теорема алгебры. При этом, в зависимости от значения дискриминанта <math>D=b^2 - 4ac</math>, как один, так и оба корня могут не иметь мнимой части и быть вещественными:
- при <math>D > 0</math> вещественных корней два, и они вычисляются по формуле
- <math>x_{1,2} = \frac{-b \pm \sqrt{D}}{2a};</math>
- при <math>D = 0</math> корень один (о чём так же можно говорить как о двух равных или совпадающих корнях), кратности 2:
- <math>x = \frac{-b \pm 0}{2a} = \frac{-b}{2a};</math>
- при <math>D < 0</math> вещественных (действительных) корней нет, однако существуют два комплексных корня, выражающиеся той же формулой, что и для положительного дискриминанта. Также её можно переписать, выразив корень из отрицательного числа в виде произведения корня с мнимой единицей:
- <math>x_{1,2} = \frac{-b \pm i\sqrt{|D|}}{2a}.</math>
Уравнение с комплексными коэффициентами
В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше её вариантам, но различимыми являются только два случая: нулевого дискриминанта (один двукратный корень) и ненулевого (два простых корня).
Корни приведённого квадратного уравнения
Квадратное уравнение вида <math>x^2 + px + q = 0,</math> в котором старший коэффициент <math>a</math> равен единице, называют приведённым. В этом случае формула для корней (1) упрощается до
- <math>x_{1,2}= -\frac p2 \pm \sqrt{\left( \frac p2 \right)^2-q}.</math>
Мнемонические правила:
- Из «Радионяни»:
«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
Сводится всё к пустяку:
p пополам и в квадрате
Минус прекрасное[2] q.
- Из «Радионяни» (другой вариант):
p, со знаком взяв обратным,
На два мы его разделим,
И от корня аккуратно
Знаком «минус-плюс» отделим.
А под корнем очень кстати
Половина p в квадрате
Минус q — и вот решенья,
То есть корни уравненья.
Теорема Виета
Формулировка
Сумма корней приведённого квадратного уравнения <math>x^2 + px + q = 0</math> равна коэффициенту <math>p</math> со знаком «минус», а произведение корней равно свободному члену <math>q</math>
- <math>x_1 + x_2 = -p, \quad x_1x_2 = q.</math>
В общем случае, то есть для не приведённого квадратного уравнения <math>ax^2 + bx + c = 0</math>:
- <math>x_1 + x_2 = -b/a, \quad x_1x_2 = c/a.</math>
Используя эту теорему, можно решать некоторые квадратные уравнения устно.
Разложение квадратного трёхчлена на множители и теоремы, следующие из этого
Если известны оба корня квадратного трёхчлена, его можно разложить по формуле
- <math>ax^2+bx+c=a(x-x_1)(x-x_2)</math> (2)
Доказательство
Для доказательства этого утверждения воспользуемся теоремой Виета. Согласно этой теореме, корни <math>x_1</math> и <math>x_2</math> квадратного уравнения <math>ax^2+bx+c=0</math> образуют соотношения с его коэффициентами: <math>x_1+x_2=-\frac{b}{a};\ x_1x_2=\frac{c}{a}</math>. Подставим эти соотношения в квадратный трёхчлен:
- <math>ax^2+bx+c=a(x^2+\frac{b}{a}x+\frac{c}{a})=a(x^2-(x_1+x_2)x+x_1x_2)=</math>
- <math>=a(x^2-x_1x-x_2x+x_1x_2)=a(x(x-x_1)-x_2(x-x_1))=a(x-x_1)(x-x_2)</math>.
В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.
- Из формулы (2) имеются два важных следствия:
Следствие 1
- Если квадратный трёхчлен раскладывается на линейные множители с вещественными коэффициентами, то он имеет корни, принадлежащие тому числовому множеству.
Доказательство
Пусть <math>ax^2+bx+c=(kx+m)(nx+l)</math>. Тогда, переписав это разложение, получим:
- <math>(kx+m)(nx+l)=k(x+\frac{m}{k})n(x+\frac{l}{n})=kn(x-(-\frac{m}{k}))(x-(-\frac{l}{n}))</math>.
Сопоставив полученное выражение с формулой (2), находим, что корнями такого трёхчлена являются <math>-\frac{m}{k}</math> и <math>-\frac{l}{n}</math>. Так как коэффициенты вещественны, то и числа, противоположные их отношениям также являются элементами множества <math>\mathbb R</math>.
Следствие 2
- Если квадратный трёхчлен не имеет действительных корней, то он не раскладывается на линейные множители с вещественными коэффициентами.
Доказательство
Действительно, если мы предположим противное (что такой трёхчлен раскладывается на линейные множители), то, согласно следствию 1, он имеет корни в множестве <math>\mathbb R</math>, что противоречит условию, а потому наше предположение неверно, и такой трёхчлен не раскладывается на линейные множители.
Уравнения, сводящиеся к квадратным
Алгебраические
Уравнение вида <math>a \cdot f^2(x) + b \cdot f(x) + c = 0</math> является уравнением, сводящимся к квадратному.
В общем случае оно решается заменой <math>f(x)=t, t \in E(f)</math> c последующим решением квадратного уравнения <math>a \cdot t^2 + b \cdot t + c = 0</math>.
Также при решении можно обойтись без замены, решив совокупность двух уравнений:
- <math>f(x) = \frac {-b - \sqrt{b^2-4 \cdot a \cdot c}} {2a}</math> и
- <math>f(x) = \frac {-b + \sqrt{b^2-4 \cdot a \cdot c}} {2a}</math>
Если <math>f(x)=x^2</math>, то уравнение принимает вид:
- <math>ax^4+bx^2+c=0</math>
Такое уравнение называется биквадратным[3][1].
С помощью замены
- <math>y = x + \dfrac{k}{x}</math>
к квадратному уравнению сводится уравнение
- <math>a x^4 + b x^3 + c x^2 + k b x + k^2 a = 0,</math>
известное как возвратное или обобщённо-симметрическое уравнение[1].
Дифференциальные
Линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка
- <math>y + py' + qy = 0</math>
подстановкой <math>y = e^{kx}</math> сводится к характеристическому квадратному уравнению:
- <math>k^2 + pk + q = 0</math>
Если решения этого уравнения <math>k_1</math> и <math>k_2</math> не равны друг другу, то общее решение имеет вид:
- <math>y = Ae^{k_1 x} + Be^{k_2 x}</math>, где <math>A</math> и <math>B</math> — произвольные постоянные.
Для комплексных корней <math>k_{1,2} = k_r \pm k_i i</math> можно переписать общее решение, используя формулу Эйлера:
- <math>y = e^{k_r x} \left( A\cos{k_i x} + B\sin{k_i x} \right) = Ae^{k_r x} \cos(k_i x + \varphi)</math>
Если решения характеристического уравнения совпадают <math>k_1 = k_2 = k</math>, общее решение записывается в виде:
- <math>y = Axe^{kx} + Be^{kx}</math>
Уравнения такого типа часто встречаются в самых разнообразных задачах математики и физики, например, в теории колебаний или теории цепей переменного тока.
Напишите отзыв о статье "Квадратное уравнение"
Примечания
Литература
- Квадратное уравнение; Квадратный трёхчлен // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 133-136. — 352 с.
Ссылки
| |
Квадратное уравнение в Викиучебнике? |
|---|
- Weisstein, Eric W. [mathworld.wolfram.com/QuadraticEquation.html Quadratic Equation] (англ.) на сайте Wolfram MathWorld.
- [festival.1september.ru/articles/509366/ Вывод формулы корней полного квадратного уравнения. Решение приведённых квадратных уравнений и уравнений с чётным вторым коэффициентом] / Фестиваль педагогических идей «Открытый урок».
- [geekandnerd.org/quadratic-factoring-calculator/ Калькулятор квадратного уравнения].
<imagemap>: неверное или отсутствующее изображение |
Для улучшения этой статьи по математике желательно?:
|
| ||||||
Отрывок, характеризующий Квадратное уравнение
«Горести, видно, общий удел наш, милый и нежный друг Julieie».«Ваша потеря так ужасна, что я иначе не могу себе объяснить ее, как особенную милость Бога, Который хочет испытать – любя вас – вас и вашу превосходную мать. Ах, мой друг, религия, и только одна религия, может нас, уже не говорю утешить, но избавить от отчаяния; одна религия может объяснить нам то, чего без ее помощи не может понять человек: для чего, зачем существа добрые, возвышенные, умеющие находить счастие в жизни, никому не только не вредящие, но необходимые для счастия других – призываются к Богу, а остаются жить злые, бесполезные, вредные, или такие, которые в тягость себе и другим. Первая смерть, которую я видела и которую никогда не забуду – смерть моей милой невестки, произвела на меня такое впечатление. Точно так же как вы спрашиваете судьбу, для чего было умирать вашему прекрасному брату, точно так же спрашивала я, для чего было умирать этому ангелу Лизе, которая не только не сделала какого нибудь зла человеку, но никогда кроме добрых мыслей не имела в своей душе. И что ж, мой друг, вот прошло с тех пор пять лет, и я, с своим ничтожным умом, уже начинаю ясно понимать, для чего ей нужно было умереть, и каким образом эта смерть была только выражением бесконечной благости Творца, все действия Которого, хотя мы их большею частью не понимаем, суть только проявления Его бесконечной любви к Своему творению. Может быть, я часто думаю, она была слишком ангельски невинна для того, чтобы иметь силу перенести все обязанности матери. Она была безупречна, как молодая жена; может быть, она не могла бы быть такою матерью. Теперь, мало того, что она оставила нам, и в особенности князю Андрею, самое чистое сожаление и воспоминание, она там вероятно получит то место, которого я не смею надеяться для себя. Но, не говоря уже о ней одной, эта ранняя и страшная смерть имела самое благотворное влияние, несмотря на всю печаль, на меня и на брата. Тогда, в минуту потери, эти мысли не могли притти мне; тогда я с ужасом отогнала бы их, но теперь это так ясно и несомненно. Пишу всё это вам, мой друг, только для того, чтобы убедить вас в евангельской истине, сделавшейся для меня жизненным правилом: ни один волос с головы не упадет без Его воли. А воля Его руководствуется только одною беспредельною любовью к нам, и потому всё, что ни случается с нами, всё для нашего блага. Вы спрашиваете, проведем ли мы следующую зиму в Москве? Несмотря на всё желание вас видеть, не думаю и не желаю этого. И вы удивитесь, что причиною тому Буонапарте. И вот почему: здоровье отца моего заметно слабеет: он не может переносить противоречий и делается раздражителен. Раздражительность эта, как вы знаете, обращена преимущественно на политические дела. Он не может перенести мысли о том, что Буонапарте ведет дело как с равными, со всеми государями Европы и в особенности с нашим, внуком Великой Екатерины! Как вы знаете, я совершенно равнодушна к политическим делам, но из слов моего отца и разговоров его с Михаилом Ивановичем, я знаю всё, что делается в мире, и в особенности все почести, воздаваемые Буонапарте, которого, как кажется, еще только в Лысых Горах на всем земном шаре не признают ни великим человеком, ни еще менее французским императором. И мой отец не может переносить этого. Мне кажется, что мой отец, преимущественно вследствие своего взгляда на политические дела и предвидя столкновения, которые у него будут, вследствие его манеры, не стесняясь ни с кем, высказывать свои мнения, неохотно говорит о поездке в Москву. Всё, что он выиграет от лечения, он потеряет вследствие споров о Буонапарте, которые неминуемы. Во всяком случае это решится очень скоро. Семейная жизнь наша идет по старому, за исключением присутствия брата Андрея. Он, как я уже писала вам, очень изменился последнее время. После его горя, он теперь только, в нынешнем году, совершенно нравственно ожил. Он стал таким, каким я его знала ребенком: добрым, нежным, с тем золотым сердцем, которому я не знаю равного. Он понял, как мне кажется, что жизнь для него не кончена. Но вместе с этой нравственной переменой, он физически очень ослабел. Он стал худее чем прежде, нервнее. Я боюсь за него и рада, что он предпринял эту поездку за границу, которую доктора уже давно предписывали ему. Я надеюсь, что это поправит его. Вы мне пишете, что в Петербурге о нем говорят, как об одном из самых деятельных, образованных и умных молодых людей. Простите за самолюбие родства – я никогда в этом не сомневалась. Нельзя счесть добро, которое он здесь сделал всем, начиная с своих мужиков и до дворян. Приехав в Петербург, он взял только то, что ему следовало. Удивляюсь, каким образом вообще доходят слухи из Петербурга в Москву и особенно такие неверные, как тот, о котором вы мне пишете, – слух о мнимой женитьбе брата на маленькой Ростовой. Я не думаю, чтобы Андрей когда нибудь женился на ком бы то ни было и в особенности на ней. И вот почему: во первых я знаю, что хотя он и редко говорит о покойной жене, но печаль этой потери слишком глубоко вкоренилась в его сердце, чтобы когда нибудь он решился дать ей преемницу и мачеху нашему маленькому ангелу. Во вторых потому, что, сколько я знаю, эта девушка не из того разряда женщин, которые могут нравиться князю Андрею. Не думаю, чтобы князь Андрей выбрал ее своею женою, и откровенно скажу: я не желаю этого. Но я заболталась, кончаю свой второй листок. Прощайте, мой милый друг; да сохранит вас Бог под Своим святым и могучим покровом. Моя милая подруга, mademoiselle Bourienne, целует вас.
Мари».
В середине лета, княжна Марья получила неожиданное письмо от князя Андрея из Швейцарии, в котором он сообщал ей странную и неожиданную новость. Князь Андрей объявлял о своей помолвке с Ростовой. Всё письмо его дышало любовной восторженностью к своей невесте и нежной дружбой и доверием к сестре. Он писал, что никогда не любил так, как любит теперь, и что теперь только понял и узнал жизнь; он просил сестру простить его за то, что в свой приезд в Лысые Горы он ничего не сказал ей об этом решении, хотя и говорил об этом с отцом. Он не сказал ей этого потому, что княжна Марья стала бы просить отца дать свое согласие, и не достигнув бы цели, раздражила бы отца, и на себе бы понесла всю тяжесть его неудовольствия. Впрочем, писал он, тогда еще дело не было так окончательно решено, как теперь. «Тогда отец назначил мне срок, год, и вот уже шесть месяцев, половина прошло из назначенного срока, и я остаюсь более, чем когда нибудь тверд в своем решении. Ежели бы доктора не задерживали меня здесь, на водах, я бы сам был в России, но теперь возвращение мое я должен отложить еще на три месяца. Ты знаешь меня и мои отношения с отцом. Мне ничего от него не нужно, я был и буду всегда независим, но сделать противное его воле, заслужить его гнев, когда может быть так недолго осталось ему быть с нами, разрушило бы наполовину мое счастие. Я пишу теперь ему письмо о том же и прошу тебя, выбрав добрую минуту, передать ему письмо и известить меня о том, как он смотрит на всё это и есть ли надежда на то, чтобы он согласился сократить срок на три месяца».
После долгих колебаний, сомнений и молитв, княжна Марья передала письмо отцу. На другой день старый князь сказал ей спокойно:
– Напиши брату, чтоб подождал, пока умру… Не долго – скоро развяжу…
Княжна хотела возразить что то, но отец не допустил ее, и стал всё более и более возвышать голос.
– Женись, женись, голубчик… Родство хорошее!… Умные люди, а? Богатые, а? Да. Хороша мачеха у Николушки будет! Напиши ты ему, что пускай женится хоть завтра. Мачеха Николушки будет – она, а я на Бурьенке женюсь!… Ха, ха, ха, и ему чтоб без мачехи не быть! Только одно, в моем доме больше баб не нужно; пускай женится, сам по себе живет. Может, и ты к нему переедешь? – обратился он к княжне Марье: – с Богом, по морозцу, по морозцу… по морозцу!…
После этой вспышки, князь не говорил больше ни разу об этом деле. Но сдержанная досада за малодушие сына выразилась в отношениях отца с дочерью. К прежним предлогам насмешек прибавился еще новый – разговор о мачехе и любезности к m lle Bourienne.
– Отчего же мне на ней не жениться? – говорил он дочери. – Славная княгиня будет! – И в последнее время, к недоуменью и удивлению своему, княжна Марья стала замечать, что отец ее действительно начинал больше и больше приближать к себе француженку. Княжна Марья написала князю Андрею о том, как отец принял его письмо; но утешала брата, подавая надежду примирить отца с этою мыслью.
Николушка и его воспитание, Andre и религия были утешениями и радостями княжны Марьи; но кроме того, так как каждому человеку нужны свои личные надежды, у княжны Марьи была в самой глубокой тайне ее души скрытая мечта и надежда, доставлявшая ей главное утешение в ее жизни. Утешительную эту мечту и надежду дали ей божьи люди – юродивые и странники, посещавшие ее тайно от князя. Чем больше жила княжна Марья, чем больше испытывала она жизнь и наблюдала ее, тем более удивляла ее близорукость людей, ищущих здесь на земле наслаждений и счастия; трудящихся, страдающих, борющихся и делающих зло друг другу, для достижения этого невозможного, призрачного и порочного счастия. «Князь Андрей любил жену, она умерла, ему мало этого, он хочет связать свое счастие с другой женщиной. Отец не хочет этого, потому что желает для Андрея более знатного и богатого супружества. И все они борются и страдают, и мучают, и портят свою душу, свою вечную душу, для достижения благ, которым срок есть мгновенье. Мало того, что мы сами знаем это, – Христос, сын Бога сошел на землю и сказал нам, что эта жизнь есть мгновенная жизнь, испытание, а мы всё держимся за нее и думаем в ней найти счастье. Как никто не понял этого? – думала княжна Марья. Никто кроме этих презренных божьих людей, которые с сумками за плечами приходят ко мне с заднего крыльца, боясь попасться на глаза князю, и не для того, чтобы не пострадать от него, а для того, чтобы его не ввести в грех. Оставить семью, родину, все заботы о мирских благах для того, чтобы не прилепляясь ни к чему, ходить в посконном рубище, под чужим именем с места на место, не делая вреда людям, и молясь за них, молясь и за тех, которые гонят, и за тех, которые покровительствуют: выше этой истины и жизни нет истины и жизни!»
Была одна странница, Федосьюшка, 50 ти летняя, маленькая, тихенькая, рябая женщина, ходившая уже более 30 ти лет босиком и в веригах. Ее особенно любила княжна Марья. Однажды, когда в темной комнате, при свете одной лампадки, Федосьюшка рассказывала о своей жизни, – княжне Марье вдруг с такой силой пришла мысль о том, что Федосьюшка одна нашла верный путь жизни, что она решилась сама пойти странствовать. Когда Федосьюшка пошла спать, княжна Марья долго думала над этим и наконец решила, что как ни странно это было – ей надо было итти странствовать. Она поверила свое намерение только одному духовнику монаху, отцу Акинфию, и духовник одобрил ее намерение. Под предлогом подарка странницам, княжна Марья припасла себе полное одеяние странницы: рубашку, лапти, кафтан и черный платок. Часто подходя к заветному комоду, княжна Марья останавливалась в нерешительности о том, не наступило ли уже время для приведения в исполнение ее намерения.
Часто слушая рассказы странниц, она возбуждалась их простыми, для них механическими, а для нее полными глубокого смысла речами, так что она была несколько раз готова бросить всё и бежать из дому. В воображении своем она уже видела себя с Федосьюшкой в грубом рубище, шагающей с палочкой и котомочкой по пыльной дороге, направляя свое странствие без зависти, без любви человеческой, без желаний от угодников к угодникам, и в конце концов, туда, где нет ни печали, ни воздыхания, а вечная радость и блаженство.
«Приду к одному месту, помолюсь; не успею привыкнуть, полюбить – пойду дальше. И буду итти до тех пор, пока ноги подкосятся, и лягу и умру где нибудь, и приду наконец в ту вечную, тихую пристань, где нет ни печали, ни воздыхания!…» думала княжна Марья.
Но потом, увидав отца и особенно маленького Коко, она ослабевала в своем намерении, потихоньку плакала и чувствовала, что она грешница: любила отца и племянника больше, чем Бога.
Библейское предание говорит, что отсутствие труда – праздность была условием блаженства первого человека до его падения. Любовь к праздности осталась та же и в падшем человеке, но проклятие всё тяготеет над человеком, и не только потому, что мы в поте лица должны снискивать хлеб свой, но потому, что по нравственным свойствам своим мы не можем быть праздны и спокойны. Тайный голос говорит, что мы должны быть виновны за то, что праздны. Ежели бы мог человек найти состояние, в котором он, будучи праздным, чувствовал бы себя полезным и исполняющим свой долг, он бы нашел одну сторону первобытного блаженства. И таким состоянием обязательной и безупречной праздности пользуется целое сословие – сословие военное. В этой то обязательной и безупречной праздности состояла и будет состоять главная привлекательность военной службы.
Николай Ростов испытывал вполне это блаженство, после 1807 года продолжая служить в Павлоградском полку, в котором он уже командовал эскадроном, принятым от Денисова.
Ростов сделался загрубелым, добрым малым, которого московские знакомые нашли бы несколько mauvais genre [дурного тона], но который был любим и уважаем товарищами, подчиненными и начальством и который был доволен своей жизнью. В последнее время, в 1809 году, он чаще в письмах из дому находил сетования матери на то, что дела расстраиваются хуже и хуже, и что пора бы ему приехать домой, обрадовать и успокоить стариков родителей.
Читая эти письма, Николай испытывал страх, что хотят вывести его из той среды, в которой он, оградив себя от всей житейской путаницы, жил так тихо и спокойно. Он чувствовал, что рано или поздно придется опять вступить в тот омут жизни с расстройствами и поправлениями дел, с учетами управляющих, ссорами, интригами, с связями, с обществом, с любовью Сони и обещанием ей. Всё это было страшно трудно, запутано, и он отвечал на письма матери, холодными классическими письмами, начинавшимися: Ma chere maman [Моя милая матушка] и кончавшимися: votre obeissant fils, [Ваш послушный сын,] умалчивая о том, когда он намерен приехать. В 1810 году он получил письма родных, в которых извещали его о помолвке Наташи с Болконским и о том, что свадьба будет через год, потому что старый князь не согласен. Это письмо огорчило, оскорбило Николая. Во первых, ему жалко было потерять из дома Наташу, которую он любил больше всех из семьи; во вторых, он с своей гусарской точки зрения жалел о том, что его не было при этом, потому что он бы показал этому Болконскому, что совсем не такая большая честь родство с ним и что, ежели он любит Наташу, то может обойтись и без разрешения сумасбродного отца. Минуту он колебался не попроситься ли в отпуск, чтоб увидать Наташу невестой, но тут подошли маневры, пришли соображения о Соне, о путанице, и Николай опять отложил. Но весной того же года он получил письмо матери, писавшей тайно от графа, и письмо это убедило его ехать. Она писала, что ежели Николай не приедет и не возьмется за дела, то всё именье пойдет с молотка и все пойдут по миру. Граф так слаб, так вверился Митеньке, и так добр, и так все его обманывают, что всё идет хуже и хуже. «Ради Бога, умоляю тебя, приезжай сейчас же, ежели ты не хочешь сделать меня и всё твое семейство несчастными», писала графиня.
Письмо это подействовало на Николая. У него был тот здравый смысл посредственности, который показывал ему, что было должно.
Теперь должно было ехать, если не в отставку, то в отпуск. Почему надо было ехать, он не знал; но выспавшись после обеда, он велел оседлать серого Марса, давно не езженного и страшно злого жеребца, и вернувшись на взмыленном жеребце домой, объявил Лаврушке (лакей Денисова остался у Ростова) и пришедшим вечером товарищам, что подает в отпуск и едет домой. Как ни трудно и странно было ему думать, что он уедет и не узнает из штаба (что ему особенно интересно было), произведен ли он будет в ротмистры, или получит Анну за последние маневры; как ни странно было думать, что он так и уедет, не продав графу Голуховскому тройку саврасых, которых польский граф торговал у него, и которых Ростов на пари бил, что продаст за 2 тысячи, как ни непонятно казалось, что без него будет тот бал, который гусары должны были дать панне Пшаздецкой в пику уланам, дававшим бал своей панне Боржозовской, – он знал, что надо ехать из этого ясного, хорошего мира куда то туда, где всё было вздор и путаница.
Через неделю вышел отпуск. Гусары товарищи не только по полку, но и по бригаде, дали обед Ростову, стоивший с головы по 15 руб. подписки, – играли две музыки, пели два хора песенников; Ростов плясал трепака с майором Басовым; пьяные офицеры качали, обнимали и уронили Ростова; солдаты третьего эскадрона еще раз качали его, и кричали ура! Потом Ростова положили в сани и проводили до первой станции.
До половины дороги, как это всегда бывает, от Кременчуга до Киева, все мысли Ростова были еще назади – в эскадроне; но перевалившись за половину, он уже начал забывать тройку саврасых, своего вахмистра Дожойвейку, и беспокойно начал спрашивать себя о том, что и как он найдет в Отрадном. Чем ближе он подъезжал, тем сильнее, гораздо сильнее (как будто нравственное чувство было подчинено тому же закону скорости падения тел в квадратах расстояний), он думал о своем доме; на последней перед Отрадным станции, дал ямщику три рубля на водку, и как мальчик задыхаясь вбежал на крыльцо дома.
После восторгов встречи, и после того странного чувства неудовлетворения в сравнении с тем, чего ожидаешь – всё то же, к чему же я так торопился! – Николай стал вживаться в свой старый мир дома. Отец и мать были те же, они только немного постарели. Новое в них било какое то беспокойство и иногда несогласие, которого не бывало прежде и которое, как скоро узнал Николай, происходило от дурного положения дел. Соне был уже двадцатый год. Она уже остановилась хорошеть, ничего не обещала больше того, что в ней было; но и этого было достаточно. Она вся дышала счастьем и любовью с тех пор как приехал Николай, и верная, непоколебимая любовь этой девушки радостно действовала на него. Петя и Наташа больше всех удивили Николая. Петя был уже большой, тринадцатилетний, красивый, весело и умно шаловливый мальчик, у которого уже ломался голос. На Наташу Николай долго удивлялся, и смеялся, глядя на нее.
– Совсем не та, – говорил он.
– Что ж, подурнела?
– Напротив, но важность какая то. Княгиня! – сказал он ей шопотом.
– Да, да, да, – радостно говорила Наташа.
Наташа рассказала ему свой роман с князем Андреем, его приезд в Отрадное и показала его последнее письмо.
– Что ж ты рад? – спрашивала Наташа. – Я так теперь спокойна, счастлива.
– Очень рад, – отвечал Николай. – Он отличный человек. Что ж ты очень влюблена?
– Как тебе сказать, – отвечала Наташа, – я была влюблена в Бориса, в учителя, в Денисова, но это совсем не то. Мне покойно, твердо. Я знаю, что лучше его не бывает людей, и мне так спокойно, хорошо теперь. Совсем не так, как прежде…
Николай выразил Наташе свое неудовольствие о том, что свадьба была отложена на год; но Наташа с ожесточением напустилась на брата, доказывая ему, что это не могло быть иначе, что дурно бы было вступить в семью против воли отца, что она сама этого хотела.
– Ты совсем, совсем не понимаешь, – говорила она. Николай замолчал и согласился с нею.
Брат часто удивлялся глядя на нее. Совсем не было похоже, чтобы она была влюбленная невеста в разлуке с своим женихом. Она была ровна, спокойна, весела совершенно по прежнему. Николая это удивляло и даже заставляло недоверчиво смотреть на сватовство Болконского. Он не верил в то, что ее судьба уже решена, тем более, что он не видал с нею князя Андрея. Ему всё казалось, что что нибудь не то, в этом предполагаемом браке.
«Зачем отсрочка? Зачем не обручились?» думал он. Разговорившись раз с матерью о сестре, он, к удивлению своему и отчасти к удовольствию, нашел, что мать точно так же в глубине души иногда недоверчиво смотрела на этот брак.
– Вот пишет, – говорила она, показывая сыну письмо князя Андрея с тем затаенным чувством недоброжелательства, которое всегда есть у матери против будущего супружеского счастия дочери, – пишет, что не приедет раньше декабря. Какое же это дело может задержать его? Верно болезнь! Здоровье слабое очень. Ты не говори Наташе. Ты не смотри, что она весела: это уж последнее девичье время доживает, а я знаю, что с ней делается всякий раз, как письма его получаем. А впрочем Бог даст, всё и хорошо будет, – заключала она всякий раз: – он отличный человек.
Первое время своего приезда Николай был серьезен и даже скучен. Его мучила предстоящая необходимость вмешаться в эти глупые дела хозяйства, для которых мать вызвала его. Чтобы скорее свалить с плеч эту обузу, на третий день своего приезда он сердито, не отвечая на вопрос, куда он идет, пошел с нахмуренными бровями во флигель к Митеньке и потребовал у него счеты всего. Что такое были эти счеты всего, Николай знал еще менее, чем пришедший в страх и недоумение Митенька. Разговор и учет Митеньки продолжался недолго. Староста, выборный и земский, дожидавшиеся в передней флигеля, со страхом и удовольствием слышали сначала, как загудел и затрещал как будто всё возвышавшийся голос молодого графа, слышали ругательные и страшные слова, сыпавшиеся одно за другим.
– Разбойник! Неблагодарная тварь!… изрублю собаку… не с папенькой… обворовал… – и т. д.
Потом эти люди с неменьшим удовольствием и страхом видели, как молодой граф, весь красный, с налитой кровью в глазах, за шиворот вытащил Митеньку, ногой и коленкой с большой ловкостью в удобное время между своих слов толкнул его под зад и закричал: «Вон! чтобы духу твоего, мерзавец, здесь не было!»
Митенька стремглав слетел с шести ступеней и убежал в клумбу. (Клумба эта была известная местность спасения преступников в Отрадном. Сам Митенька, приезжая пьяный из города, прятался в эту клумбу, и многие жители Отрадного, прятавшиеся от Митеньки, знали спасительную силу этой клумбы.)
Жена Митеньки и свояченицы с испуганными лицами высунулись в сени из дверей комнаты, где кипел чистый самовар и возвышалась приказчицкая высокая постель под стеганным одеялом, сшитым из коротких кусочков.
Молодой граф, задыхаясь, не обращая на них внимания, решительными шагами прошел мимо них и пошел в дом.
Графиня узнавшая тотчас через девушек о том, что произошло во флигеле, с одной стороны успокоилась в том отношении, что теперь состояние их должно поправиться, с другой стороны она беспокоилась о том, как перенесет это ее сын. Она подходила несколько раз на цыпочках к его двери, слушая, как он курил трубку за трубкой.
На другой день старый граф отозвал в сторону сына и с робкой улыбкой сказал ему:
– А знаешь ли, ты, моя душа, напрасно погорячился! Мне Митенька рассказал все.
«Я знал, подумал Николай, что никогда ничего не пойму здесь, в этом дурацком мире».
– Ты рассердился, что он не вписал эти 700 рублей. Ведь они у него написаны транспортом, а другую страницу ты не посмотрел.
– Папенька, он мерзавец и вор, я знаю. И что сделал, то сделал. А ежели вы не хотите, я ничего не буду говорить ему.
– Нет, моя душа (граф был смущен тоже. Он чувствовал, что он был дурным распорядителем имения своей жены и виноват был перед своими детьми но не знал, как поправить это) – Нет, я прошу тебя заняться делами, я стар, я…
– Нет, папенька, вы простите меня, ежели я сделал вам неприятное; я меньше вашего умею.
«Чорт с ними, с этими мужиками и деньгами, и транспортами по странице, думал он. Еще от угла на шесть кушей я понимал когда то, но по странице транспорт – ничего не понимаю», сказал он сам себе и с тех пор более не вступался в дела. Только однажды графиня позвала к себе сына, сообщила ему о том, что у нее есть вексель Анны Михайловны на две тысячи и спросила у Николая, как он думает поступить с ним.
– А вот как, – отвечал Николай. – Вы мне сказали, что это от меня зависит; я не люблю Анну Михайловну и не люблю Бориса, но они были дружны с нами и бедны. Так вот как! – и он разорвал вексель, и этим поступком слезами радости заставил рыдать старую графиню. После этого молодой Ростов, уже не вступаясь более ни в какие дела, с страстным увлечением занялся еще новыми для него делами псовой охоты, которая в больших размерах была заведена у старого графа.
Уже были зазимки, утренние морозы заковывали смоченную осенними дождями землю, уже зелень уклочилась и ярко зелено отделялась от полос буреющего, выбитого скотом, озимого и светло желтого ярового жнивья с красными полосами гречихи. Вершины и леса, в конце августа еще бывшие зелеными островами между черными полями озимей и жнивами, стали золотистыми и ярко красными островами посреди ярко зеленых озимей. Русак уже до половины затерся (перелинял), лисьи выводки начинали разбредаться, и молодые волки были больше собаки. Было лучшее охотничье время. Собаки горячего, молодого охотника Ростова уже не только вошли в охотничье тело, но и подбились так, что в общем совете охотников решено было три дня дать отдохнуть собакам и 16 сентября итти в отъезд, начиная с дубравы, где был нетронутый волчий выводок.
В таком положении были дела 14 го сентября.
Весь этот день охота была дома; было морозно и колко, но с вечера стало замолаживать и оттеплело. 15 сентября, когда молодой Ростов утром в халате выглянул в окно, он увидал такое утро, лучше которого ничего не могло быть для охоты: как будто небо таяло и без ветра спускалось на землю. Единственное движенье, которое было в воздухе, было тихое движенье сверху вниз спускающихся микроскопических капель мги или тумана. На оголившихся ветвях сада висели прозрачные капли и падали на только что свалившиеся листья. Земля на огороде, как мак, глянцевито мокро чернела, и в недалеком расстоянии сливалась с тусклым и влажным покровом тумана. Николай вышел на мокрое с натасканной грязью крыльцо: пахло вянущим лесом и собаками. Чернопегая, широкозадая сука Милка с большими черными на выкате глазами, увидав хозяина, встала, потянулась назад и легла по русачьи, потом неожиданно вскочила и лизнула его прямо в нос и усы. Другая борзая собака, увидав хозяина с цветной дорожки, выгибая спину, стремительно бросилась к крыльцу и подняв правило (хвост), стала тереться о ноги Николая.
– О гой! – послышался в это время тот неподражаемый охотничий подклик, который соединяет в себе и самый глубокий бас, и самый тонкий тенор; и из за угла вышел доезжачий и ловчий Данило, по украински в скобку обстриженный, седой, морщинистый охотник с гнутым арапником в руке и с тем выражением самостоятельности и презрения ко всему в мире, которое бывает только у охотников. Он снял свою черкесскую шапку перед барином, и презрительно посмотрел на него. Презрение это не было оскорбительно для барина: Николай знал, что этот всё презирающий и превыше всего стоящий Данило всё таки был его человек и охотник.
– Данила! – сказал Николай, робко чувствуя, что при виде этой охотничьей погоды, этих собак и охотника, его уже обхватило то непреодолимое охотничье чувство, в котором человек забывает все прежние намерения, как человек влюбленный в присутствии своей любовницы.
– Что прикажете, ваше сиятельство? – спросил протодиаконский, охриплый от порсканья бас, и два черные блестящие глаза взглянули исподлобья на замолчавшего барина. «Что, или не выдержишь?» как будто сказали эти два глаза.
– Хорош денек, а? И гоньба, и скачка, а? – сказал Николай, чеша за ушами Милку.
Данило не отвечал и помигал глазами.
– Уварку посылал послушать на заре, – сказал его бас после минутного молчанья, – сказывал, в отрадненский заказ перевела, там выли. (Перевела значило то, что волчица, про которую они оба знали, перешла с детьми в отрадненский лес, который был за две версты от дома и который был небольшое отъемное место.)
– А ведь ехать надо? – сказал Николай. – Приди ка ко мне с Уваркой.
– Как прикажете!
– Так погоди же кормить.
– Слушаю.
Через пять минут Данило с Уваркой стояли в большом кабинете Николая. Несмотря на то, что Данило был не велик ростом, видеть его в комнате производило впечатление подобное тому, как когда видишь лошадь или медведя на полу между мебелью и условиями людской жизни. Данило сам это чувствовал и, как обыкновенно, стоял у самой двери, стараясь говорить тише, не двигаться, чтобы не поломать как нибудь господских покоев, и стараясь поскорее всё высказать и выйти на простор, из под потолка под небо.
Окончив расспросы и выпытав сознание Данилы, что собаки ничего (Даниле и самому хотелось ехать), Николай велел седлать. Но только что Данила хотел выйти, как в комнату вошла быстрыми шагами Наташа, еще не причесанная и не одетая, в большом, нянином платке. Петя вбежал вместе с ней.
– Ты едешь? – сказала Наташа, – я так и знала! Соня говорила, что не поедете. Я знала, что нынче такой день, что нельзя не ехать.
– Едем, – неохотно отвечал Николай, которому нынче, так как он намеревался предпринять серьезную охоту, не хотелось брать Наташу и Петю. – Едем, да только за волками: тебе скучно будет.
– Ты знаешь, что это самое большое мое удовольствие, – сказала Наташа.
– Это дурно, – сам едет, велел седлать, а нам ничего не сказал.
– Тщетны россам все препоны, едем! – прокричал Петя.
– Да ведь тебе и нельзя: маменька сказала, что тебе нельзя, – сказал Николай, обращаясь к Наташе.
– Нет, я поеду, непременно поеду, – сказала решительно Наташа. – Данила, вели нам седлать, и Михайла чтоб выезжал с моей сворой, – обратилась она к ловчему.
И так то быть в комнате Даниле казалось неприлично и тяжело, но иметь какое нибудь дело с барышней – для него казалось невозможным. Он опустил глаза и поспешил выйти, как будто до него это не касалось, стараясь как нибудь нечаянно не повредить барышне.

