Конус

|
конус в Викисловаре? |
|---|
Конус (от др.-греч. κώνος «сосновая шишка»[1]) — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Если основание конуса представляет собой многоугольник, такой конус является пирамидой.
Содержание
Связанные определения
- Отрезок, соединяющий вершину и границу основания, называется образующей конуса.
- Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью.
- Отрезок, опущенный перпендикулярно из вершины на плоскость основания (а также длина такого отрезка), называется высотой конуса.
- Угол раствора конуса — угол между двумя противоположными образующими (угол при вершине конуса, внутри конуса).
- Если основание конуса имеет центр симметрии (например, является кругом или эллипсом) и ортогональная проекция вершины конуса на плоскость основания совпадает с этим центром, то конус называется прямым. При этом прямая, соединяющая вершину и центр основания, называется осью конуса.
- Косой (наклонный) конус — конус, у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии.
- Круговой конус — конус, основание которого является кругом.
- Прямой круговой конус (часто его называют просто конусом) можно получить вращением прямоугольного треугольника вокруг прямой, содержащей катет (эта прямая представляет собой ось конуса).
- Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом (последние два имеют бесконечный объём).
- Часть конуса, лежащая между основанием и плоскостью, параллельной основанию и находящейся между вершиной и основанием, называется усечённым конусом, или коническим слоем.
Свойства
- Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.
- <math>V={1 \over 3} SH,</math>
где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.
- Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.
- Телесный угол при вершине прямого кругового конуса равен
- <math>2\pi \left(1 - \cos {\alpha \over 2} \right),</math>
- где α — угол раствора конуса.
- Площадь боковой поверхности такого конуса равна
- <math>S = \pi R l,</math>
а полная площадь поверхности (т. е. сумма площадей боковой поверхности и основания)
- <math>S = \pi R (l + R),</math>
- где R — радиус основания, l — длина образующей.
- Объём кругового конуса равен
- <math>V={1 \over 3} \pi R^2H.</math>
- Для усечённого конуса (не обязательно прямого и кругового) объём равен:
- <math>V={1 \over 3} (HS_2-hS_1),</math>
где S1 и S2 — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.
- Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).
Уравнение конуса
Уравнения, задающие боковую поверхность прямого кругового конуса с углом раствора 2Θ, вершиной в начале координат и осью, совпадающей с осью Oz:
- В сферической системе координат с координатами (r, φ, θ):
- <math>\theta = \Theta.</math>
- В цилиндрической системе координат с координатами (r, φ, z):
- <math>z = r\cdot\operatorname{ctg}\Theta</math> или <math>r = z\cdot\operatorname{tg}\Theta.</math>
- В декартовой системе координат с координатами (x, y, z):
- <math>z = \plusmn \sqrt{x^2+y^2}\cdot \operatorname{ctg}\Theta.</math> Это уравнение в каноническом виде записывается как
- <math>\frac {x^2} {a^2} + \frac {y^2} {b^2} - \frac {z^2} {c^2} = 0,</math>
где константы a, с определяются пропорцией <math>c/a = \cos \Theta/\sin\Theta.</math> Отсюда видно, что боковая поверхность прямого кругового конуса представляет собой поверхность второго порядка (она носит название коническая поверхность). В общем виде коническая поверхность второго порядка опирается на эллипс; в подходящей декартовой координатной системе (оси Ох и Оу параллельны осям эллипса, вершина конуса совпадает с началом координат, центр эллипса лежит на оси Oz) её уравнение имеет вид
- <math>\frac {x^2} {a^2} + \frac {y^2} {b^2} - \frac {z^2} {c^2} = 0,</math>
причём a/c и b/c равны полуосям эллипса. В наиболее общем случае, когда конус опирается на произвольную плоскую поверхность, можно показать, что уравнение боковой поверхности конуса (с вершиной в начале координат) задаётся уравнением <math>f(x,y,z)=0,</math> где функция <math>f(x,y,z)</math> является однородной, то есть удовлетворяющей условию <math>f(\alpha x,\alpha y,\alpha z)=\alpha^n f(x,y,z)</math> для любого действительного числа α.
Развёртка
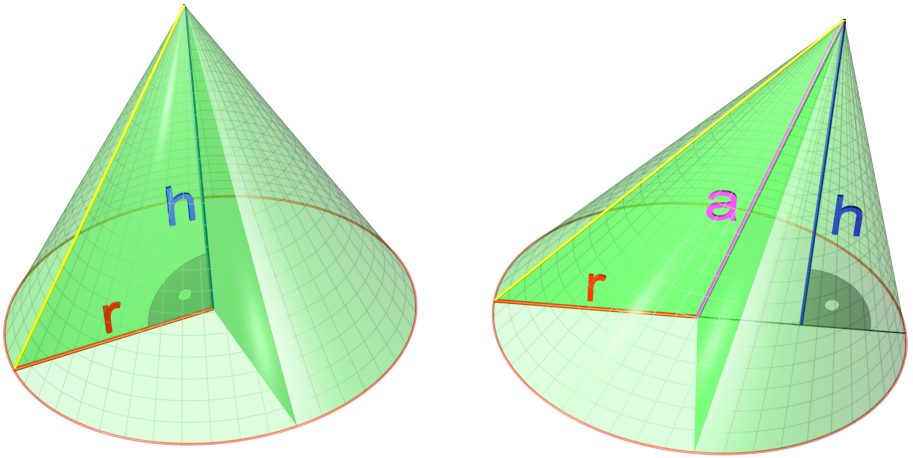
 Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.
Прямой круговой конус как тело вращения образован прямоугольным треугольником, вращающимся вокруг одного из катетов, где h — высота конуса от центра основания до вершины — является катетом прямоугольного треугольника, вокруг которого происходит вращение. Второй катет прямоугольного треугольника r — радиус в основании конуса. Гипотенузой прямоугольного треугольника является l — образующая конуса.
В создании развёртки конуса могут использоваться всего две величины r и l. Радиус основания r определяет в развертке круг основания конуса, а сектор боковой поверхности конуса определяет образующая боковой поверхности l, являющаяся радиусом сектора боковой поверхности. Угол сектора <math>\varphi</math> в развёртке боковой поверхности конуса определяется по формуле:
- φ = 360°·(r/l).
Вариации и обобщения
- В алгебраической геометрии конус — это произвольное подмножество <math>K</math> векторного пространства <math>V</math> над полем <math>F</math>, для которого для любого <math>\lambda\in F</math>
- <math>\lambda K = K.</math>
- В топологии конус над топологическим пространством X есть фактор-пространство <math>X\times [0,\infty)</math> по отношению эквивалентности (<math>x,0)\sim (y,0).</math>
См. также
- Коническая поверхность
- Коническое сечение
- Конус (топология)
- Световой конус
- Конус отображения
- Биконус
Напишите отзыв о статье "Конус"
Примечания
- ↑ [lingvowiki.info/w/Книги/Древнегреческо-русский_словарь_Дворецкого/76 Древнегреческо-русский словарь Дворецкого «I κῶνος»]
Литература
- Статья [dic.academic.ru/dic.nsf/enc_mathematics/2403/%D0%9A%D0%9E%D0%9D%D0%A3%D0%A1 «Конус»] в Математической энциклопедии.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1973.
Отрывок, характеризующий Конус
Князь Андрей приехал в квартиру генерала Бенигсена, занимавшего небольшой помещичий дом на самом берегу реки. Ни Бенигсена, ни государя не было там, но Чернышев, флигель адъютант государя, принял Болконского и объявил ему, что государь поехал с генералом Бенигсеном и с маркизом Паулучи другой раз в нынешний день для объезда укреплений Дрисского лагеря, в удобности которого начинали сильно сомневаться.Чернышев сидел с книгой французского романа у окна первой комнаты. Комната эта, вероятно, была прежде залой; в ней еще стоял орган, на который навалены были какие то ковры, и в одном углу стояла складная кровать адъютанта Бенигсена. Этот адъютант был тут. Он, видно, замученный пирушкой или делом, сидел на свернутой постеле и дремал. Из залы вели две двери: одна прямо в бывшую гостиную, другая направо в кабинет. Из первой двери слышались голоса разговаривающих по немецки и изредка по французски. Там, в бывшей гостиной, были собраны, по желанию государя, не военный совет (государь любил неопределенность), но некоторые лица, которых мнение о предстоящих затруднениях он желал знать. Это не был военный совет, но как бы совет избранных для уяснения некоторых вопросов лично для государя. На этот полусовет были приглашены: шведский генерал Армфельд, генерал адъютант Вольцоген, Винцингероде, которого Наполеон называл беглым французским подданным, Мишо, Толь, вовсе не военный человек – граф Штейн и, наконец, сам Пфуль, который, как слышал князь Андрей, был la cheville ouvriere [основою] всего дела. Князь Андрей имел случай хорошо рассмотреть его, так как Пфуль вскоре после него приехал и прошел в гостиную, остановившись на минуту поговорить с Чернышевым.
Пфуль с первого взгляда, в своем русском генеральском дурно сшитом мундире, который нескладно, как на наряженном, сидел на нем, показался князю Андрею как будто знакомым, хотя он никогда не видал его. В нем был и Вейротер, и Мак, и Шмидт, и много других немецких теоретиков генералов, которых князю Андрею удалось видеть в 1805 м году; но он был типичнее всех их. Такого немца теоретика, соединявшего в себе все, что было в тех немцах, еще никогда не видал князь Андрей.
Пфуль был невысок ростом, очень худ, но ширококост, грубого, здорового сложения, с широким тазом и костлявыми лопатками. Лицо у него было очень морщинисто, с глубоко вставленными глазами. Волоса его спереди у висков, очевидно, торопливо были приглажены щеткой, сзади наивно торчали кисточками. Он, беспокойно и сердито оглядываясь, вошел в комнату, как будто он всего боялся в большой комнате, куда он вошел. Он, неловким движением придерживая шпагу, обратился к Чернышеву, спрашивая по немецки, где государь. Ему, видно, как можно скорее хотелось пройти комнаты, окончить поклоны и приветствия и сесть за дело перед картой, где он чувствовал себя на месте. Он поспешно кивал головой на слова Чернышева и иронически улыбался, слушая его слова о том, что государь осматривает укрепления, которые он, сам Пфуль, заложил по своей теории. Он что то басисто и круто, как говорят самоуверенные немцы, проворчал про себя: Dummkopf… или: zu Grunde die ganze Geschichte… или: s'wird was gescheites d'raus werden… [глупости… к черту все дело… (нем.) ] Князь Андрей не расслышал и хотел пройти, но Чернышев познакомил князя Андрея с Пфулем, заметив, что князь Андрей приехал из Турции, где так счастливо кончена война. Пфуль чуть взглянул не столько на князя Андрея, сколько через него, и проговорил смеясь: «Da muss ein schoner taktischcr Krieg gewesen sein». [«То то, должно быть, правильно тактическая была война.» (нем.) ] – И, засмеявшись презрительно, прошел в комнату, из которой слышались голоса.
Видно, Пфуль, уже всегда готовый на ироническое раздражение, нынче был особенно возбужден тем, что осмелились без него осматривать его лагерь и судить о нем. Князь Андрей по одному короткому этому свиданию с Пфулем благодаря своим аустерлицким воспоминаниям составил себе ясную характеристику этого человека. Пфуль был один из тех безнадежно, неизменно, до мученичества самоуверенных людей, которыми только бывают немцы, и именно потому, что только немцы бывают самоуверенными на основании отвлеченной идеи – науки, то есть мнимого знания совершенной истины. Француз бывает самоуверен потому, что он почитает себя лично, как умом, так и телом, непреодолимо обворожительным как для мужчин, так и для женщин. Англичанин самоуверен на том основании, что он есть гражданин благоустроеннейшего в мире государства, и потому, как англичанин, знает всегда, что ему делать нужно, и знает, что все, что он делает как англичанин, несомненно хорошо. Итальянец самоуверен потому, что он взволнован и забывает легко и себя и других. Русский самоуверен именно потому, что он ничего не знает и знать не хочет, потому что не верит, чтобы можно было вполне знать что нибудь. Немец самоуверен хуже всех, и тверже всех, и противнее всех, потому что он воображает, что знает истину, науку, которую он сам выдумал, но которая для него есть абсолютная истина. Таков, очевидно, был Пфуль. У него была наука – теория облического движения, выведенная им из истории войн Фридриха Великого, и все, что встречалось ему в новейшей истории войн Фридриха Великого, и все, что встречалось ему в новейшей военной истории, казалось ему бессмыслицей, варварством, безобразным столкновением, в котором с обеих сторон было сделано столько ошибок, что войны эти не могли быть названы войнами: они не подходили под теорию и не могли служить предметом науки.
В 1806 м году Пфуль был одним из составителей плана войны, кончившейся Иеной и Ауерштетом; но в исходе этой войны он не видел ни малейшего доказательства неправильности своей теории. Напротив, сделанные отступления от его теории, по его понятиям, были единственной причиной всей неудачи, и он с свойственной ему радостной иронией говорил: «Ich sagte ja, daji die ganze Geschichte zum Teufel gehen wird». [Ведь я же говорил, что все дело пойдет к черту (нем.) ] Пфуль был один из тех теоретиков, которые так любят свою теорию, что забывают цель теории – приложение ее к практике; он в любви к теории ненавидел всякую практику и знать ее не хотел. Он даже радовался неуспеху, потому что неуспех, происходивший от отступления в практике от теории, доказывал ему только справедливость его теории.
Он сказал несколько слов с князем Андреем и Чернышевым о настоящей войне с выражением человека, который знает вперед, что все будет скверно и что даже не недоволен этим. Торчавшие на затылке непричесанные кисточки волос и торопливо прилизанные височки особенно красноречиво подтверждали это.
Он прошел в другую комнату, и оттуда тотчас же послышались басистые и ворчливые звуки его голоса.
Не успел князь Андрей проводить глазами Пфуля, как в комнату поспешно вошел граф Бенигсен и, кивнув головой Болконскому, не останавливаясь, прошел в кабинет, отдавая какие то приказания своему адъютанту. Государь ехал за ним, и Бенигсен поспешил вперед, чтобы приготовить кое что и успеть встретить государя. Чернышев и князь Андрей вышли на крыльцо. Государь с усталым видом слезал с лошади. Маркиз Паулучи что то говорил государю. Государь, склонив голову налево, с недовольным видом слушал Паулучи, говорившего с особенным жаром. Государь тронулся вперед, видимо, желая окончить разговор, но раскрасневшийся, взволнованный итальянец, забывая приличия, шел за ним, продолжая говорить: