Метод конечных элементов

Метод конечных элементов (МКЭ) — это численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики и электродинамики.

Идея метода

Суть метода следует из его названия. Область, в которой ищется решение дифференциальных уравнений, разбивается на конечное количество подобластей (элементов). В каждом из элементов произвольно выбирается вид аппроксимирующей функции. В простейшем случае это полином первой степени. Вне своего элемента аппроксимирующая функция равна нулю. Значения функций на границах элементов (в узлах) являются решением задачи и заранее неизвестны. Коэффициенты аппроксимирующих функций обычно ищутся из условия равенства значения соседних функций на границах между элементами (в узлах). Затем эти коэффициенты выражаются через значения функций в узлах элементов. Составляется система линейных алгебраических уравнений. Количество уравнений равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы, прямо пропорционально количеству элементов и ограничивается только возможностями ЭВМ. Так как каждый из элементов связан с ограниченным количеством соседних, система линейных алгебраических уравнений имеет разрежённый вид, что существенно упрощает её решение.

Если говорить в матричных терминах, то собираются так называемые матрицы жёсткости (или матрица Дирихле) и масс. Далее на эти матрицы накладываются граничные условия (например, при условиях Неймана в матрицах не меняется ничего, а при условиях Дирихле из матриц вычёркиваются строки и столбцы, соответствующие граничным узлам, так как в силу краевых условий значение соответствующих компонент решения известно). Затем собирается система линейных уравнений и решается одним из известных методов.

С точки зрения вычислительной математики, идея метода конечных элементов заключается в том, что минимизация функционала вариационной задачи осуществляется на совокупности функций, каждая из которых определена на своей подобласти, для численного анализа системы позволяет рассматривать его как одну из конкретных ветвей диакоптики — общего метода исследования систем путём их расчленения.

Иллюстрация метода на одномерном примере

Пусть в одномерном пространстве Р1 необходимо решить следующее одномерное дифференциальное уравнение для нахождения функции <math>u</math> на промежутке от 0 до 1. На границах области значение функции <math>u</math> равно 0:

<math>\mbox{ P1 }:\begin{cases}

u(x)=f(x) \mbox{ in } (0,1), \\ u(0)=u(1)=0, \end{cases}</math> где <math>f</math> известная функция, <math>u</math> неизвестная функция от <math>x</math>. <math>u</math> вторая производная от <math>u</math> по <math>x</math>. Решение поставленной задачи методом конечных элементов разобьём на 2 этапа:

• Переформулируем граничную задачу в так называемую слабую (вариационную) форму. На этом этапе вычислений почти не требуется.
• На втором этапе разобьём слабую форму на конечные отрезки-элементы.

После этого возникает проблема нахождения системы линейных алгебраических уравнений, решение которой аппроксимирует искомую функцию.

Если <math>u</math> есть решение, то для любой гладкой функции <math>v</math>, которая удовлетворяет граничным условиям <math>v=0</math> в точках <math>x=0</math> и <math>x=1</math>, можно записать следующее выражение:

(1) <math>\int_0^1 f(x)v(x) \, dx = \int_0^1 u(x)v(x) \, dx.</math>

С помощью интегрирования по частям преобразуем выражение (1) к следующей форме:

(2)<math>\begin{align} \int_0^1 f(x)v(x) \, dx = \int_0^1 u(x)v(x) \, dx \\

= u'(x)v(x)\bigg|_0^1-\int_0^1 u'(x)v'(x) \, dx \\
= -\int_0^1 u'(x)v'(x) \, dx = -\phi (u,v).

\end{align} </math>

Оно получено с учётом того, что <math>v(0)=v(1)=0</math>.

Разобьём область, в которой ищется решение

<math>u \in H_0^1</math> такое, что

<math>\forall v \in H_0^1, \; -\phi(u,v)=\int_{0}^{1} f(x)v(x)dx</math>

на конечные промежутки, и получим новое пространство <math> V</math> :

(3) <math>u \in V</math> такое, что

<math>\forall v \in V, \; -\phi(u,v)=\int_{0}^{1} f(x)v(x)dx</math>

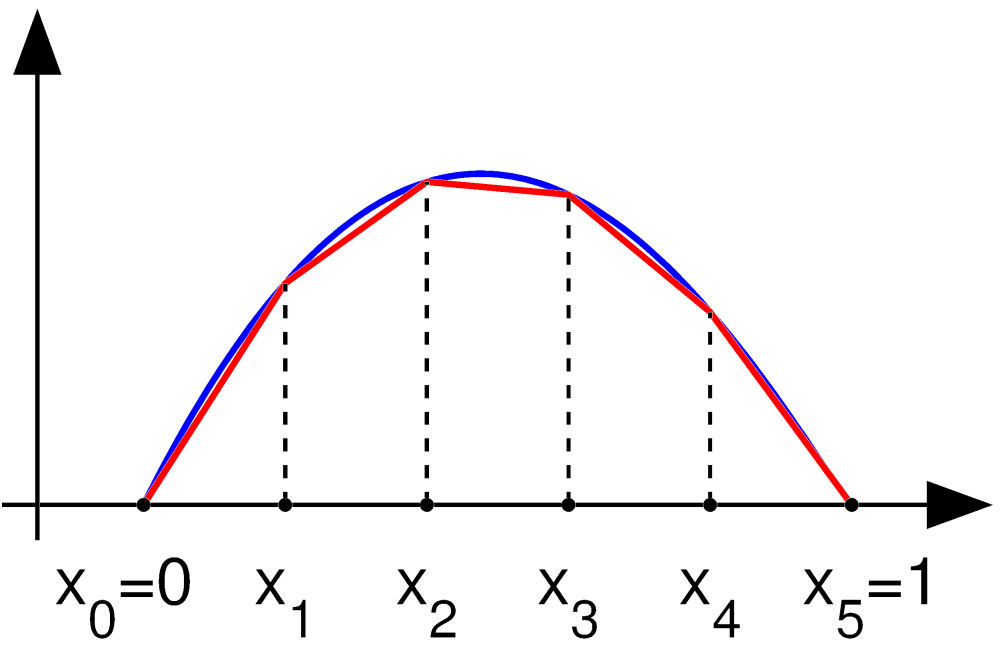
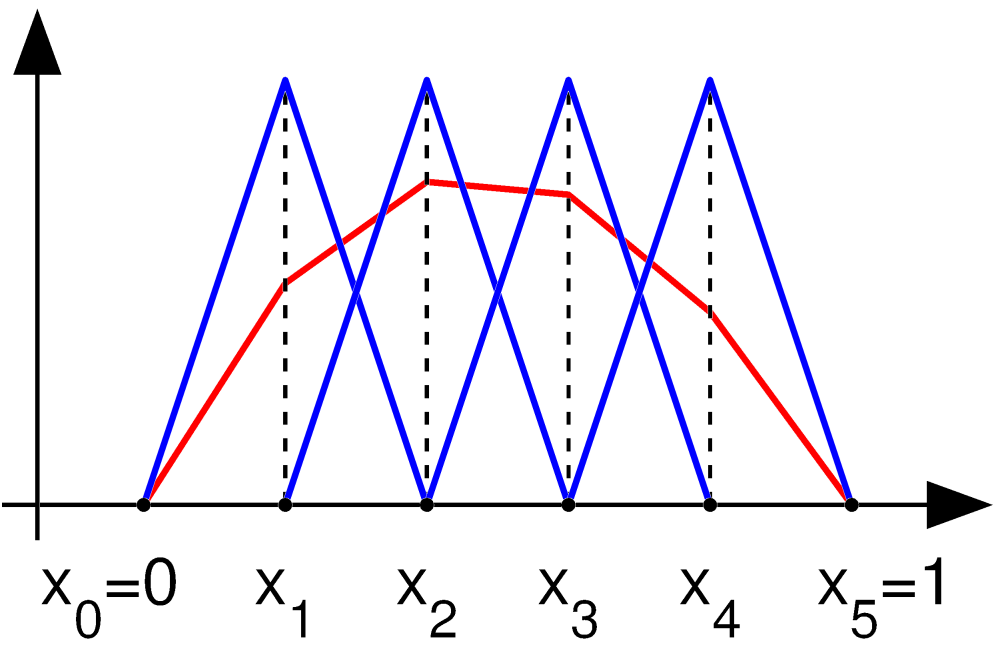
где <math>V</math> кусочная область пространства <math>H_0^1</math>. Есть много способов для выбора базиса <math>V</math>. Выберем в качестве базисных функций такие <math>v_{k}</math>, чтобы они представлялись прямыми линиями (полиномами первой степени):

<math>v_{k}(x)=\begin{cases} {x-x_{k-1} \over x_k\,-x_{k-1}} & \mbox{, } x \in [x_{k-1},x_k], \\

{x_{k+1}\,-x \over x_{k+1}\,-x_k} & \mbox{, } x \in [x_k,x_{k+1}], \\ 0 & \mbox{, } x \not\in [x_{k-1},x_{k+1}]\end{cases}</math>

для <math>k=1,\ldots,n-1</math> (в данном примере <math>n=5</math>)

Если теперь искомое приближённое решение представить виде <math>u(x)=\sum_{k=1}^{n-1} u_k v_k(x)</math>, а функцию <math>f(x)</math> аппроксимировать как <math>f(x)=\sum_{k=0}^n f_k v_k(x)</math>, то с помощью (3) можно получить следующую систему уравнений относительно искомых <math>u_k</math>:

<math>-\sum_{k=1}^{n-1} u_k \phi (v_k,v_j) = \sum_{k=0}^n f_k \int v_k v_j dx</math>,

где <math>j=1,\ldots,n-1</math>.

Преимущества и недостатки

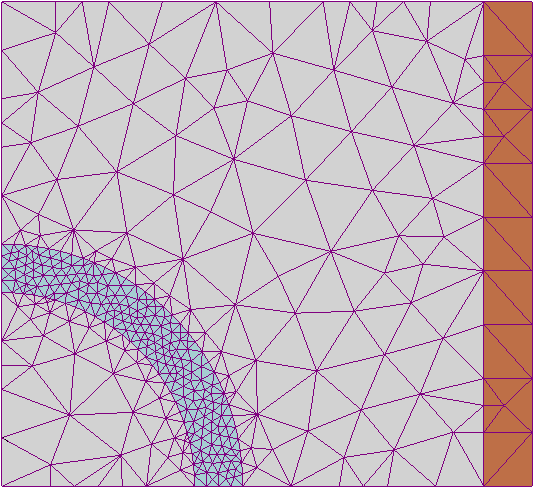
Метод конечных элементов сложнее метода конечных разностей в реализации. У МКЭ, однако, есть ряд преимуществ, проявляющихся на реальных задачах: произвольная форма обрабатываемой области; сетку можно сделать более редкой в тех местах, где особая точность не нужна.

Долгое время широкому распространению МКЭ мешало отсутствие алгоритмов автоматического разбиения области на «почти равносторонние» треугольники (погрешность, в зависимости от вариации метода, обратно пропорциональна синусу или самого острого, или самого тупого угла в разбиении). Впрочем, эту задачу удалось успешно решить (алгоритмы основаны на триангуляции Делоне), что дало возможность создавать полностью автоматические конечноэлементные САПР.

История развития метода

Возникновение метода конечных элементов связано с решением задач космических исследований в 1950-х годах. Идея МКЭ была разработана в СССР ещё в 1936 году, но из-за неразвитости вычислительной техники метод не получил развития, поэтому впервые был применён на ЭВМ лишь в 1944 году Аргирисом. Этот метод возник из строительной механики и теории упругости, а уже затем было получено его математическое обоснование. Существенный толчок в своём развитии МКЭ получил в 1963 году после того, как было доказано то, что его можно рассматривать как один из вариантов распространённого в строительной механике метода Рэлея — Ритца, который путём минимизации потенциальной энергии сводит задачу к системе линейных уравнений равновесия. После того, как была установлена связь МКЭ с процедурой минимизации, он стал применяться к задачам, описываемым уравнениями Лапласа или Пуассона. Область применения МКЭ значительно расширилась, когда было установлено (в 1968 году), что уравнения, определяющие элементы в задачах, могут быть легко получены с помощью вариантов метода взвешенных невязок, таких как метод Галёркина или метод наименьших квадратов. Это сыграло важную роль в теоретическом обосновании МКЭ, так как позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений.

С развитием вычислительных средств возможности метода постоянно расширяются, также расширяется и класс решаемых задач. В настоящее время предложено большое количество реализаций метода конечных элементов при моделировании процессов диффузии, теплопроводности, гидродинамики, механики, электродинамики и др.

См. также

• Метод дискретного элемента
• Метод конечных разностей
• Метод конечных объёмов
• Метод подвижных клеточных автоматов
• Метод граничного элемента

Литература

• Галлагер Р. Метод конечных элементов. Основы: Пер. с англ. — М.: Мир, 1984
• Деклу Ж. Метод конечных элементов: Пер. с франц. — М.: Мир, 1976
• Зенкевич О. Метод конечных элементов в технике — М.: Мир, 1975.
• Зенкевич О., Морган К. Конечные элементы и аппроксимация: Пер. с англ. — М.: Мир, 1986
• Сегерлинд Л. Применение метода конечных элементов — М.: Мир, 1979. — 392 С.

Ссылки

• [www.exponenta.ru/educat/systemat/smirnov/main.asp Метод конечных элементов, В. В. Смирнов (Бийский технологический институт)]
• Боровков А.И. и др. [www.FEA.ru/modules.php?name=Info&pid=196 Компьютерный инжиниринг. Аналитический обзор - учебное пособие]. — СПб.: Изд-во Политехн. ун-та, 2012. — 93 с. — ISBN 978-5-7422-3766-2.