Теорема Пифагора

Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы.

Соотношение в том или ином виде предположительно было известно различным древним цивилизациям задолго до нашей эры; первое геометрическое доказательство приписывается Пифагору, строгое аксиоматическое доказательство утверждения принадлежит Евклиду.

Также может быть выражена как геометрический факт о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. Верно и обратное утверждение: треугольник, сумма квадратов длин двух сторон которого равна квадрату длины третей стороны, является прямоугольным.

Существует ряд обобщений для произвольных треугольников, для фигур в пространствах высших размерностей, сводящихся к основному утверждению теоремы при рассмотрении прямоугольного треугольника. В неевклидовых геометриях теорема не выполняется.

История

По мнению историка математики Морица Кантора в Древнем Египте во времена царя Аменемхета I (около XXIII век до н. э.) было известно о прямоугольном треугольнике со сторонами 3, 4, 5 — его использовали гарпедонапты — «натягиватели верёвок». В древневавилонском тексте, относимом ко временам Хаммурапи (XX век до н. э.), приведено приближённое вычисление гипотенузы. По мнению Ван-дер-Вардена, очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.

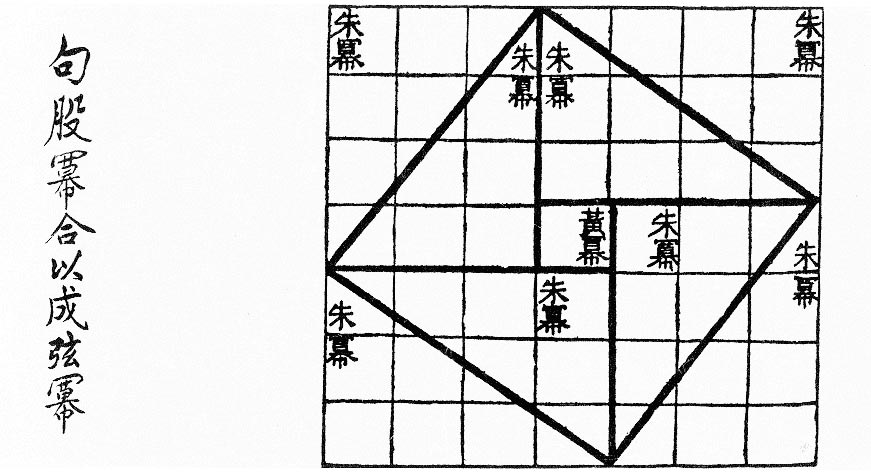В древнекитайской книге Чжоу би суань цзин (кит. 周髀算經), относимой к периоду V—III веков до н. э., приводится треугольник со сторонами 3, 4 и 5, притом изображение можно трактовать как графическое обоснование соотношения теоремы.

Общепринято, что доказательство соотношения дано древнегреческим философом Пифагором (570—490 до н. э.). Имеется свидетельство Прокла (485—410 до н. э.), что Пифагор использовал алгебраические методы, чтобы находить пифагоровы тройки, но при этом в течении пяти веков после смерти Пифагора прямых упоминаний о доказательстве его авторства не находится. Однако, когда такие авторы как Плутарх и Цицерон пишут о теореме Пифагора, из содержания следует, будто авторство Пифагора общеизвестно и несомненно:. Существует предание, сообщённое Диогеном Лаэртским, согласно которому Пифагор якобы отпраздновал открытие своей теоремы гигантским пиром, заклав на радостях сотню быков.

Приблизительно в 400 году до н. э., согласно Проклу, Платон дал метод нахождения пифагоровых троек, сочетающий алгебру и геометрию. Около в 300 года до н. э. в «Началах» Евклида появилось старейшее аксиоматическое доказательство теоремы Пифагора.

Формулировки

Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике, длины катетов которого равны <math>a</math> и <math>b</math>, а длина гипотенузы — <math>c</math>, выполнено соотношение:

<math>a^2 + b^2 = c^2</math>.

Возможна и эквивалентная геометрическая формулировка, прибегающая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Обратная теорема Пифагора — утверждение о прямоугольности всякого треугольника, длины сторон которого связаны соотношением <math>a^2 + b^2 = c^2</math>. Как следствие, для всякой тройки положительных чисел <math>a</math>, <math>b</math> и <math>c</math>, такой, что <math>a^2 + b^2 = c^2</math>, существует прямоугольный треугольник с катетами <math>a</math> и <math>b</math> и гипотенузой <math>c</math>.

Доказательства

В научной литературе зафиксировано не менее 367 доказательств теоремы Пифагора, что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия), метод площадей, существуют также различные экзотические доказательства (например, с помощью дифференциальных уравнений).

Через подобные треугольники

Одним из наиболее популярных в учебной литературе доказательств алгебраической формулировки является доказательство с использованием техники подобия треугольников, при этом оно почти непосредственно выводится из аксиом и не задействует понятие площади фигуры. В нём для треугольника <math>\triangle ABC</math> с прямым углом при вершине <math>C</math> со сторонами <math>a, b, c</math>, противолежащими вершинам <math>A, B, C</math> соответственно, проводится высота <math>CH</math>, при этом (согласно признаку подобия по равенству двух углов) возникают соотношения подобия: <math>\triangle ABC \sim \triangle ACH</math> и <math>\triangle ABC \sim \triangle CBH</math>, из чего непосредственно следуют соотношения:

<math> \frac{a}{c}=\frac{|HB|}{a}</math>; <math>\frac{b}{c}=\frac{|AH|}{b}</math>.

При перемножении крайних членов пропорций выводятся равенства:

<math>a^2=c\cdot |HB|</math>; <math>b^2=c\cdot |AH|</math>,

покомпонентное сложение которых даёт требуемый результат:

<math>a^2+b^2=c\cdot\left(|HB|+|AH|\right)=c^2 \, \Leftrightarrow \, a^2+b^2=c^2</math>.

Доказательства методом площадей

Большое число доказательств задействуют понятие площади. Несмотря на видимую простоту многих из них, такие доказательства используют свойства площадей фигур, доказательства которых сложнее доказательства самой теоремы Пифагора.

Доказательство через равнодополняемость

Доказательство через равнодополняемость использует четыре копии прямоугольного треугольника с катетами <math>a, b</math> и гипотенузой <math>c</math>, расположенные таким образом, чтобы образовывать квадрат со стороной <math>a+b</math> и внутренний четырёхугольник со сторонами длиной <math>c</math>. Внутренний четырёхугольник в этой конфигурации является квадратом, так как сумма двух противоположных прямому острых углов — 90°, а развёрнутый угол — 180°. Площадь внешнего квадрата равна <math>(a+b)^2</math>, он состоит из внутреннего квадрата площадью <math>c^2</math> и четырёх прямоугольных треугольников, каждый площадью <math>\frac{ab}{2}</math>, в результате из соотношения <math>(a+b)^2=4\cdot\frac{ab}{2}+c^2</math> при алгебраическом преобразовании следует утверждение теоремы.

Доказательство Евклида

Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами.

Конструкция, используемая для доказательства следующая: для прямоугольного треугольника <math>\triangle ABC</math> с прямым углом <math>C</math>, квадратов над катетами <math>ACED</math> и <math>BCFG</math> и квадрата над гипотенузой <math>ABIK</math> строится высота <math>CH</math> и продолжающий её луч <math>s</math>, разбивающий квадрат над гипотенузой на два прямоугольника <math>AHJK</math> и <math>BHJI</math>. Доказательство нацелено на установление равенства площадей прямоугольника <math>AHJK</math> с квадратом над катетом <math>AC</math>; равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом устанавливается аналогичным образом.

Равенство площадей прямоугольника <math>AHJK</math> и <math>ACED</math> устанавливается через конгруэнтность треугольников <math>\triangle ACK</math> и <math>\triangle ABD</math>, площадь каждого из которых равна половине площади квадратов <math>AHJK</math> и <math>ACED</math> соответственно в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если у фигур есть общая сторона, а высота треугольника к общей стороне является другой стороной прямоугольника. Конгруэнтность треугольников следует из равенства двух сторон (стороны квадратов) и углу между ними (составленного из прямой угла и угла при <math>A</math>.

Таким образом, доказательством устанавливается, что площадь квадрата над гипотенузой, составленного из прямоугольников <math>AHJK</math> и <math>BHJI</math>, равна сумме площадей квадратов над катетами.

Доказательство Леонардо да Винчи

К методу площадей относится также доказательство, найденное Леонардо да Винчи. В нём для прямоугольного треугольника <math>\triangle ABC</math> с прямым углом <math>C</math>, квадратов над катетами <math>ACED</math> и <math>BCFG</math> и квадрата над гипотенузой <math>ABIK</math>, над стороной <math>IK</math> последнего во внешнюю сторону строится треугольник, конгруэнтный <math>\triangle ABC</math>, притом отражённый как относительно гипотенузы, так относительно высоты к ней (то есть <math>JI = BC</math> и <math>HI = AC</math>). Прямая <math>CI</math> разбивает квадрат над гипотенузой на две равные части, поскольку треугольники <math>\triangle ABC</math> и <math>\triangle JHI</math> равны по построению. Доказательство устанавливает конгруэнтность четырёхугольников <math>CAJI</math> и <math>DABG</math>, площадь каждого из которых, оказывается, с одной стороны, равной сумме половин площадей квадратов над катетами и площади исходного треугольника, с другой стороны — половине площади квадрата над гипотенузой плюс площадь исходного треугольника. Итого, половина суммы площадей квадратов над катетами равна половине площади квадрата над гипотенузой, что равносильно геометрической формулировке теоремы Пифагора.

Доказательство методом бесконечно малых

Существует несколько доказательств, прибегающих к технике дифференциальных уравнений. В частности, Харди приписывается доказательство, использующее бесконечно малые приращения катетов <math>a</math> и <math>b</math> и гипотенузы <math>c</math>, и сохраняющие подобие с исходным прямоугольником, то есть, обеспечивающие выполнение следующих дифференциальных соотношений:

<math>\frac {da}{dc} = \frac {c}{a}</math>, <math>\frac {db}{dc} = \frac {c}{b}</math>.

Методом разделения переменных из них выводится дифференциальное уравнение <math>c\ dc = a\, da + b\, db</math>, интегрирование которого даёт соотношение <math>c^2 = a^2 +b^2 + \mathrm{Const}</math>. Применение начальных условий <math>a = b = c = 0</math> определяет константу как 0, что в результате даёт утверждение теоремы.

Квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.

Вариации и обобщения

Подобные геометрические фигуры на трёх сторонах

Важное геометрическое обобщение теоремы Пифагора дал Евклид в «Началах», перейдя от площадей квадратов на сторонах к площадям произвольных подобных геометрических фигур: сумма площадей таких фигур, построенных на катетах, будет равна площади подобной им фигуры, построенной на гипотенузе.

Главная идея этого обобщения заключается в том, что площадь подобной геометрической фигуры пропорциональна квадрату любого своего линейного размера и в частности квадрату длины любой стороны. Следовательно, для подобных фигур с площадями <math>A</math>, <math>B</math> и <math>C</math>, построенных на катетах с длинами <math>a</math> и <math>b</math> и гипотенузе <math>c</math> соответственно, имеет место соотношение:

<math>\frac{A}{a^2} = \frac{B}{b^2} = \frac{C}{c^2}\, \Rightarrow \, A + B = \frac{a^2}{c^2}C + \frac{b^2}{c^2}C</math>.

Так как по теореме Пифагора <math>a^2 + b^2 = c^2</math>, то выполнено <math>A + B = C</math>.

Кроме того, если возможно доказать без привлечения теоремы Пифагора, что для площадей трёх подобных геометрических фигур на сторонах прямоугольного треугольника выполнено соотношение <math>A + B = C</math>, то с использованием обратного хода доказательства обобщения Евклида можно вывести доказательство теоремы Пифагора. Например, если на гипотенузе построить конгруэтный начальному прямоугольный треугольник площадью <math>C</math>, а на катетах — два подобных ему прямоугольных треугольника с площадями <math>A</math> и <math>B</math>, то оказывается, что треугольники на катетах образуются в результате деления начального треугольника его высотой, то есть сумма двух меньших площадей треугольников равна площади третьего, таким образом <math>A + B = C</math> и, применяя соотношение для подобных фигур, выводится теорема Пифагора.

Теорема косинусов

Теорема Пифагора — это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике:

<math>a^2+b^2-2ab\cos{\theta}=c^2</math>,

где <math>\theta</math> — угол между сторонами <math>a</math> и <math>b</math>. Если угол равен 90°, то <math>\cos \theta = 0</math>, и формула упрощается до обычной теоремы Пифагора.

Произвольный треугольник

Существует обобщение теоремы Пифагора на произвольный треугольник, оперирующее исключительно соотношением длин сторон, считается, что оно впервые было установлено сабийским астроном Сабитом ибн Куррой. В нём для произвольного треугольника со сторонами <math>a, b, c</math> в него вписывается равнобедренный треугольник с основанием на стороне <math>c</math>, вершиной, совпадающей с вершиной исходного треугольника, противолежащей стороне <math>c</math> и углами при основании, равными углу <math>\theta</math>, противолежащему стороне <math>c</math>. В результате образуются два треугольника, подобных исходному: первый — со сторонами <math>a</math>, дальней от неё боковой стороной вписанного равнобедренного треугольника, и <math>r</math> — части стороны <math>c</math>; второй — симметрично к нему от стороны <math>b</math> со стороной <math>s</math> — соответствующей частью стороны <math>c</math>. В результате оказывается выполнено соотношение:

<math> a^2 +b^2 =c(r+s) </math>,

вырождающееся в теорему Пифагора при <math>\theta=\pi/2</math>. Соотношение является следствием подобия образованных треугольников:

<math>\frac{c}{a} = \frac{a}{r}, \, \frac{c}{b} = \frac{b}{s} \, \Rightarrow \, cr +cs = a^2 +b^2</math>.

Теорема Паппа о площадях

Теорема Паппа о площадях, позволяющая для произвольного треугольника и произвольных параллелограммов на двух его сторонах построить параллелограмм на третьей стороне таким образом, чтобы его площадь была равна сумме площадей двух заданных параллелограммов, также может быть рассмотрена как обобщение теоремы Пифагора: в случае, когда исходный треугольник — прямоугольный, а на катетах в качестве параллелограммов заданы квадраты, квадрат, построенный на гипотенузе оказывается удовлетворяющим условиям теоремы Паппа о площадях.

Многомерные обобщения

Обобщением теоремы Пифагора для трёхмерного евклидова пространства является теорема де Гуа: если тетраэдр имеет прямой угол, то квадрат площади грани, лежащей напротив прямого угла, равен сумме квадратов площадей других трёх граней. Этот вывод может быть обобщен и как «n-мерная теорема Пифагора» для евклидовых пространств высших размерностей — для граней ортогонального <math>n</math>-мерного симплекса с площадями <math>S_1, \dots, S_n</math> ортогональных граней и противолежащей им грани площадью <math>S_0</math> выполнено соотношение:

<math>S_0^2 = \sum_{i=1}^n S_i^2</math>.

Ещё одно многомерное обобщение возникает из задачи нахождения квадрата длины диагонали прямоугольного параллелепипеда: для её вычисления необходимо дважды применить теорему Пифагора, в результате она составит сумму квадратов длин трёх смежных сторон параллелепипеда. В общем случае, длина диагонали <math>n</math>-мерного прямоугольного параллелепипеда со смежными сторонами с длинами <math>a_1, \dots, a_n</math> составляет:

<math>d^2 = \sum_{i=1}^n a_i^2</math>,

как и в трёхмерном случае, результат является следствием последовательного применения теоремы Пифагора к прямоугольным треугольникам в перпендикулярных плоскостях.

Неевклидова геометрия

Теорема Пифагора выводится из аксиом евклидовой геометрии и недействительна для неевклидовой геометрии — выполнение теоремы Пифагора равносильно постулату Евклида о параллельности.

В неевклидовой геометрии соотношение между сторонами прямоугольного треугольника обязательно будет в форме, отличной от теоремы Пифагора. Например, в сферической геометрии все три стороны прямоугольного треугольника, которые ограничивают собой октант единичной сферы, имеют длину <math>pi/2</math>, что противоречит теореме Пифагора.

При этом теорема Пифагора справедлива в гиперболической и эллиптической геометрии, если требование о прямоугольности треугольника заменить условием, что сумма двух углов треугольника должна равняться третьему.

Сферическая геометрия

Для любого прямоугольного треугольника на сфере радиусом <math>R</math> (например, если угол <math>\gamma</math> в треугольнике прямой) со сторонами <math>a, b, c</math> соотношение между сторонами имеет вид:

<math> \cos \left(\frac{c}{R}\right)=\cos \left(\frac{a}{R}\right) \cdot \cos \left(\frac{b}{R}\right)</math>.

Это равенство может быть выведено как особый случай сферической теоремы косинусов, которая справедлива для всех сферических треугольников:

<math> \cos \left(\frac{c}{R}\right)=\cos \left(\frac{a}{R}\right) \cdot \cos \left(\frac{b}{R}\right) + \sin\left(\frac{a}{R}\right) \cdot \sin\left(\frac{b}{R}\right) \cdot \cos \gamma</math>.

Применяя ряд Тейлора в функции косинуса (<math>\cos x \approx 1 - \dfrac{x^2}{2}</math>) можно показать, что если радиус <math>R</math> стремится к бесконечности, а аргументы <math>\dfrac{a}{R}</math>, <math>\dfrac{b}{R}</math> и <math>\dfrac{c}{R}</math> стремятся к нулю, то сферическое соотношение между сторонами в прямоугольном треугольнике приближается к теореме Пифагора.

Геометрия Лобачевского

В геометрии Лобачевского для прямоугольного треугольника со сторонами <math>a, b, c</math> со стороной <math>c</math>, противолежащей прямому углу, соотношение между сторонами будет следующим:

<math> \operatorname{ch} c=\operatorname{ch} a \cdot \operatorname{ch} b</math>,

где <math> \operatorname{ch}</math> — гиперболический косинус. Эта формула является частным случаем гиперболической теоремы косинусов, которая справедлива для всех треугольников:

<math>\operatorname{ch}c= \operatorname{ch} a \cdot \operatorname{ch} b - \operatorname{sh} a \cdot \operatorname{sh} b \cdot \cos \gamma </math>,

где <math>\gamma</math> — угол, вершина которого противоположна стороне <math>c</math>.

Используя ряд Тейлора для гиперболического косинуса (<math>\operatorname{ch}x \approx 1 + x^2 / 2</math>) можно показать, что если гиперболический треугольник уменьшается (то есть, когда <math>a</math>, <math>b</math> и <math>c</math> стремятся к нулю), то гиперболические соотношения в прямоугольном треугольнике приближаются к соотношению классической теоремы Пифагора.

Применение

Расстояние в двумерных прямоугольных системах

Важнейшее применение теоремы Пифагора — определение расстояния между двумя точками в прямоугольной системе координат: расстояние <math>s</math> между точками с координатами <math>(a, b)</math> и <math>(c, d)</math> равно:

<math>s = \sqrt{(a-c)^2 + (b-d)^2}</math>.

Для комплексных чисел теорема Пифагора даёт естественную формулу для нахождения модуля комплексного числа — для <math>z=x+yi</math> он равен длине радиус-вектора на комплексной плоскости к точке <math>(x, y)</math>:

<math>|z| = \sqrt{x^2 + y^2}</math>.

Расстояние между комплексными числами <math>z_1 = x_1+y_1i</math> и <math>z_1 = x_1+y_1i</math> также представляется в форме теоремы Пифагора:

<math>|z_1 - z_2| = \sqrt{(x_1-x_2)^2 + (y_2-y_2)^2}</math>.

Евклидова метрика

Евклидова метрика — функция расстояния в евклидовых пространствах, определяемая по теореме Пифагора, непосредственным её примененем в двумерном случае, и последовательным в многомерном; для точек <math>n</math>-мерного пространства <math>p = (p_1, \dots, p_n)</math> и <math>q = (q_1, \dots, q_n)</math> расстояние <math>d(p, q)</math> между ними определяется следующим образом:

<math>d(p, q) = \sqrt{\sum_{i=1}^n{(p_i - q_i)^2}}</math>.

Теория чисел

Пифагорова тройка — набор из трёх натуральных чисел <math>(x,\;y,\;z)</math>, которые могут быть длинами сторон прямоугольного треугольника, то есть натуральные числа, удовлетворяющие диофантову уравнению <math>x^2 + y^2 = z^2</math>. Пифагоровы тройки играют важную роль в теории чисел, задача их эффективного нахождения породила широкий пласт работ начиная с древнейших времён до вплоть до современности. Формулировка Великой теоремы Ферма аналогична задаче нахождения пифагоровых троек для степени более 2.

См. также

• Пифагорова мозаика

Литература

• Ван-дер-Варден Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. — М., 1959
• Глейзер Г. И. История математики в школе. — М., 1982
• Еленьский Щ. По следам Пифагора. — М., 1961
• Клауди Альсина. Секта чисел. Теорема Пифагора. — М.: Де Агостини, 2014. — 152 с. — (Мир математики: в 45 томах, том 5). — ISBN 978-5-9774-0633-8.
• Литцман В. [www.ega-math.narod.ru/Books/Pythagor.htm#ch1 Теорема Пифагора.] — М., 1960.
  • [th-pif.narod.ru/ Сайт о теореме Пифагора] с большим числом доказательств, материал взят из книги В. Литцмана, большое число чертежей представлено в виде отдельных графических файлов.
• Скопец З. А. Геометрические миниатюры. — М., 1990
• Euclid. The Elements (3 vols.) / Translated by Johan Ludvig Heiberg with an introduction and commentary by Thomas L. Heath. — Reprint of 1908. — Dover, 1956. — Vol. 1 (Books I and II). — ISBN 0-486-60088-2.
• Heath S. A History of Greek Mathematics (2 Vols.). — Edition of Dover Publications, Inc. (1981). — Clarendon Press, Oxford, 1921. — ISBN 0-486-24073-8.

Ссылки

• [www.moypifagor.narod.ru/history.htm История теоремы Пифагора]
• Г. Глейзер, академик РАО, Москва. [mat.1september.ru/2001/24/no24_01.htm О теореме Пифагора и способах её доказательства]
• Ролик серии «Математические этюды», посвящённый теореме Пифагора (для [www.etudes.ru/ru/mov/mov044/index.php компьютера], [itunes.apple.com/ru/app/id404430950 iPhone], [itunes.apple.com/ru/app/pythagoras-hd/id404432708 iPad])
• [www.mccme.ru/mmmf-lectures/books/books/books.php?book=3&page=2 Теорема Пифагора и пифагоровы тройки.] Глава из книги Д. В. Аносова «Взгляд на математику и нечто из неё»
• [mathworld.wolfram.com/PythagoreanTheorem.html Теорема Пифагора на WolframMathWorld] (англ.)
• [www.cut-the-knot.org/pythagoras/index.shtml Cut-The-Knot, секция, посвящённая теореме Пифагора, около 70 доказательств и обширная дополнительная информация] (англ.)

Отрывок, характеризующий Теорема Пифагора

В то время как князь Андрей ходил докладывать про багрового генерала, генерал этот, видимо, не разделявший понятий Бориса о выгодах неписанной субординации, так уперся глазами в дерзкого прапорщика, помешавшего ему договорить с адъютантом, что Борису стало неловко. Он отвернулся и с нетерпением ожидал, когда возвратится князь Андрей из кабинета главнокомандующего.
– Вот что, мой милый, я думал о вас, – сказал князь Андрей, когда они прошли в большую залу с клавикордами. – К главнокомандующему вам ходить нечего, – говорил князь Андрей, – он наговорит вам кучу любезностей, скажет, чтобы приходили к нему обедать («это было бы еще не так плохо для службы по той субординации», подумал Борис), но из этого дальше ничего не выйдет; нас, адъютантов и ординарцев, скоро будет батальон. Но вот что мы сделаем: у меня есть хороший приятель, генерал адъютант и прекрасный человек, князь Долгоруков; и хотя вы этого можете не знать, но дело в том, что теперь Кутузов с его штабом и мы все ровно ничего не значим: всё теперь сосредоточивается у государя; так вот мы пойдемте ка к Долгорукову, мне и надо сходить к нему, я уж ему говорил про вас; так мы и посмотрим; не найдет ли он возможным пристроить вас при себе, или где нибудь там, поближе .к солнцу.
Князь Андрей всегда особенно оживлялся, когда ему приходилось руководить молодого человека и помогать ему в светском успехе. Под предлогом этой помощи другому, которую он по гордости никогда не принял бы для себя, он находился вблизи той среды, которая давала успех и которая притягивала его к себе. Он весьма охотно взялся за Бориса и пошел с ним к князю Долгорукову.
Было уже поздно вечером, когда они взошли в Ольмюцкий дворец, занимаемый императорами и их приближенными.
В этот самый день был военный совет, на котором участвовали все члены гофкригсрата и оба императора. На совете, в противность мнения стариков – Кутузова и князя Шварцернберга, было решено немедленно наступать и дать генеральное сражение Бонапарту. Военный совет только что кончился, когда князь Андрей, сопутствуемый Борисом, пришел во дворец отыскивать князя Долгорукова. Еще все лица главной квартиры находились под обаянием сегодняшнего, победоносного для партии молодых, военного совета. Голоса медлителей, советовавших ожидать еще чего то не наступая, так единодушно были заглушены и доводы их опровергнуты несомненными доказательствами выгод наступления, что то, о чем толковалось в совете, будущее сражение и, без сомнения, победа, казались уже не будущим, а прошедшим. Все выгоды были на нашей стороне. Огромные силы, без сомнения, превосходившие силы Наполеона, были стянуты в одно место; войска были одушевлены присутствием императоров и рвались в дело; стратегический пункт, на котором приходилось действовать, был до малейших подробностей известен австрийскому генералу Вейротеру, руководившему войска (как бы счастливая случайность сделала то, что австрийские войска в прошлом году были на маневрах именно на тех полях, на которых теперь предстояло сразиться с французом); до малейших подробностей была известна и передана на картах предлежащая местность, и Бонапарте, видимо, ослабленный, ничего не предпринимал.
Долгоруков, один из самых горячих сторонников наступления, только что вернулся из совета, усталый, измученный, но оживленный и гордый одержанной победой. Князь Андрей представил покровительствуемого им офицера, но князь Долгоруков, учтиво и крепко пожав ему руку, ничего не сказал Борису и, очевидно не в силах удержаться от высказывания тех мыслей, которые сильнее всего занимали его в эту минуту, по французски обратился к князю Андрею.
– Ну, мой милый, какое мы выдержали сражение! Дай Бог только, чтобы то, которое будет следствием его, было бы столь же победоносно. Однако, мой милый, – говорил он отрывочно и оживленно, – я должен признать свою вину перед австрийцами и в особенности перед Вейротером. Что за точность, что за подробность, что за знание местности, что за предвидение всех возможностей, всех условий, всех малейших подробностей! Нет, мой милый, выгодней тех условий, в которых мы находимся, нельзя ничего нарочно выдумать. Соединение австрийской отчетливости с русской храбростию – чего ж вы хотите еще?
– Так наступление окончательно решено? – сказал Болконский.
– И знаете ли, мой милый, мне кажется, что решительно Буонапарте потерял свою латынь. Вы знаете, что нынче получено от него письмо к императору. – Долгоруков улыбнулся значительно.
– Вот как! Что ж он пишет? – спросил Болконский.
– Что он может писать? Традиридира и т. п., всё только с целью выиграть время. Я вам говорю, что он у нас в руках; это верно! Но что забавнее всего, – сказал он, вдруг добродушно засмеявшись, – это то, что никак не могли придумать, как ему адресовать ответ? Ежели не консулу, само собою разумеется не императору, то генералу Буонапарту, как мне казалось.
– Но между тем, чтобы не признавать императором, и тем, чтобы называть генералом Буонапарте, есть разница, – сказал Болконский.
– В том то и дело, – смеясь и перебивая, быстро говорил Долгоруков. – Вы знаете Билибина, он очень умный человек, он предлагал адресовать: «узурпатору и врагу человеческого рода».
Долгоруков весело захохотал.
– Не более того? – заметил Болконский.
– Но всё таки Билибин нашел серьезный титул адреса. И остроумный и умный человек.
– Как же?
– Главе французского правительства, au chef du gouverienement francais, – серьезно и с удовольствием сказал князь Долгоруков. – Не правда ли, что хорошо?
– Хорошо, но очень не понравится ему, – заметил Болконский.
– О, и очень! Мой брат знает его: он не раз обедал у него, у теперешнего императора, в Париже и говорил мне, что он не видал более утонченного и хитрого дипломата: знаете, соединение французской ловкости и итальянского актерства? Вы знаете его анекдоты с графом Марковым? Только один граф Марков умел с ним обращаться. Вы знаете историю платка? Это прелесть!
И словоохотливый Долгоруков, обращаясь то к Борису, то к князю Андрею, рассказал, как Бонапарт, желая испытать Маркова, нашего посланника, нарочно уронил перед ним платок и остановился, глядя на него, ожидая, вероятно, услуги от Маркова и как, Марков тотчас же уронил рядом свой платок и поднял свой, не поднимая платка Бонапарта.
– Charmant, [Очаровательно,] – сказал Болконский, – но вот что, князь, я пришел к вам просителем за этого молодого человека. Видите ли что?…
Но князь Андрей не успел докончить, как в комнату вошел адъютант, который звал князя Долгорукова к императору.
– Ах, какая досада! – сказал Долгоруков, поспешно вставая и пожимая руки князя Андрея и Бориса. – Вы знаете, я очень рад сделать всё, что от меня зависит, и для вас и для этого милого молодого человека. – Он еще раз пожал руку Бориса с выражением добродушного, искреннего и оживленного легкомыслия. – Но вы видите… до другого раза!
Бориса волновала мысль о той близости к высшей власти, в которой он в эту минуту чувствовал себя. Он сознавал себя здесь в соприкосновении с теми пружинами, которые руководили всеми теми громадными движениями масс, которых он в своем полку чувствовал себя маленькою, покорною и ничтожной» частью. Они вышли в коридор вслед за князем Долгоруковым и встретили выходившего (из той двери комнаты государя, в которую вошел Долгоруков) невысокого человека в штатском платье, с умным лицом и резкой чертой выставленной вперед челюсти, которая, не портя его, придавала ему особенную живость и изворотливость выражения. Этот невысокий человек кивнул, как своему, Долгорукому и пристально холодным взглядом стал вглядываться в князя Андрея, идя прямо на него и видимо, ожидая, чтобы князь Андрей поклонился ему или дал дорогу. Князь Андрей не сделал ни того, ни другого; в лице его выразилась злоба, и молодой человек, отвернувшись, прошел стороной коридора.
– Кто это? – спросил Борис.
– Это один из самых замечательнейших, но неприятнейших мне людей. Это министр иностранных дел, князь Адам Чарторижский.
– Вот эти люди, – сказал Болконский со вздохом, который он не мог подавить, в то время как они выходили из дворца, – вот эти то люди решают судьбы народов.
На другой день войска выступили в поход, и Борис не успел до самого Аустерлицкого сражения побывать ни у Болконского, ни у Долгорукова и остался еще на время в Измайловском полку.


На заре 16 числа эскадрон Денисова, в котором служил Николай Ростов, и который был в отряде князя Багратиона, двинулся с ночлега в дело, как говорили, и, пройдя около версты позади других колонн, был остановлен на большой дороге. Ростов видел, как мимо его прошли вперед казаки, 1 й и 2 й эскадрон гусар, пехотные батальоны с артиллерией и проехали генералы Багратион и Долгоруков с адъютантами. Весь страх, который он, как и прежде, испытывал перед делом; вся внутренняя борьба, посредством которой он преодолевал этот страх; все его мечтания о том, как он по гусарски отличится в этом деле, – пропали даром. Эскадрон их был оставлен в резерве, и Николай Ростов скучно и тоскливо провел этот день. В 9 м часу утра он услыхал пальбу впереди себя, крики ура, видел привозимых назад раненых (их было немного) и, наконец, видел, как в середине сотни казаков провели целый отряд французских кавалеристов. Очевидно, дело было кончено, и дело было, очевидно небольшое, но счастливое. Проходившие назад солдаты и офицеры рассказывали о блестящей победе, о занятии города Вишау и взятии в плен целого французского эскадрона. День был ясный, солнечный, после сильного ночного заморозка, и веселый блеск осеннего дня совпадал с известием о победе, которое передавали не только рассказы участвовавших в нем, но и радостное выражение лиц солдат, офицеров, генералов и адъютантов, ехавших туда и оттуда мимо Ростова. Тем больнее щемило сердце Николая, напрасно перестрадавшего весь страх, предшествующий сражению, и пробывшего этот веселый день в бездействии.
– Ростов, иди сюда, выпьем с горя! – крикнул Денисов, усевшись на краю дороги перед фляжкой и закуской.
Офицеры собрались кружком, закусывая и разговаривая, около погребца Денисова.
– Вот еще одного ведут! – сказал один из офицеров, указывая на французского пленного драгуна, которого вели пешком два казака.
Один из них вел в поводу взятую у пленного рослую и красивую французскую лошадь.
– Продай лошадь! – крикнул Денисов казаку.
– Изволь, ваше благородие…
Офицеры встали и окружили казаков и пленного француза. Французский драгун был молодой малый, альзасец, говоривший по французски с немецким акцентом. Он задыхался от волнения, лицо его было красно, и, услыхав французский язык, он быстро заговорил с офицерами, обращаясь то к тому, то к другому. Он говорил, что его бы не взяли; что он не виноват в том, что его взяли, а виноват le caporal, который послал его захватить попоны, что он ему говорил, что уже русские там. И ко всякому слову он прибавлял: mais qu'on ne fasse pas de mal a mon petit cheval [Но не обижайте мою лошадку,] и ласкал свою лошадь. Видно было, что он не понимал хорошенько, где он находится. Он то извинялся, что его взяли, то, предполагая перед собою свое начальство, выказывал свою солдатскую исправность и заботливость о службе. Он донес с собой в наш арьергард во всей свежести атмосферу французского войска, которое так чуждо было для нас.
Казаки отдали лошадь за два червонца, и Ростов, теперь, получив деньги, самый богатый из офицеров, купил ее.
– Mais qu'on ne fasse pas de mal a mon petit cheval, – добродушно сказал альзасец Ростову, когда лошадь передана была гусару.
Ростов, улыбаясь, успокоил драгуна и дал ему денег.
– Алё! Алё! – сказал казак, трогая за руку пленного, чтобы он шел дальше.
– Государь! Государь! – вдруг послышалось между гусарами.
Всё побежало, заторопилось, и Ростов увидал сзади по дороге несколько подъезжающих всадников с белыми султанами на шляпах. В одну минуту все были на местах и ждали. Ростов не помнил и не чувствовал, как он добежал до своего места и сел на лошадь. Мгновенно прошло его сожаление о неучастии в деле, его будничное расположение духа в кругу приглядевшихся лиц, мгновенно исчезла всякая мысль о себе: он весь поглощен был чувством счастия, происходящего от близости государя. Он чувствовал себя одною этою близостью вознагражденным за потерю нынешнего дня. Он был счастлив, как любовник, дождавшийся ожидаемого свидания. Не смея оглядываться во фронте и не оглядываясь, он чувствовал восторженным чутьем его приближение. И он чувствовал это не по одному звуку копыт лошадей приближавшейся кавалькады, но он чувствовал это потому, что, по мере приближения, всё светлее, радостнее и значительнее и праздничнее делалось вокруг него. Всё ближе и ближе подвигалось это солнце для Ростова, распространяя вокруг себя лучи кроткого и величественного света, и вот он уже чувствует себя захваченным этими лучами, он слышит его голос – этот ласковый, спокойный, величественный и вместе с тем столь простой голос. Как и должно было быть по чувству Ростова, наступила мертвая тишина, и в этой тишине раздались звуки голоса государя.
– Les huzards de Pavlograd? [Павлоградские гусары?] – вопросительно сказал он.
– La reserve, sire! [Резерв, ваше величество!] – отвечал чей то другой голос, столь человеческий после того нечеловеческого голоса, который сказал: Les huzards de Pavlograd?
Государь поровнялся с Ростовым и остановился. Лицо Александра было еще прекраснее, чем на смотру три дня тому назад. Оно сияло такою веселостью и молодостью, такою невинною молодостью, что напоминало ребяческую четырнадцатилетнюю резвость, и вместе с тем это было всё таки лицо величественного императора. Случайно оглядывая эскадрон, глаза государя встретились с глазами Ростова и не более как на две секунды остановились на них. Понял ли государь, что делалось в душе Ростова (Ростову казалось, что он всё понял), но он посмотрел секунды две своими голубыми глазами в лицо Ростова. (Мягко и кротко лился из них свет.) Потом вдруг он приподнял брови, резким движением ударил левой ногой лошадь и галопом поехал вперед.
Молодой император не мог воздержаться от желания присутствовать при сражении и, несмотря на все представления придворных, в 12 часов, отделившись от 3 й колонны, при которой он следовал, поскакал к авангарду. Еще не доезжая до гусар, несколько адъютантов встретили его с известием о счастливом исходе дела.
Сражение, состоявшее только в том, что захвачен эскадрон французов, было представлено как блестящая победа над французами, и потому государь и вся армия, особенно после того, как не разошелся еще пороховой дым на поле сражения, верили, что французы побеждены и отступают против своей воли. Несколько минут после того, как проехал государь, дивизион павлоградцев потребовали вперед. В самом Вишау, маленьком немецком городке, Ростов еще раз увидал государя. На площади города, на которой была до приезда государя довольно сильная перестрелка, лежало несколько человек убитых и раненых, которых не успели подобрать. Государь, окруженный свитою военных и невоенных, был на рыжей, уже другой, чем на смотру, энглизированной кобыле и, склонившись на бок, грациозным жестом держа золотой лорнет у глаза, смотрел в него на лежащего ничком, без кивера, с окровавленною головою солдата. Солдат раненый был так нечист, груб и гадок, что Ростова оскорбила близость его к государю. Ростов видел, как содрогнулись, как бы от пробежавшего мороза, сутуловатые плечи государя, как левая нога его судорожно стала бить шпорой бок лошади, и как приученная лошадь равнодушно оглядывалась и не трогалась с места. Слезший с лошади адъютант взял под руки солдата и стал класть на появившиеся носилки. Солдат застонал.
– Тише, тише, разве нельзя тише? – видимо, более страдая, чем умирающий солдат, проговорил государь и отъехал прочь.
Ростов видел слезы, наполнившие глаза государя, и слышал, как он, отъезжая, по французски сказал Чарторижскому:
– Какая ужасная вещь война, какая ужасная вещь! Quelle terrible chose que la guerre!
Войска авангарда расположились впереди Вишау, в виду цепи неприятельской, уступавшей нам место при малейшей перестрелке в продолжение всего дня. Авангарду объявлена была благодарность государя, обещаны награды, и людям роздана двойная порция водки. Еще веселее, чем в прошлую ночь, трещали бивачные костры и раздавались солдатские песни.
Денисов в эту ночь праздновал производство свое в майоры, и Ростов, уже довольно выпивший в конце пирушки, предложил тост за здоровье государя, но «не государя императора, как говорят на официальных обедах, – сказал он, – а за здоровье государя, доброго, обворожительного и великого человека; пьем за его здоровье и за верную победу над французами!»
– Коли мы прежде дрались, – сказал он, – и не давали спуску французам, как под Шенграбеном, что же теперь будет, когда он впереди? Мы все умрем, с наслаждением умрем за него. Так, господа? Может быть, я не так говорю, я много выпил; да я так чувствую, и вы тоже. За здоровье Александра первого! Урра!
– Урра! – зазвучали воодушевленные голоса офицеров.
И старый ротмистр Кирстен кричал воодушевленно и не менее искренно, чем двадцатилетний Ростов.
Когда офицеры выпили и разбили свои стаканы, Кирстен налил другие и, в одной рубашке и рейтузах, с стаканом в руке подошел к солдатским кострам и в величественной позе взмахнув кверху рукой, с своими длинными седыми усами и белой грудью, видневшейся из за распахнувшейся рубашки, остановился в свете костра.
– Ребята, за здоровье государя императора, за победу над врагами, урра! – крикнул он своим молодецким, старческим, гусарским баритоном.
Гусары столпились и дружно отвечали громким криком.
Поздно ночью, когда все разошлись, Денисов потрепал своей коротенькой рукой по плечу своего любимца Ростова.
– Вот на походе не в кого влюбиться, так он в ца'я влюбился, – сказал он.
– Денисов, ты этим не шути, – крикнул Ростов, – это такое высокое, такое прекрасное чувство, такое…
– Ве'ю, ве'ю, д'ужок, и 'азделяю и одоб'яю…
– Нет, не понимаешь!
И Ростов встал и пошел бродить между костров, мечтая о том, какое было бы счастие умереть, не спасая жизнь (об этом он и не смел мечтать), а просто умереть в глазах государя. Он действительно был влюблен и в царя, и в славу русского оружия, и в надежду будущего торжества. И не он один испытывал это чувство в те памятные дни, предшествующие Аустерлицкому сражению: девять десятых людей русской армии в то время были влюблены, хотя и менее восторженно, в своего царя и в славу русского оружия.


На следующий день государь остановился в Вишау. Лейб медик Вилье несколько раз был призываем к нему. В главной квартире и в ближайших войсках распространилось известие, что государь был нездоров. Он ничего не ел и дурно спал эту ночь, как говорили приближенные. Причина этого нездоровья заключалась в сильном впечатлении, произведенном на чувствительную душу государя видом раненых и убитых.
На заре 17 го числа в Вишау был препровожден с аванпостов французский офицер, приехавший под парламентерским флагом, требуя свидания с русским императором. Офицер этот был Савари. Государь только что заснул, и потому Савари должен был дожидаться. В полдень он был допущен к государю и через час поехал вместе с князем Долгоруковым на аванпосты французской армии.
Как слышно было, цель присылки Савари состояла в предложении свидания императора Александра с Наполеоном. В личном свидании, к радости и гордости всей армии, было отказано, и вместо государя князь Долгоруков, победитель при Вишау, был отправлен вместе с Савари для переговоров с Наполеоном, ежели переговоры эти, против чаяния, имели целью действительное желание мира.
Ввечеру вернулся Долгоруков, прошел прямо к государю и долго пробыл у него наедине.
18 и 19 ноября войска прошли еще два перехода вперед, и неприятельские аванпосты после коротких перестрелок отступали. В высших сферах армии с полдня 19 го числа началось сильное хлопотливо возбужденное движение, продолжавшееся до утра следующего дня, 20 го ноября, в который дано было столь памятное Аустерлицкое сражение.
До полудня 19 числа движение, оживленные разговоры, беготня, посылки адъютантов ограничивались одной главной квартирой императоров; после полудня того же дня движение передалось в главную квартиру Кутузова и в штабы колонных начальников. Вечером через адъютантов разнеслось это движение по всем концам и частям армии, и в ночь с 19 на 20 поднялась с ночлегов, загудела говором и заколыхалась и тронулась громадным девятиверстным холстом 80 титысячная масса союзного войска.
Сосредоточенное движение, начавшееся поутру в главной квартире императоров и давшее толчок всему дальнейшему движению, было похоже на первое движение серединного колеса больших башенных часов. Медленно двинулось одно колесо, повернулось другое, третье, и всё быстрее и быстрее пошли вертеться колеса, блоки, шестерни, начали играть куранты, выскакивать фигуры, и мерно стали подвигаться стрелки, показывая результат движения.
Как в механизме часов, так и в механизме военного дела, так же неудержимо до последнего результата раз данное движение, и так же безучастно неподвижны, за момент до передачи движения, части механизма, до которых еще не дошло дело. Свистят на осях колеса, цепляясь зубьями, шипят от быстроты вертящиеся блоки, а соседнее колесо так же спокойно и неподвижно, как будто оно сотни лет готово простоять этою неподвижностью; но пришел момент – зацепил рычаг, и, покоряясь движению, трещит, поворачиваясь, колесо и сливается в одно действие, результат и цель которого ему непонятны.
Как в часах результат сложного движения бесчисленных различных колес и блоков есть только медленное и уравномеренное движение стрелки, указывающей время, так и результатом всех сложных человеческих движений этих 1000 русских и французов – всех страстей, желаний, раскаяний, унижений, страданий, порывов гордости, страха, восторга этих людей – был только проигрыш Аустерлицкого сражения, так называемого сражения трех императоров, т. е. медленное передвижение всемирно исторической стрелки на циферблате истории человечества.
Князь Андрей был в этот день дежурным и неотлучно при главнокомандующем.
В 6 м часу вечера Кутузов приехал в главную квартиру императоров и, недолго пробыв у государя, пошел к обер гофмаршалу графу Толстому.
Болконский воспользовался этим временем, чтобы зайти к Долгорукову узнать о подробностях дела. Князь Андрей чувствовал, что Кутузов чем то расстроен и недоволен, и что им недовольны в главной квартире, и что все лица императорской главной квартиры имеют с ним тон людей, знающих что то такое, чего другие не знают; и поэтому ему хотелось поговорить с Долгоруковым.
– Ну, здравствуйте, mon cher, – сказал Долгоруков, сидевший с Билибиным за чаем. – Праздник на завтра. Что ваш старик? не в духе?
– Не скажу, чтобы был не в духе, но ему, кажется, хотелось бы, чтоб его выслушали.
– Да его слушали на военном совете и будут слушать, когда он будет говорить дело; но медлить и ждать чего то теперь, когда Бонапарт боится более всего генерального сражения, – невозможно.
– Да вы его видели? – сказал князь Андрей. – Ну, что Бонапарт? Какое впечатление он произвел на вас?
– Да, видел и убедился, что он боится генерального сражения более всего на свете, – повторил Долгоруков, видимо, дорожа этим общим выводом, сделанным им из его свидания с Наполеоном. – Ежели бы он не боялся сражения, для чего бы ему было требовать этого свидания, вести переговоры и, главное, отступать, тогда как отступление так противно всей его методе ведения войны? Поверьте мне: он боится, боится генерального сражения, его час настал. Это я вам говорю.
– Но расскажите, как он, что? – еще спросил князь Андрей.
– Он человек в сером сюртуке, очень желавший, чтобы я ему говорил «ваше величество», но, к огорчению своему, не получивший от меня никакого титула. Вот это какой человек, и больше ничего, – отвечал Долгоруков, оглядываясь с улыбкой на Билибина.
– Несмотря на мое полное уважение к старому Кутузову, – продолжал он, – хороши мы были бы все, ожидая чего то и тем давая ему случай уйти или обмануть нас, тогда как теперь он верно в наших руках. Нет, не надобно забывать Суворова и его правила: не ставить себя в положение атакованного, а атаковать самому. Поверьте, на войне энергия молодых людей часто вернее указывает путь, чем вся опытность старых кунктаторов.
– Но в какой же позиции мы атакуем его? Я был на аванпостах нынче, и нельзя решить, где он именно стоит с главными силами, – сказал князь Андрей.
Ему хотелось высказать Долгорукову свой, составленный им, план атаки.
– Ах, это совершенно всё равно, – быстро заговорил Долгоруков, вставая и раскрывая карту на столе. – Все случаи предвидены: ежели он стоит у Брюнна…
И князь Долгоруков быстро и неясно рассказал план флангового движения Вейротера.
Князь Андрей стал возражать и доказывать свой план, который мог быть одинаково хорош с планом Вейротера, но имел тот недостаток, что план Вейротера уже был одобрен. Как только князь Андрей стал доказывать невыгоды того и выгоды своего, князь Долгоруков перестал его слушать и рассеянно смотрел не на карту, а на лицо князя Андрея.
– Впрочем, у Кутузова будет нынче военный совет: вы там можете всё это высказать, – сказал Долгоруков.