P+1 метод Уильямса

(<math>P+1</math>) — метод Уильямса — метод факторизации чисел <math>N \in \mathbb N</math> с помощью последовательностей чисел Люка, разработанный Хью Уильямсом в 1982 году. Алгоритм находит простой делитель <math>p</math> числа <math>n</math>. Аналогичен (<math>P-1</math>) — методу Полларда, но использует разложение на множители числа <math>p+1</math>. Имеет хорошие показатели производительности только в случае, когда <math>p+1</math> легко факторизуется. Как правило, на практике реализуется не часто из-за невысокого процента подобных случаев.

Последовательности чисел Люка

Для дальнейших выкладок нам понадобится ввести последовательности чисел Люка и перечислить некоторые их свойства.

Пусть <math>P</math> и <math>Q</math> — некоторые фиксированные целые числа. Последовательности чисел Люка определяются как:

<math>U_0(P,Q) = 0,\quad U_1(P,Q)=1,\quad U_{n+2}(P,Q)=P\cdot U_{n+1}(P,Q) - Q\cdot U_n(P,Q),n\geq 0</math>

<math>V_0(P,Q) = 2,\quad V_1(P,Q)=P,\quad V_{n+2}(P,Q)=P\cdot V_{n+1}(P,Q) - Q\cdot V_n(P,Q),n\geq 0</math>

Пусть также <math>\Delta = P^2 - 4Q.</math>

Последовательности имеют следующие свойства:

<math> \left\{ \begin{matrix} U_{2n} = V_n \cdot U_n, \\ V_{2n} = V^2_n - 2Q^2_n \end{matrix} \right. \quad(1) </math>

<math> \left\{ \begin{matrix} U_{2n-1} = U^2_n - Q \cdot U^2_{n-1}, \\ V_{2n-1} = V_n \cdot V_{n-1} - P \cdot Q^{n-1}\end{matrix} \right. \quad(2) </math>

<math> \left\{ \begin{matrix} \Delta U_n = P \cdot V_n - 2Q \cdot V_{n-1}, \\ V_n = P \cdot U_n - 2Q \cdot U_{n-1} \end{matrix} \right. \quad(3) </math>

<math> \left\{ \begin{matrix} U_{n+m} = U_m \cdot U_{n+1} - Q \cdot U_{m-1} \cdot U_n, \\ \Delta U_{n+m} = V_m \cdot V_{n+1} - Q \cdot V_{m-1} \cdot V_n \end{matrix} \right. \quad(4) </math>

<math> \left\{ \begin{matrix} U_n(V_k(P, Q), Q^k) = U_{nk}(P,Q)/U_k(P,Q), \\ V_n(V_k(P, Q), Q^k) = V_{nk}(P,Q) \end{matrix} \right. \quad(5) </math>

Для доказательства данных свойств рассмотрим явные формулы последовательности чисел Люка:

<math>U_n(P,Q) = \frac{\alpha^n - \beta^n}{\alpha - \beta} </math>

и

<math>V_n(P,Q) = \alpha^n + \beta^n,</math>

где <math>\alpha</math> и <math>\beta</math> — корни характеристического многочлена

<math>x^2 - P\cdot x + Q</math>

Используя явные формулы и теорему Виетта:

<math>P = \alpha + \beta; \quad Q = \alpha \cdot \beta,</math>

получаем выражения <math>(1), (2), (3), (4) </math> и <math>(5).</math>

Далее выделяем ещё одно свойство:

Если НОД<math>(N, Q) = 1\quad </math> и <math>P^\prime Q\equiv P^2-2Q \mod N,\quad </math> то: <math>P^\prime \equiv \alpha / \beta+\beta / \alpha \quad</math> и <math>Q^\prime \equiv 1, \quad</math> откуда

<math>U_{2m}(P,Q)\equiv P \cdot Q^{m-1}\cdot U_m(P^\prime, 1) \mod N \quad (6)</math>

И, наконец, формулируем теорему:

Если p — нечётное простое число, <math>p \mid Q</math> и символ Лежандра <math>\epsilon = (\Delta/p)</math>, то:

<math> \left\{ \begin{matrix} U_{(p-\epsilon)m}(P,Q) \equiv 0 \mod p, \\ V_{(p-\epsilon)m}(P,Q) \equiv 2Q^{m(1-\epsilon)/2} \mod p \end{matrix} \right. \quad(T1) </math>

Доказательство данной теоремы трудоёмкое, и его можно найти в книге Д. Г. Лемера.

Первый шаг алгоритма

Пусть <math>p</math> — простой делитель факторизуемого числа <math>N</math>, и выполнено разложение:

<math>p+1=\prod^k_{i=1}q_i^{\alpha_i}, </math>

где <math>q_i</math> — простые числа.

Пусть <math>B = \max \{q_i^{\alpha_i} | \forall i: 1 \leq i \leq k\}.</math>

Введём число <math>R=\prod^k_{i=1}q_i^{\beta_i}, </math> где степени <math>\beta_i</math> выбираются таким образом, что <math>q_i^{\beta_i}\leq B, q_i^{\beta_i + 1} > B \quad \forall i: 1 \leq i \leq k. </math>

Тогда <math>p+1 | R.</math>

Далее, согласно теореме <math>(T1),</math> если НОД<math>(N, Q) = 1, (\Delta/p) = -1, </math> то <math>p | U_R(P, Q).</math>

И, следовательно, <math>p | </math> НОД <math>(U_R(P, Q), N),</math> то есть найден делитель искомого числа <math>N</math>.

Стоит обратить внимание, что числа <math>P, Q, p</math> не известны на начальном этапе задачи. Поэтому для упрощения задачи сделаем следующее: так как <math>p | U_R(P, Q),</math> то по свойству (2) <math>p | U_{2R}(P, Q).</math> Далее воспользуемся свойством (6) и получим: <math>p | U_R(P^\prime, 1).</math>

Таким образом, мы без потери общности можем утверждать, что <math>Q=1.</math>

Далее пользуемся теоремой <math>(T1),</math> из которой делаем вывод, что

<math>V_{(p-\epsilon )m}(P,1) \equiv 2 \mod p;</math>

И, следовательно, <math>p | (V_R(P, 1) - 2).</math>

Теперь выбираем некоторое число <math> P </math> такое, что НОД <math>(P^2 - 4, N) = 1;</math>

Обозначаем:

<math>V_n(P)=V_n(P,1), \quad U_n(P) = U_n(P, 1).</math>

Окончательно, нужно найти НОД<math>(V_R(P)-2, N).</math>

Для поиска <math>V_R(P)</math> поступаем следующим образом:

1) раскладываем <math>R</math> в двоичный вид: <math>R=\sum^t_{i=0}b_i2^{t-i}, </math> где <math>b_i=0,1</math>.

2) вводим последовательность натуральных чисел <math>\{f_n\}: f_0 = 1; f_{k+1}=2f_k+b_{k+1}</math>. При этом <math>f_t=R</math>;

3) ищем пары значений <math>(V_{f_{k+1}}, V_{f_{k+1}-1})</math> по следующему правилу:

<math>(V_{f_{k+1}}, V_{f_{k+1}-1})= \left\{ \begin{matrix} (V_{2f_k}, V_{2f_k-1}), when \quad b_{k+1} = 0; \\ (V_{2f_k+1}, V_{2f_k}), when \quad b_{k+1} = 1 \end{matrix} \right.</math>

при этом <math>V_0(P)=2, V_1(P)=P</math>

4) значения <math>V_{2f_k-1}, V_{2f_k}, V_{2f_k+1}</math> ищутся по правилам (которые следуют из свойств <math>(1), (2)</math> и определения последовательности чисел Люка):

<math>\left\{ \begin{matrix} V_{2f-1} \equiv V_fV{f-1}-P \mod N; \\ V_{2f} \equiv V_f^2-2 \mod N; \\ V_{2f+1} \equiv PV_f^2-V_fV_{f-1}-P \mod N \end{matrix} \right.</math>.

Для значений, введённых по умолчанию, то есть <math>N=451889, R=2520, P=6</math> получаем результат:

374468

Делаем проверку этого значения. Для этого считаем НОД<math>(V_R(P)-2, N)=</math> НОД<math>(374468 - 2, 451889)=139</math> и <math>\quad 451889 \vdots 139</math>.

Если мы в первом шаге неудачно выбрали числа <math>R, P</math>, то есть получилось так, что НОД<math>(V_R(P)-2, N)=1</math>, то тогда нужно переходить ко второму шагу. Иначе — работа завершена.

Второй шаг алгоритма

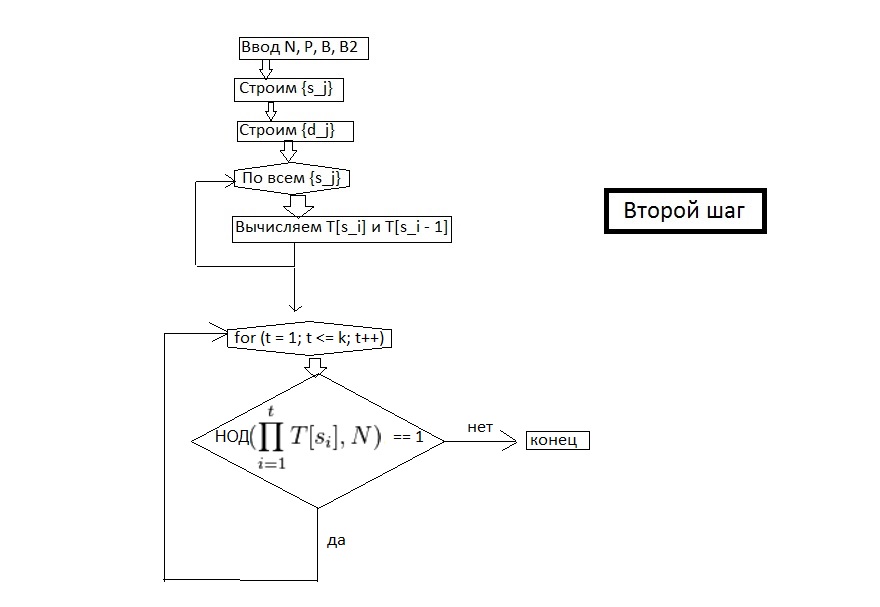Пусть число <math>p+1</math> имеет некоторый простой делитель<math>s</math>, больший чем <math>B</math>, но меньший некоторого <math>B_2</math>, то есть:

<math>p=s \cdot (\prod^k_{i=1}q_i^{\alpha_i})-1</math>, где <math>B < s \leq B_2 </math>

Вводим последовательность простых чисел <math>\{s_j: B < s_j \leq B_2 \quad \forall j = 1, 2, ..., k \}</math>.

Вводим ещё одну последовательность: <math>\{d_j: 2d_j = s_{j+1} - s_j \quad \forall j = 1, 2, ..., k-1 \}</math>

Далее определяем:

<math>T[s_i] \equiv \Delta U_{s_iR}(P)/U_R(P) \mod N</math>.

Используя свойство <math>(5)</math>, получаем первые элементы:

<math>\left\{ \begin{matrix} T[s_1] \equiv PV[s_1] - 2V[s_1-1] \mod N ;\\ T[s_1-1] \equiv 2V[s_1] - PV[s_1-1] \mod N \end{matrix} \right.</math>.

Далее используем свойство <math>(4)</math> и получаем:

<math>\left\{ \begin{matrix} T[s_{i+1}] \equiv T[s_i]U[2d_i+1] - T[s_i-1]U[2d_i]\mod N ,\\ T[s_{i+1}-1] \equiv T[s_i]U[2d_i] - T[s_i-1]U[2d_i-1]\mod N \end{matrix} \right.</math>.

Таким образом, мы вычисляем <math>T[s_i], \forall i=1,2, \ldots, k</math>

Далее считаем:

<math>H_t = </math> НОД<math>(\prod^t_{i=1}T[s_i], N)</math> для <math>t=1,2, \ldots, k</math>

Как только получаем <math>H_t \neq 1 </math>, то прекращаем вычисления.

Для значений, введённых по умолчанию, то есть <math>N=451889, B=10, B_2 = 50, P=7</math> получаем результат:

139,

что является верным ответом.

Сравнение скорости работы

Автором данного метода были проведены тесты <math>p-1</math> и <math>p+1</math> методов на машине AMDAHL 470-V7 на 497 различных числах, которые показали, что в среднем первый шаг алгоритма <math>p+1</math> работает примерно в 2 раза медленнее первого шага алгоритма <math>p-1</math>, а второй шаг — примерно в 4 раза медленнее.

Применение

В связи с тем, что <math>p-1</math>-метод факторизации работает быстрее, <math>p+1</math>-метод применяется на практике очень редко.

Рекорды

На данный момент (14.12.2013) три самых больших простых делителя, найденных методом <math>P+1</math>, состоят из 60, 55 и 53 десятичных цифр.

Кол-во цифр	p	Делитель числа	Найден (кем)	Найден (когда)	B	B2
60	725516237739635905037132916171116034279215026146021770250523	<math>L_{2366}</math>	A. Kruppa P. Montgomery	31.10.2007	<math>10^{11}</math>	<math>10^{15}</math>
55	1273305908528677655311178780176836847652381142062038547	<math>782\cdot6^{782}</math>	P. Leyland	16.05.2011	<math>10^{9}</math>	<math>10^{13}</math>
53	60120920503954047277077441080303862302926649855338567	<math>682\cdot5^{682}</math>	P. Leyland	26.02.2011	<math>10^{8}</math>	<math>10^{12}</math>

Здесь <math>L_{2366}</math> — 2366-й член последовательности чисел Люка.

Литература

• Williams H. C. [www.jstor.org/stable/2007633 A p+1 method of factoring] (англ.) = A p+1 method of factoring // American Mathematical Society. — 1982. — Т. 39, вып. 159. — С. 225-234. — ISSN [www.sigla.ru/table.jsp?f=8&t=3&v0=00255718&f=1003&t=1&v1=&f=4&t=2&v2=&f=21&t=3&v3=&f=1016&t=3&v4=&f=1016&t=3&v5=&bf=4&b=&d=0&ys=&ye=&lng=&ft=&mt=&dt=&vol=&pt=&iss=&ps=&pe=&tr=&tro=&cc=UNION&i=1&v=tagged&s=0&ss=0&st=0&i18n=ru&rlf=&psz=20&bs=20&ce=hJfuypee8JzzufeGmImYYIpZKRJeeOeeWGJIZRrRRrdmtdeee88NJJJJpeeefTJ3peKJJ3UWWPtzzzzzzzzzzzzzzzzzbzzvzzpy5zzjzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzztzzzzzzzbzzzzzzzzzzzzzzzzzzzzzzzzzzzvzzzzzzyeyTjkDnyHzTuueKZePz9decyzzLzzzL*.c8.NzrGJJvufeeeeeJheeyzjeeeeJh*peeeeKJJJJJJJJJJmjHvOJJJJJJJJJfeeeieeeeSJJJJJSJJJ3TeIJJJJ3..E.UEAcyhxD.eeeeeuzzzLJJJJ5.e8JJJheeeeeeeeeeeeyeeK3JJJJJJJJ*s7defeeeeeeeeeeeeeeeeeeeeeeeeeSJJJJJJJJZIJJzzz1..6LJJJJJJtJJZ4....EK*&debug=false 00255718].
• D. H. Lehmer An extended theory of Lucas' functions (англ.) = An extended theory of Lucas' functions // Ann. of Math.. — 1930. — Т. 31, вып. 2. — С. 419-448.
• Ишмухаметов Ш. Т. [old.kpfu.ru/f9/bibl/Monograph_ishm.pdf Методы факторизации натуральных чисел: Учебное пособие]. — Казань: Казанский Университет, 2011. — С. 60-61. — 190 с.

См. также

• Последовательность Люка

Ссылки

• www.mersennewiki.org/index.php/P_Plus_1_Factorization_Method

Отрывок, характеризующий P+1 метод Уильямса

Дело стояло за Наташиной юбкой, которая была слишком длинна; ее подшивали две девушки, обкусывая торопливо нитки. Третья, с булавками в губах и зубах, бегала от графини к Соне; четвертая держала на высоко поднятой руке всё дымковое платье.
– Мавруша, скорее, голубушка!
– Дайте наперсток оттуда, барышня.
– Скоро ли, наконец? – сказал граф, входя из за двери. – Вот вам духи. Перонская уж заждалась.
– Готово, барышня, – говорила горничная, двумя пальцами поднимая подшитое дымковое платье и что то обдувая и потряхивая, высказывая этим жестом сознание воздушности и чистоты того, что она держала.
Наташа стала надевать платье.
– Сейчас, сейчас, не ходи, папа, – крикнула она отцу, отворившему дверь, еще из под дымки юбки, закрывавшей всё ее лицо. Соня захлопнула дверь. Через минуту графа впустили. Он был в синем фраке, чулках и башмаках, надушенный и припомаженный.
– Ах, папа, ты как хорош, прелесть! – сказала Наташа, стоя посреди комнаты и расправляя складки дымки.
– Позвольте, барышня, позвольте, – говорила девушка, стоя на коленях, обдергивая платье и с одной стороны рта на другую переворачивая языком булавки.
– Воля твоя! – с отчаянием в голосе вскрикнула Соня, оглядев платье Наташи, – воля твоя, опять длинно!
Наташа отошла подальше, чтоб осмотреться в трюмо. Платье было длинно.
– Ей Богу, сударыня, ничего не длинно, – сказала Мавруша, ползавшая по полу за барышней.
– Ну длинно, так заметаем, в одну минутую заметаем, – сказала решительная Дуняша, из платочка на груди вынимая иголку и опять на полу принимаясь за работу.
В это время застенчиво, тихими шагами, вошла графиня в своей токе и бархатном платье.
– Уу! моя красавица! – закричал граф, – лучше вас всех!… – Он хотел обнять ее, но она краснея отстранилась, чтоб не измяться.
– Мама, больше на бок току, – проговорила Наташа. – Я переколю, и бросилась вперед, а девушки, подшивавшие, не успевшие за ней броситься, оторвали кусочек дымки.
– Боже мой! Что ж это такое? Я ей Богу не виновата…
– Ничего, заметаю, не видно будет, – говорила Дуняша.
– Красавица, краля то моя! – сказала из за двери вошедшая няня. – А Сонюшка то, ну красавицы!…
В четверть одиннадцатого наконец сели в кареты и поехали. Но еще нужно было заехать к Таврическому саду.
Перонская была уже готова. Несмотря на ее старость и некрасивость, у нее происходило точно то же, что у Ростовых, хотя не с такой торопливостью (для нее это было дело привычное), но также было надушено, вымыто, напудрено старое, некрасивое тело, также старательно промыто за ушами, и даже, и так же, как у Ростовых, старая горничная восторженно любовалась нарядом своей госпожи, когда она в желтом платье с шифром вышла в гостиную. Перонская похвалила туалеты Ростовых.
Ростовы похвалили ее вкус и туалет, и, бережа прически и платья, в одиннадцать часов разместились по каретам и поехали.


Наташа с утра этого дня не имела ни минуты свободы, и ни разу не успела подумать о том, что предстоит ей.
В сыром, холодном воздухе, в тесноте и неполной темноте колыхающейся кареты, она в первый раз живо представила себе то, что ожидает ее там, на бале, в освещенных залах – музыка, цветы, танцы, государь, вся блестящая молодежь Петербурга. То, что ее ожидало, было так прекрасно, что она не верила даже тому, что это будет: так это было несообразно с впечатлением холода, тесноты и темноты кареты. Она поняла всё то, что ее ожидает, только тогда, когда, пройдя по красному сукну подъезда, она вошла в сени, сняла шубу и пошла рядом с Соней впереди матери между цветами по освещенной лестнице. Только тогда она вспомнила, как ей надо было себя держать на бале и постаралась принять ту величественную манеру, которую она считала необходимой для девушки на бале. Но к счастью ее она почувствовала, что глаза ее разбегались: она ничего не видела ясно, пульс ее забил сто раз в минуту, и кровь стала стучать у ее сердца. Она не могла принять той манеры, которая бы сделала ее смешною, и шла, замирая от волнения и стараясь всеми силами только скрыть его. И эта то была та самая манера, которая более всего шла к ней. Впереди и сзади их, так же тихо переговариваясь и так же в бальных платьях, входили гости. Зеркала по лестнице отражали дам в белых, голубых, розовых платьях, с бриллиантами и жемчугами на открытых руках и шеях.
Наташа смотрела в зеркала и в отражении не могла отличить себя от других. Всё смешивалось в одну блестящую процессию. При входе в первую залу, равномерный гул голосов, шагов, приветствий – оглушил Наташу; свет и блеск еще более ослепил ее. Хозяин и хозяйка, уже полчаса стоявшие у входной двери и говорившие одни и те же слова входившим: «charme de vous voir», [в восхищении, что вижу вас,] так же встретили и Ростовых с Перонской.
Две девочки в белых платьях, с одинаковыми розами в черных волосах, одинаково присели, но невольно хозяйка остановила дольше свой взгляд на тоненькой Наташе. Она посмотрела на нее, и ей одной особенно улыбнулась в придачу к своей хозяйской улыбке. Глядя на нее, хозяйка вспомнила, может быть, и свое золотое, невозвратное девичье время, и свой первый бал. Хозяин тоже проводил глазами Наташу и спросил у графа, которая его дочь?
– Charmante! [Очаровательна!] – сказал он, поцеловав кончики своих пальцев.
В зале стояли гости, теснясь у входной двери, ожидая государя. Графиня поместилась в первых рядах этой толпы. Наташа слышала и чувствовала, что несколько голосов спросили про нее и смотрели на нее. Она поняла, что она понравилась тем, которые обратили на нее внимание, и это наблюдение несколько успокоило ее.
«Есть такие же, как и мы, есть и хуже нас» – подумала она.
Перонская называла графине самых значительных лиц, бывших на бале.
– Вот это голландский посланик, видите, седой, – говорила Перонская, указывая на старичка с серебряной сединой курчавых, обильных волос, окруженного дамами, которых он чему то заставлял смеяться.
– А вот она, царица Петербурга, графиня Безухая, – говорила она, указывая на входившую Элен.
– Как хороша! Не уступит Марье Антоновне; смотрите, как за ней увиваются и молодые и старые. И хороша, и умна… Говорят принц… без ума от нее. А вот эти две, хоть и нехороши, да еще больше окружены.
Она указала на проходивших через залу даму с очень некрасивой дочерью.
– Это миллионерка невеста, – сказала Перонская. – А вот и женихи.
– Это брат Безуховой – Анатоль Курагин, – сказала она, указывая на красавца кавалергарда, который прошел мимо их, с высоты поднятой головы через дам глядя куда то. – Как хорош! неправда ли? Говорят, женят его на этой богатой. .И ваш то соusin, Друбецкой, тоже очень увивается. Говорят, миллионы. – Как же, это сам французский посланник, – отвечала она о Коленкуре на вопрос графини, кто это. – Посмотрите, как царь какой нибудь. А всё таки милы, очень милы французы. Нет милей для общества. А вот и она! Нет, всё лучше всех наша Марья то Антоновна! И как просто одета. Прелесть! – А этот то, толстый, в очках, фармазон всемирный, – сказала Перонская, указывая на Безухова. – С женою то его рядом поставьте: то то шут гороховый!
Пьер шел, переваливаясь своим толстым телом, раздвигая толпу, кивая направо и налево так же небрежно и добродушно, как бы он шел по толпе базара. Он продвигался через толпу, очевидно отыскивая кого то.