Частица в периодическом потенциале

В квантовой механике, частица в одномерном периодическом потенциале — это идеализированная задача, которая может быть решена точно (при некоторых специального вида потенциалах), без упрощений. Предполагается, что потенциал бесконечен и периодичен, то есть обладает трансляционной симметрией, что, вообще говоря, не выполняется для реальных кристаллов, и всегда существует как минимум один дефект — поверхность (это приводит к другой задаче о поверхностных состояниях или таммовских уровнях).

Содержание

1 Общий вид спектра
- 1.1 Периодическая задача
- 1.2 Влияние границ
2 Модель Кронига — Пенни
3 Программный код
4 Ссылки
5 См. также

Общий вид спектра

Периодическая задача

Рассмотрим одномерную решётку ионов, расстояние между которыми <math>a</math>. Потенциал при этом будет периодическим. Рассмотрим сначала идеализированный случай бесконечного кристалла. Уравнение Шрёдингера имеет вид:

<math> -\frac{\hbar^2}{2m}\frac{\partial^2 \psi (x)}{\partial x^2} + V_a(x) \psi (x) = E \psi (x)</math>

с периодическим потенциалом <math> V_a(x) = V_a(x+a).</math> Спектр определяется как множество тех энергий, при которых уравнение имеет решения, ограниченные (не стремящиеся к нулю или бесконечности) на всей вещественной оси. Уравнение Шрёдингера имеет второй порядок, соответственно пространство решений является двумерным. Пусть <math>\psi_{1,2}</math> — линейно независимые решения уравнения. Тогда при сдвиге на период, в силу периодичности задачи, они преобразуются через друг друга:

<math>\left( \begin{matrix} \psi_1(x+a) \\ \psi_2(x+a) \end{matrix} \right) = \mathrm{T} \left( \begin{matrix} \psi_1(x) \\ \psi_2(x) \end{matrix} \right)</math>

где <math>\mathrm{T}</math> — некоторая матрица (матрица монодромии). Рассматривая вронскиан, несложно показать, что <math>\mathrm{T}</math> унитарна и <math>\det \mathrm{T} = 1</math>. Отсюда следует, что в некотором базисе она имеет вид

<math>\mathrm{T} = \left( \begin{matrix} e^{\mathrm{i}kx} & 0 \\ 0 & e^{-\mathrm{i}kx} \end{matrix} \right)</math>

Отсюда следует теорема Блоха: соответствующие собственные функции имеют вид

<math> \psi_{1,2} (x) = e^{\mathrm{i}kx} \phi_{1,2}(x), </math>

где <math>\phi_{1,2}(x)</math> — периодические функции. Заметим, что пока что <math>k\in\C</math>. Очевидно, что спектру соответствуют <math>k\in\R</math>, что равносильно (с учётом унитарности) условию на след матрицы монодромии

<math>\mathrm{Tr}\ \mathrm{T} = 2\cos(kx) \in [-2; 2]</math>

Несложно показать, что <math>\mathrm{Tr}( \mathrm{T})(E)</math> есть гладкая функция. Отсюда следует зонная структура спектра: для частицы в периодическом потенциале допустимые уровни энергии — это некоторое, обычно бесконечное, множество отрезков на вещественной оси. Для потенциала общего вида спектр не имеет изолированных точек, при малом шевелении потенциала они либо исчезают, либо превращаются в зоны малой ширины. Заметим, что крайние отрезки спектра в принципе могут быть неограничены, при этом все уровни энергии, начиная с некоторого, являются допустимыми, а полное число зон конечно (см. конечнозонное интегрирование). В подобной постановке задача допускает полное и простое решение в тэта-функциях.

k называют квазиимпульсом, по аналогии с волновой функцией <math>e^{\mathrm{i}kx}</math> для частицы с определённым импульсом k. Как видно, вся волновая функция определяется величиной k и любым участком функции длиной a.

Аналогично возникают энергетические зоны в решётках более высоких размерностей.

Влияние границ

В реальном кристалле число допустимых состояний очень велико. Приводящее к этому дополнительное ограничение на величину квазиимпульса возникает из граничных условий на волновую функцию на поверхности кристалла. При этом вместо непрерывных зон возникают области с плотно расположенными дискретными уровнями энергии (разрешённые зоны) и области, в которых состояний вообще нет (запрещённые зоны). Оценим расстояние между уровнями энергии в разрешённых зонах.

Вместо рассмотрения допустимых уровней энергии (для этого потребовалась бы дополнительная информация, вроде дисперсионного соотношения и точной структуры кристалла) рассмотрим допустимые значения квазиимпульса. При рассмотрении изолированного кристалла обычно рассматриваются периодические граничные условия на волновую функцию. Это предположение оправдано, так как точные граничные условия в реальном кристалле состоят в занулении волновой функции электронов на его границе. Для одномерного кристалла это означает чётность волновой функции (0 находится в центре кристалла). Если же влияние границ на волновую функцию мало́, то приближённо можно забыть про точное значение волновой функции на границе, сохранив лишь свойство симметрии — чётность.

Рассмотрим одномерный кристалл длины <math>L</math>. Граничное условие имеет вид

С учётом теоремы Блоха отсюда следует, что

Таким образом, расстояние между соседними допустимыми значениями квазиимпульса равно

<math>\Delta k = \frac{2\pi n}{L}</math>

Аналогично в общем случае, для кубической решётки:

<math>\Delta k_{x,y,z} = \frac{2\pi n}{ L_{x,y,z} }</math>

Модель Кронига — Пенни

Для упрощения задачи потенциал приближают прямоугольным:

Используя теорему Блоха мы найдём волновую функцию во всём пространстве, но сначала надо найти решение для одного периода, и сделать его гладким на краях, то есть «сшить» значения соседних функций и их производных. Рассмотрим один период потенциала:
У нас есть две независимых области для которых мы найдём решения:

<math>\Rightarrow \psi = A e^{i \alpha x} + A' e^{-i \alpha x} \quad \left( \alpha^2 = {2mE \over \hbar^2} \right)</math>

<math>\Rightarrow \psi = B e^{i \beta x} + B' e^{-i \beta x} \quad \left( \beta^2 = {2m(E+V_0) \over \hbar^2} \right)</math>

Для нахождения u(x) в каждой области нужно проделать следующие преобразования:

<math> \Rightarrow u(0<x<a-b)=A e^{i (\alpha-k) x} + A' e^{-i (\alpha+k) x}</math>

Аналогично получим

Чтобы найти полное решение нам надо убедиться в гладкости искомой функции на границах:

и периодичности u(x) и u'(x)

Эти условия дают следующую матрицу:

<math> \begin{pmatrix} 1 & 1 & -1 & -1 \\ \alpha & -\alpha & -\beta & \beta \\ e^{i(\alpha-k)(a-b)} & e^{-i(\alpha+k)(a-b)} & -e^{-i(\beta-k)b} & -e^{i(\beta+k)b} \\ (\alpha-k)e^{i(\alpha-k)(a-b)} & -(\alpha+k)e^{-i(\alpha+k)(a-b)} & -(\beta-k)e^{-i(\beta-k)b} & (\beta+k)e^{i(\beta+k)b} \end{pmatrix} \begin{pmatrix} A \\ A' \\ B \\ B' \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \\ 0 \end{pmatrix} </math>

Для существования нетривиального решения необходимо зануление детерминанта этой матрицы. После некоторых преобразований получаем:

<math> \cos(k a) = \cos(\beta b) \cos[\alpha(a-b)]-{\alpha^2+\beta^2 \over 2\alpha \beta} \sin(\beta b) \sin[\alpha(a-b)]. \qquad ( * )</math>

Для дальнейшего упрощения мы выполним следующие преобразования, смысл которых заключается в переходе к дельта-образным потенциалам (дираковская гребёнка) :

<math> b \rightarrow 0 \ ; \ V_0 \rightarrow \infty \ ; \ V_0 b = \mathrm{constant}</math>

<math> \Rightarrow \beta b \rightarrow 0 \ ; \ \beta^2 b = \mathrm{constant} \ ; \ \alpha^2 b \rightarrow 0 \ ; \ \sin(\beta b) \rightarrow \beta b \ ; \ \cos(\beta b) \rightarrow 1 </math>

Тогда конечный ответ будет:

<math> \cos(k a) = \cos(\alpha a)-P{\sin(\alpha a) \over \alpha a} \qquad \left( P={\beta^2 a b \over 2} \right) </math>

Программный код

Код для Maple

Следующий программный код написан на языке Maple (9.5). Представляет собой просто графическое решение <math>( * )</math>.

  restart;
  with(plots):
  with(stats[statplots]):
  eq:=cos(k*a)=cos(beta*b)*cos(alpha*(a-b)) - (alpha^2+beta^2)/(2*alpha*beta)*sin(beta*b)*sin(alpha*(a-b));
  alpha:=sqrt(8*Pi^2*m*(E)*e/h^2):
  beta:=sqrt(8*Pi^2*m*(E+V)*e/h^2):
  e:=1.6*1e-19:
  a:=0.54310*1e-9:
  m:=0.19*9.1*1e-31:
  b:=1/5*a:
  h:=6.6*1e-34:
  k(E,V):=arccos(rhs(evalf(eq)))/a;

  #График
  p:=plot({subs(V=10,k(E,V)),subs(V=10,-k(E,V))},E=-5..50,labels=[ka, E],color=blue):
  xyexchange(p);

  #Анимация, зависимость от глубины ямы
  p:=animate( plot, [{k(E,V),-k(E,V)},E=-10..50, color=blue,labels=[ka, E]], V=0..30 ):
  xyexchange(p);

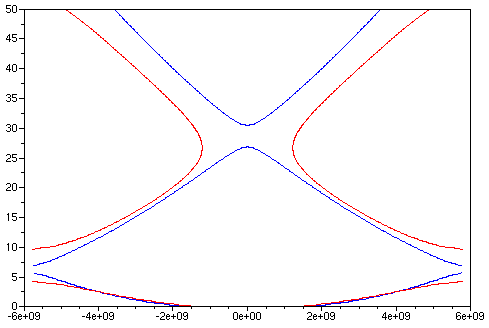
На рисунках представлены графические решения уравнения ( * ).

На правом рисунке видно, как при некотором значении потенциальной энергии возможно образование одномерного бесщелевого полупроводника.

Код для Scilab

Код ниже является фактически переводом предшествующей программы на язык Scilab, за тем исключением, что иллюстрирует также и случай перехода к гребёнке Дирака.

clear all

global Pi e a m b h

Pi = 3.1415926;

step = 0.1;

e = 1.6 * 1e-19;
a = 0.54310 * 1e-9;
m = 0.19*9.1 * 1e-31;
b = 1/5 * a;
h = 6.6 * 1e-34;

function [alpha, beta] = ab(V,E)
  alpha = sqrt(8*Pi^2*m*(E)*e/h^2);
  beta  = sqrt(8*Pi^2*m*(E+V)*e/h^2);
endfunction

function r=kronigpenney(V, E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos((cos(beta*b) .* cos(alpha*(a-b)) ) - (alpha.^2+beta.^2) ./ (2*alpha .* beta) .* sin(beta*b) .* sin(alpha*(a-b)));
endfunction

function r=dirac(V,E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos(cos(alpha * a) - (beta.^2 * b * a) ./ 2 .* sin(alpha*a) ./ (alpha * a));
endfunction

E = [1e-3 : step: 50];

k = kronigpenney(10, E);
plot(k, E, 'b'); plot(-k, E, 'b');

k = dirac(10, E);
plot(k, E, 'r'); plot(-k, E, 'r');

Код для Matlab

Код ниже является переводом предшествующей программы на язык Matlab.

function KronigPenneyM

% clear all
% global Pi e a m b h
Pi = 3.1415926;
step = 0.1;

e = 1.6 * 1e-19;
a = 0.54310 * 1e-9;
m = 0.19*9.1 * 1e-31;
b = 1/5 * a;
h = 6.6 * 1e-34;

E = [0 : step: 50];
N = 3;

hold on; 
k = kronigpenney(N, E);
plot([real(k) NaN, -real(k)], [E NaN E], 'b');

k = dirac(N, E);
plot([real(k) NaN, -real(k)], [E NaN E], 'r');

function [alpha, beta] = ab(V,E)
  alpha = sqrt(8*Pi^2*m*(E)*e/h^2);
  beta  = sqrt(8*Pi^2*m*(E+V)*e/h^2);
end

function r=kronigpenney(V, E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos((cos(beta*b) .* cos(alpha*(a-b)) ) - (alpha.^2+beta.^2) / (2*alpha .* beta) .* sin(beta*b) .* sin(alpha*(a-b)));
end

function r=dirac(V,E)
  [alpha, beta] = ab(V,E);
  r = 1/a * acos(cos(alpha * a) - (beta.^2 * b * a) / 2 .* sin(alpha*a) / (alpha * a));
end
end

Напишите отзыв о статье "Частица в периодическом потенциале"

Ссылки

Задачи по квантовой механике. Часть 1. Галицкий, Карнаков, Коган.
[www.falstad.com/qm1dcrystal/ 1-D periodic potential applet]
[www.mtmi.vu.lt/legacy/pfk/funkc_dariniai/quant_mech/bands.htm Energy band formation]

См. также

Отрывок, характеризующий Частица в периодическом потенциале

На другой день он проснулся поздно. Возобновляя впечатления прошедшего, он вспомнил прежде всего то, что нынче надо представляться императору Францу, вспомнил военного министра, учтивого австрийского флигель адъютанта, Билибина и разговор вчерашнего вечера. Одевшись в полную парадную форму, которой он уже давно не надевал, для поездки во дворец, он, свежий, оживленный и красивый, с подвязанною рукой, вошел в кабинет Билибина. В кабинете находились четыре господина дипломатического корпуса. С князем Ипполитом Курагиным, который был секретарем посольства, Болконский был знаком; с другими его познакомил Билибин.
Господа, бывавшие у Билибина, светские, молодые, богатые и веселые люди, составляли и в Вене и здесь отдельный кружок, который Билибин, бывший главой этого кружка, называл наши, les nфtres. В кружке этом, состоявшем почти исключительно из дипломатов, видимо, были свои, не имеющие ничего общего с войной и политикой, интересы высшего света, отношений к некоторым женщинам и канцелярской стороны службы. Эти господа, повидимому, охотно, как своего (честь, которую они делали немногим), приняли в свой кружок князя Андрея. Из учтивости, и как предмет для вступления в разговор, ему сделали несколько вопросов об армии и сражении, и разговор опять рассыпался на непоследовательные, веселые шутки и пересуды.
– Но особенно хорошо, – говорил один, рассказывая неудачу товарища дипломата, – особенно хорошо то, что канцлер прямо сказал ему, что назначение его в Лондон есть повышение, и чтоб он так и смотрел на это. Видите вы его фигуру при этом?…
– Но что всего хуже, господа, я вам выдаю Курагина: человек в несчастии, и этим то пользуется этот Дон Жуан, этот ужасный человек!
Князь Ипполит лежал в вольтеровском кресле, положив ноги через ручку. Он засмеялся.
– Parlez moi de ca, [Ну ка, ну ка,] – сказал он.
– О, Дон Жуан! О, змея! – послышались голоса.
– Вы не знаете, Болконский, – обратился Билибин к князю Андрею, – что все ужасы французской армии (я чуть было не сказал – русской армии) – ничто в сравнении с тем, что наделал между женщинами этот человек.
– La femme est la compagne de l'homme, [Женщина – подруга мужчины,] – произнес князь Ипполит и стал смотреть в лорнет на свои поднятые ноги.
Билибин и наши расхохотались, глядя в глаза Ипполиту. Князь Андрей видел, что этот Ипполит, которого он (должно было признаться) почти ревновал к своей жене, был шутом в этом обществе.
– Нет, я должен вас угостить Курагиным, – сказал Билибин тихо Болконскому. – Он прелестен, когда рассуждает о политике, надо видеть эту важность.
Он подсел к Ипполиту и, собрав на лбу свои складки, завел с ним разговор о политике. Князь Андрей и другие обступили обоих.
– Le cabinet de Berlin ne peut pas exprimer un sentiment d'alliance, – начал Ипполит, значительно оглядывая всех, – sans exprimer… comme dans sa derieniere note… vous comprenez… vous comprenez… et puis si sa Majeste l'Empereur ne deroge pas au principe de notre alliance… [Берлинский кабинет не может выразить свое мнение о союзе, не выражая… как в своей последней ноте… вы понимаете… вы понимаете… впрочем, если его величество император не изменит сущности нашего союза…]
– Attendez, je n'ai pas fini… – сказал он князю Андрею, хватая его за руку. – Je suppose que l'intervention sera plus forte que la non intervention. Et… – Он помолчал. – On ne pourra pas imputer a la fin de non recevoir notre depeche du 28 novembre. Voila comment tout cela finira. [Подождите, я не кончил. Я думаю, что вмешательство будет прочнее чем невмешательство И… Невозможно считать дело оконченным непринятием нашей депеши от 28 ноября. Чем то всё это кончится.]
И он отпустил руку Болконского, показывая тем, что теперь он совсем кончил.
– Demosthenes, je te reconnais au caillou que tu as cache dans ta bouche d'or! [Демосфен, я узнаю тебя по камешку, который ты скрываешь в своих золотых устах!] – сказал Билибин, y которого шапка волос подвинулась на голове от удовольствия.
Все засмеялись. Ипполит смеялся громче всех. Он, видимо, страдал, задыхался, но не мог удержаться от дикого смеха, растягивающего его всегда неподвижное лицо.
– Ну вот что, господа, – сказал Билибин, – Болконский мой гость в доме и здесь в Брюнне, и я хочу его угостить, сколько могу, всеми радостями здешней жизни. Ежели бы мы были в Брюнне, это было бы легко; но здесь, dans ce vilain trou morave [в этой скверной моравской дыре], это труднее, и я прошу у всех вас помощи. Il faut lui faire les honneurs de Brunn. [Надо ему показать Брюнн.] Вы возьмите на себя театр, я – общество, вы, Ипполит, разумеется, – женщин.
– Надо ему показать Амели, прелесть! – сказал один из наших, целуя кончики пальцев.
– Вообще этого кровожадного солдата, – сказал Билибин, – надо обратить к более человеколюбивым взглядам.
– Едва ли я воспользуюсь вашим гостеприимством, господа, и теперь мне пора ехать, – взглядывая на часы, сказал Болконский.
– Куда?
– К императору.
– О! о! о!
– Ну, до свидания, Болконский! До свидания, князь; приезжайте же обедать раньше, – пocлшaлиcь голоса. – Мы беремся за вас.
– Старайтесь как можно более расхваливать порядок в доставлении провианта и маршрутов, когда будете говорить с императором, – сказал Билибин, провожая до передней Болконского.
– И желал бы хвалить, но не могу, сколько знаю, – улыбаясь отвечал Болконский.
– Ну, вообще как можно больше говорите. Его страсть – аудиенции; а говорить сам он не любит и не умеет, как увидите.

На выходе император Франц только пристально вгляделся в лицо князя Андрея, стоявшего в назначенном месте между австрийскими офицерами, и кивнул ему своей длинной головой. Но после выхода вчерашний флигель адъютант с учтивостью передал Болконскому желание императора дать ему аудиенцию.
Император Франц принял его, стоя посредине комнаты. Перед тем как начинать разговор, князя Андрея поразило то, что император как будто смешался, не зная, что сказать, и покраснел.
– Скажите, когда началось сражение? – спросил он поспешно.
Князь Андрей отвечал. После этого вопроса следовали другие, столь же простые вопросы: «здоров ли Кутузов? как давно выехал он из Кремса?» и т. п. Император говорил с таким выражением, как будто вся цель его состояла только в том, чтобы сделать известное количество вопросов. Ответы же на эти вопросы, как было слишком очевидно, не могли интересовать его.
– В котором часу началось сражение? – спросил император.
– Не могу донести вашему величеству, в котором часу началось сражение с фронта, но в Дюренштейне, где я находился, войско начало атаку в 6 часу вечера, – сказал Болконский, оживляясь и при этом случае предполагая, что ему удастся представить уже готовое в его голове правдивое описание всего того, что он знал и видел.
Но император улыбнулся и перебил его:
– Сколько миль?
– Откуда и докуда, ваше величество?
– От Дюренштейна до Кремса?
– Три с половиною мили, ваше величество.
– Французы оставили левый берег?
– Как доносили лазутчики, в ночь на плотах переправились последние.
– Достаточно ли фуража в Кремсе?
– Фураж не был доставлен в том количестве…
Император перебил его.
– В котором часу убит генерал Шмит?…
– В семь часов, кажется.
– В 7 часов. Очень печально! Очень печально!
Император сказал, что он благодарит, и поклонился. Князь Андрей вышел и тотчас же со всех сторон был окружен придворными. Со всех сторон глядели на него ласковые глаза и слышались ласковые слова. Вчерашний флигель адъютант делал ему упреки, зачем он не остановился во дворце, и предлагал ему свой дом. Военный министр подошел, поздравляя его с орденом Марии Терезии З й степени, которым жаловал его император. Камергер императрицы приглашал его к ее величеству. Эрцгерцогиня тоже желала его видеть. Он не знал, кому отвечать, и несколько секунд собирался с мыслями. Русский посланник взял его за плечо, отвел к окну и стал говорить с ним.
Вопреки словам Билибина, известие, привезенное им, было принято радостно. Назначено было благодарственное молебствие. Кутузов был награжден Марией Терезией большого креста, и вся армия получила награды. Болконский получал приглашения со всех сторон и всё утро должен был делать визиты главным сановникам Австрии. Окончив свои визиты в пятом часу вечера, мысленно сочиняя письмо отцу о сражении и о своей поездке в Брюнн, князь Андрей возвращался домой к Билибину. У крыльца дома, занимаемого Билибиным, стояла до половины уложенная вещами бричка, и Франц, слуга Билибина, с трудом таща чемодан, вышел из двери.
Прежде чем ехать к Билибину, князь Андрей поехал в книжную лавку запастись на поход книгами и засиделся в лавке.
– Что такое? – спросил Болконский.
– Ach, Erlaucht? – сказал Франц, с трудом взваливая чемодан в бричку. – Wir ziehen noch weiter. Der Bosewicht ist schon wieder hinter uns her! [Ах, ваше сиятельство! Мы отправляемся еще далее. Злодей уж опять за нами по пятам.]
– Что такое? Что? – спрашивал князь Андрей.
Билибин вышел навстречу Болконскому. На всегда спокойном лице Билибина было волнение.