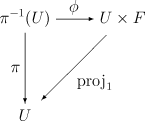Локально тривиальное расслоение

Локально тривиальное расслоение — расслоение, которое локально выглядит как прямое произведение.

Определение

Пусть <math>E</math>, <math>B</math> и <math>F</math> суть топологические пространства. Сюрьективное отображение <math>\pi \colon E\to B</math> называется локально тривиальным расслоением пространства <math>E</math> над базой <math>B</math> со слоем <math>F</math>  если для всякой точки базы <math>x\in B</math> существует окрестность <math>U \sub B</math>, над которой расслоение тривиально. Последнее означает, что существует гомеоморфизм <math>\phi\colon \pi^{-1}(U)\to U\times F</math>, такой что коммутативна диаграмма

.

Здесь <math>\mathrm{proj_1}:\, U\times F \to U</math> — проекция произведения пространств на первый сомножитель.

Пространство <math>E</math> также называется тотальным пространством расслоения или расслоенным пространством.

Связанные определения

• Сечение расслоения — это отображение <math>s: B \to E</math>, такое что <math>\pi \circ s = \mathrm{id}_B</math>. Вообще говоря, не каждое расслоение имеет сечение. Например, пусть <math>M</math> — многообразие, а <math>E \to M</math> — подрасслоение векторов единичной длины в касательном расслоении <math>TM</math>. Тогда сечение расслоения <math>E</math> — это векторное поле без нулей на <math>M</math>. Теорема о причёсывании ежа показывает, что на сфере такого поля не существует.
• Множество <math>F_x = \pi^{-1}\{x\}</math> называется слоем расслоения <math>\pi</math> над точкой <math>x\in B</math>. Каждый слой гомеоморфен пространству <math>F</math>, поэтому пространство <math>F</math> называется общим (или модельным) слоем расслоения <math>\pi</math>,
• Гомеоморфизм <math>\varphi</math>, отождествляющий ограничение расслоения <math>\pi</math> над окрестностью точки <math>x</math> с некоторым тривиальным расслоением, называется локальной тривиализацией расслоения <math>\pi</math> над окрестностью точки <math>x</math>.
• Если <math>\{U_{\alpha}\}</math> — покрытие базы <math>B</math> открытыми множествами, и <math>\varphi_{\alpha}:\pi^{-1}(U_{\alpha}) \to U_{\alpha}\times F</math> — соответствующие им отображения тривиализации, тогда семейство <math>\{(U_{\alpha}, \varphi_{\alpha})\}</math> называется тривиализующим атласом расслоения <math>\pi:E\to B</math>.
• Предположим локально тривиальное расслоение <math>\pi:E\to B</math> снабжено покрытием <math>\{U_\alpha\}</math> базы <math>B</math> с выделенной тривиализацией <math>\phi_\alpha : U_\alpha\times F\to \pi^{-1}(U_\alpha)</math> и сужение любого отображения сличения <math>\phi_\alpha^{-1}\circ\phi_\beta</math> на слой принадлежит некоторой подгруппе <math>G</math> группы всех автоморфизмов <math>F</math>. Тогда <math>\pi</math> называется локально тривиальным расслоением со структурной группой <math>G</math>.

Примеры

• Тривиальное расслоение, то есть проекция <math>B\times F\to B</math> на первый сомножитель.
• Любое накрытие является локально тривиальным расслоением с дискретным слоем.
• Касательное, кокасательное и тензорные расслоения над произвольным многообразием локально тривиальны.
• Если на пространстве <math>E</math> задано непрерывное свободное действие группы <math>G</math>, то естественное отображение <math>E\to E/G</math> является локально тривиальным расслоением. Расслоения такого типа называются главными.
• Лист Мёбиуса — пространство нетривиального расслоения над окружностью.
• Расслоение Хопфа — это нетривиальное расслоение <math>S^3 \to S^2=S^3/S^1</math>. Оно не имеет сечений, так как оно является главным расслоением со структурной группой <math>U(1)</math>, а любое главное расслоение, допускающее сечение, тривиально.
• Сконструировать расслоение можно, задав произвольно его базу (пространство <math>B</math>), общий слой (пространство <math>F</math>) и отображения перехода (1-коцикл Чеха <math>\{u_{\alpha\beta}: U_{\alpha}\to \mathrm{Aut}\, F\}</math>) для какого-нибудь открытого покрытия пространства <math>B</math>. Тогда пространство E формально можно получить как множество троек вида <math>\{(\alpha, x, f_{\alpha}):\,x\in U_{\alpha},\, f_{\alpha}\in F\}</math> с правилом отождествления:

<math>(\alpha, x, f_{\alpha}) = (\beta, x, f_{\beta})</math>, если <math>f_{\beta} = u_{\beta\alpha}f_{\alpha}</math>

Свойства

• Для локально тривиальных расслоений верна теорема о накрывающей гомотопии. Пусть заданы <math>\pi: E\to B</math> — локально тривиальное расслоение, отображения <math>g\colon M\to B</math> и <math>f\colon M \to E</math>, так что <math>g = \pi \circ f</math>, и гомотопия <math>\tilde g\colon M\times [0;1] \to B</math> отображения <math>g</math> (<math>\tilde g(m,0) = g(m)</math>). Тогда существует гомотопия <math>\tilde f\colon M\times [0;1] \to E</math> отображения <math>f</math>, такая что диаграмма коммутативна

<math>\begin{matrix}

M\times [0;1] \! && \stackrel{\tilde f}{\longrightarrow} \! && E \\ \\

 && \tilde g \searrow  && \downarrow \pi \\

\\

 &&  && B

\end{matrix}</math>

• Пусть имеется локально тривиальное расслоение <math>E\to B</math> со слоем <math>F</math> (иногда записываемое формально как <math>F\to E \to B</math>). Тогда последовательность гомотопических групп точна:

<math>\dots \to \pi_2(F) \to \pi_2(E) \to \pi_2(B) \to \pi_1(F) \to \pi_1(E) \to \pi_1(B) \to \pi_0(F)</math>

• Отображения перехода удовлетворяют условию 1-коцикла Чеха:

Если <math>x\in U_{\alpha}\cap U_{\beta}\cap U_{\gamma}</math>, то <math>u_{\beta\alpha}(x) = u_{\beta\gamma}(x)\circ u_{\gamma\alpha}(x)</math>.

• Два расслоения над одной и той же базой и с одним и тем же общим слоем изоморфны тогда и только тогда, когда 1-коциклы Чеха, соответствующие им, когомологичны. (Отметим, что в случае, когда группа <math>\mathrm{Aut}\, F</math> некоммутативна, одномерные когомологии <math>H^1(B,\mathrm{Aut}\, F)</math> не образуют группу, а образуют множество, на котором действует (слева) группа 0-коцепей Чеха <math>C^0(B,\mathrm{Aut}\, F)</math>:

  <math>u_{\alpha\beta}'(x) = f_{\alpha}(x)\circ u_{\alpha\beta}(x) \circ f_{\beta}(x)^{-1}</math>,

где <math>\{f_{\alpha}: U_{\alpha}\to \mathrm{Aut}\, F\}</math> — 0-коцепь Чеха, действующая на 1-коцикл Чеха <math>\{u_{\alpha\beta}: U_{\alpha}\cap U_{\beta}\to \mathrm{Aut}\, F\}</math>. 1-коциклы называются когомологичными, если они лежат в одной орбите этого действия.)

• Для любого локально тривиального расслоения <math>\pi:X\to B</math> и непрерывного отображения <math>f:B'\to B</math> индуцированное расслоение <math>f^*(\pi)</math> является локально тривиальным.

Вариации и обобщения

• Локально тривиальные расслоения являются частным случаем
  • расслоений Гуревича и
  • расслоений Серра.

• Если пространства <math>E, B, F</math> — гладкие (дифференцируемые) многообразия, отображение <math>\pi</math> — гладкое и допускающее тривиализующий атлас с гладкими отображениями тривиализации, то само расслоение называется гладким расслоением.
• Расслоение называется голоморфным, если пространства <math>E, B, F</math> — комплексные многообразия, отображение <math>\pi</math> — голоморфное и существует тривиализующий атлас с голоморфными отображениями тривиализации.
• Главное расслоение.

См. Также

• Теория Янга — Миллса

Литература

• Васильев В. А. Введение в топологию. — М.: ФАЗИС, 1997. — 132 с. — ISBN 5-7036-0036-7.