Непрерывная функция
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
Определения
ε-δ определение
Пусть <math>D\subset\R</math> и <math>f: D\to\R</math>.
Функция <math>f</math> непрерывна в точке <math>x_0\in D</math>, если для любого <math>\varepsilon>0</math> существует <math>\delta>0</math> такое, что для любого
- <math>x\in D,\ |x-x_0|<\delta \Rightarrow |f(x)-f(x_0)|<\varepsilon.</math>
Функция <math>f</math> непрерывна на множестве <math>E</math>, если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция <math>f</math> класса <math>C^0</math> и пишут: <math>f\in C^0(E)</math> или, подробнее, <math>f\in C^0(E, \mathbb{R})</math>.
Комментарии
- Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция <math>f</math> непрерывна в точке <math>x_0</math>, предельной для множества <math>D</math>, если <math>f</math> имеет предел в точке <math>x_0</math>, и этот предел совпадает со значением функции <math>f(x_0)</math>.
- По сравнению с определением предела функции по Коши в определении непрерывности нет требования, обязывающего все значения аргумента <math>x</math> удовлетворять условию <math>0 < \left\vert x - a \right\vert</math>, т.е. быть отличными от а.
- Функция непрерывна в точке, если её колебание в данной точке равно нулю.
Точки разрыва
Если условие, входящее в определение непрерывности функции, в некоторой точке нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если <math>A</math> — значение функции <math>f</math> в точке <math>a</math>, то предел такой функции (если он существует) не совпадает с <math>A</math>. На языке окрестностей условие разрывности функции <math>f</math> в точке <math>a</math> получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки <math>A</math> области значений функции <math>f</math>, что как бы мы близко не подходили к точке <math>a</math> области определения функции <math>f</math>, всегда найдутся такие точки, чьи образы будут за пределами окрестности точки <math>A</math>.
Классификация точек разрыва в R¹
Классификация разрывов функций <math>f: X \to Y</math> зависит от того, как устроены множества X и Y. Здесь приведена классификация для простейшего случая — <math>f: \mathbb{R} \to \mathbb{R}</math>. Таким же образом классифицируют и особые точки (точки, где функция не определена). Стоит заметить, что классификация в <math>\mathbb{R}</math> различается от автора к автору.
Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
- если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода. К точкам разрыва первого рода относят устранимые разрывы и скачки.
- если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода. К точкам разрыва второго рода относят полюса и точки существенного разрыва.
|
Устранимая точка разрыва
Если предел функции существует и конечен, но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
- <math>\lim\limits_{x\to a} f(x) \neq f(a)</math>,
то точка <math>a</math> называется точкой устранимого разрыва функции <math>f</math> (в комплексном анализе — устранимая особая точка).
Если «поправить» функцию <math>f</math> в точке устранимого разрыва и положить <math>f(a) = \lim\limits_{x\to a} f(x)</math>, то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.
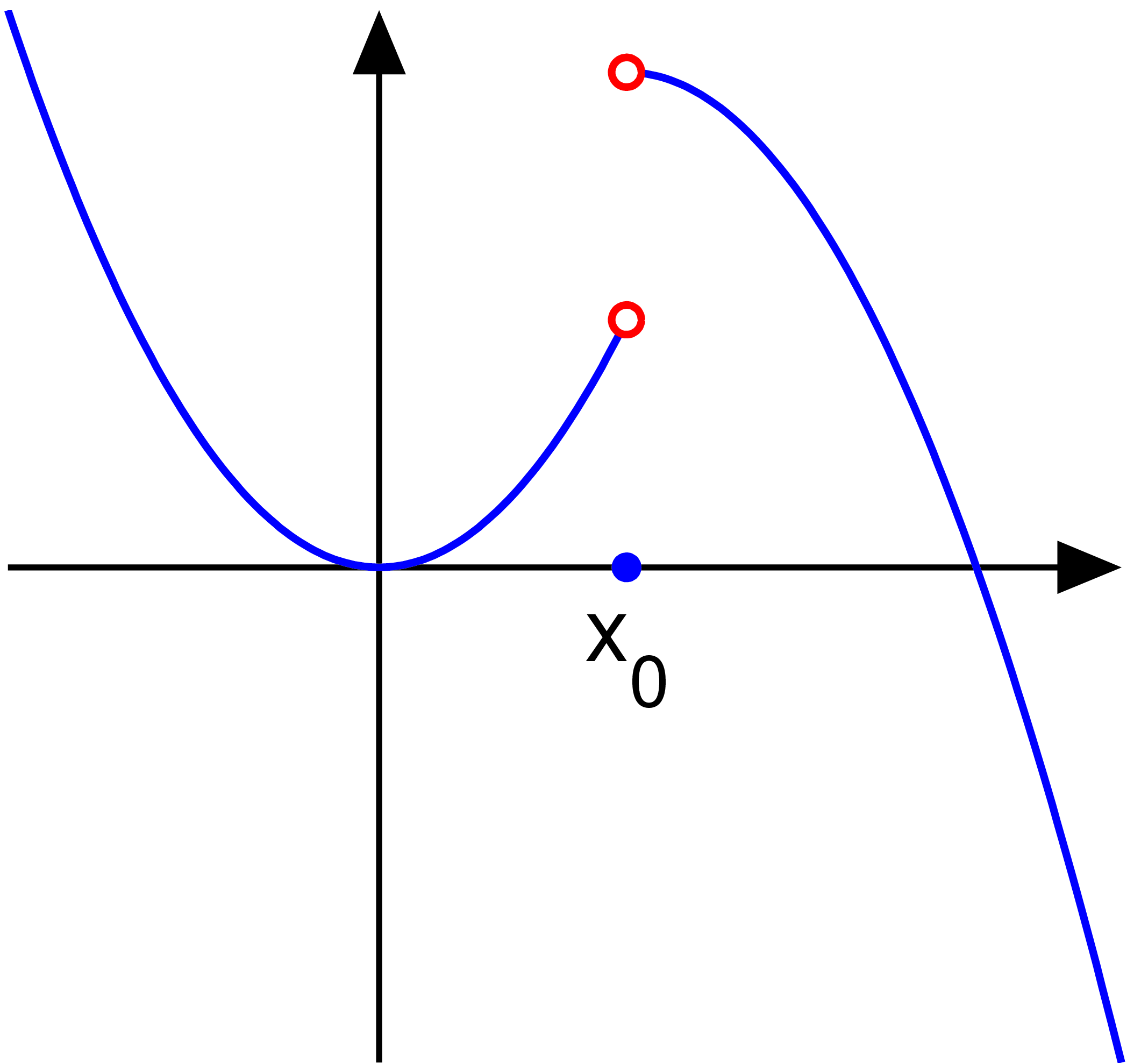
Точка разрыва «скачок»
Разрыв «скачок» возникает, если
- <math>\lim\limits_{x\to a-0} f(x) \neq \lim\limits_{x\to a+0} f(x)</math>.
Точка разрыва «полюс»
Разрыв «полюс» возникает, если один из односторонних пределов бесконечен.
- <math>\lim\limits_{x\to a-0} f(x) = \pm \infty</math> или <math>\lim\limits_{x\to a+0} f(x) = \pm \infty</math>.
Точка существенного разрыва
В точке существенного разрыва один из односторонних пределов вообще отсутствует.
Классификация изолированных особых точек в Rn, n>1
Для функций <math>f: \mathbb{R}^n \to \mathbb{R}^n</math> и <math>f: \mathbb{C} \to \mathbb{C}</math> нет нужды работать с точками разрыва, зато часто приходится работать с особыми точками (точками, где функция не определена). Классификация сходная.
- Если <math>\exists \lim\limits_{x\to a} f(x)</math>, то это устранимая особая точка (аналогично функции действительного аргумента).
- Полюс определяется как <math>\lim\limits_{x\to a} f(x) = \infty</math>. В многомерных пространствах, если модуль числа растёт, считается, что <math>f(x) \to \infty</math>, каким путём бы он ни рос.
- Если предел вообще не существует, это существенная особая точка.
Понятие «скачок» отсутствует. То, что в <math>\mathbb{R}</math> считается скачком, в пространствах бóльших размерностей — существенная особая точка.
Свойства
Локальные
- Функция, непрерывная в точке <math>a</math>, является ограниченной в некоторой окрестности этой точки.
- Если функция <math>f</math> непрерывна в точке <math>a</math> и <math>f(a)>0</math> (или <math>f(a)<0</math>), то <math>f(x)>0</math> (или <math>f(x)<0</math>) для всех <math>x</math>, достаточно близких к <math>a</math>.
- Если функции <math>f</math> и <math>g</math> непрерывны в точке <math>a</math>, то функции <math>f+g</math> и <math>f \cdot g</math> тоже непрерывны в точке <math>a</math>.
- Если функции <math>f</math> и <math>g</math> непрерывны в точке <math>a</math> и при этом <math>g(a)\neq 0</math>, то функция <math>f/g</math> тоже непрерывна в точке <math>a</math>.
- Если функция <math>f</math> непрерывна в точке <math>a</math> и функция <math>g</math> непрерывна в точке <math>b=f(a)</math>, то их композиция <math>h=g\circ f</math> непрерывна в точке <math>a</math>.
Глобальные
- Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
- Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
- Областью значений функции <math>f</math>, непрерывной на отрезке <math>[a,b]</math>, является отрезок <math>[\min f, \ \max f],</math> где минимум и максимум берутся по отрезку <math>[a,b]</math>.
- Если функция <math>f</math> непрерывна на отрезке <math>[a,b]</math> и <math>f(a)\cdot f(b)<0,</math> то существует точка <math>\xi \in (a,b),</math> в которой <math>f(\xi)=0</math>.
- Если функция <math>f</math> непрерывна на отрезке <math>[a,b]</math> и число <math>\varphi</math> удовлетворяет неравенству <math>f(a)< \varphi < f(b)</math> или неравенству <math>f(a)> \varphi > f(b),</math> то существует точка <math>\xi \in (a,b),</math> в которой <math>f(\xi)=\varphi</math>.
- Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
- Монотонная функция на отрезке <math>[a,b]</math> непрерывна в том и только в том случае, когда область её значений является отрезком с концами <math>f(a)</math> и <math>f(b)</math>.
- Если функции <math>f</math> и <math>g</math> непрерывны на отрезке <math>[a,b]</math>, причем <math>f(a)< g(a)</math> и <math>f(b) > g(b),</math> то существует точка <math>\xi \in (a,b),</math> в которой <math>f(\xi)=g(\xi).</math> Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Примеры
Элементарные функции
Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.
Функция с устранимым разрывом
Функция <math>f\colon\mathbb{R} \to \mathbb{R},</math> задаваемая формулой
- <math>f(x) = \begin{cases}
\frac{\sin x}{x}, & x \neq 0 \\ 0, & x = 0 \end{cases}</math>
непрерывна в любой точке <math>x \neq 0.</math> Точка <math>x=0</math> является точкой устранимого разрыва, ибо предел функции
- <math>\lim\limits_{x \to 0} f(x) = \lim\limits_{x \to 0} \frac{\sin x}{x} = 1 \neq f(0).</math>
Функция знака
Функция
- <math>f(x) = \sgn x = \begin{cases}
-1, & x < 0 \\ 0, & x = 0 \\ 1, & x > 0 \end{cases},\quad x\in \R</math>
называется функцией знака.
Эта функция непрерывна в каждой точке <math>x \neq 0</math>.
Точка <math>x=0</math> является точкой разрыва первого рода, причём
- <math>\lim\limits_{x \to 0-}f(x) = -1 \neq 1 = \lim\limits_{x \to 0+}f(x)</math>,
в то время как в самой точке функция обращается в нуль.
Ступенчатая функция
Ступенчатая функция, определяемая как
- <math>f(x) = \begin{cases}
1,& x \geqslant 0\\ 0, & x < 0 \end{cases},\quad x\in \mathbb{R}</math> является всюду непрерывной, кроме точки <math>x=0</math>, где функция терпит разрыв первого рода. Тем не менее, в точке <math>x=0</math> существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, данная функция является примером непрерывной справа функции на всей области определения.
Аналогично, ступенчатая функция, определяемая как
- <math>f(x) = \begin{cases}
1,& x > 0\\ 0, & x \leqslant 0 \end{cases},\quad x\in \mathbb{R}</math>
является примером непрерывной слева функции на всей области определения.
Функция Дирихле
Функция
- <math>f(x) = \begin{cases}
1,& x \in \mathbb{Q}\\ 0, & x \in \mathbb{R}\setminus\mathbb{Q} \end{cases}</math> называется функцией Дирихле. По сути, функция Дирихле — это характеристическая функция множества рациональных чисел. Эта функция является всюду разрывной функцией, поскольку на каждом интервале существуют как рациональные, так и иррациональные числа.
Функция Римана
Функция
- <math>f(x) = \begin{cases}
\frac{1}{n},& x=\frac{m}{n}\in \mathbb{Q},\ (m,n)=1\\ 0, & x \in \mathbb{R}\setminus\mathbb{Q} \end{cases}</math> называется функцией Римана или функцией Томае (англ.).
Эта функция является непрерывной всюду в множестве иррациональных чисел (<math>\mathbb{R}\setminus\mathbb{Q}</math>), поскольку предел функции в каждой точке равен нулю.
Вариации и обобщения
Равномерная непрерывность
Функция <math>f</math> называется равномерно непрерывной на <math>E</math>, если для любого <math>\varepsilon>0</math> существует <math>\delta>0</math> такое, что для любых двух точек <math>x_1</math> и <math>x_2</math> таких, что <math>|x_1-x_2|<\delta</math>, выполняется <math>|f(x_1)-f(x_2)|<\varepsilon</math>.
Каждая равномерно непрерывная на множестве <math>E</math> функция, очевидно, является также и непрерывной на нём. Обратное, вообще говоря, неверно. Однако, если область определения — компакт, то непрерывная функция оказывается также и равномерно непрерывной на данном отрезке.
Полунепрерывность
Существует два симметричных друг другу свойства — полунепрерывность снизу и полунепрерывность сверху:
- функция <math>f</math> называется полунепрерывной снизу в точке <math>a</math>, если для любого <math>\varepsilon>0</math> существует такая окрестность <math>U_E(a)</math>, что <math>f(x)>f(a)-\varepsilon</math> для всякого <math>x\in U_E(a)</math>;
- функция <math>f</math> называется полунепрерывной сверху в точке <math>a</math>, если для любого <math>\varepsilon>0</math> существует такая окрестность <math>U_E(a)</math>, что <math>f(x)<f(a)+\varepsilon</math> для всякого <math>x\in U_E(a)</math>.
Между непрерывностью и полунепрерывностью имеется следующая связь:
- если взять функцию <math>f</math>, непрерывную в точке <math>a</math>, и уменьшить значение <math>f(a)</math> (на конечную величину), то мы получим функцию, полунепрерывную снизу в точке <math>a</math>;
- если взять функцию <math>f</math>, непрерывную в точке <math>a</math>, и увеличить значение <math>f(a)</math> (на конечную величину), то мы получим функцию, полунепрерывную сверху в точке <math>a</math>.
В соответствии с этим можно допустить для полунепрерывных функций бесконечные значения:
- если <math>f(a)=-\infty</math>, то будем считать такую функцию полунепрерывной снизу в точке <math>a</math>;
- если <math>f(a)=+\infty</math>, то будем считать такую функцию полунепрерывной сверху в точке <math>a</math>.
Односторонняя непрерывность
Функция <math>f</math> называется односторонне непрерывной слева (справа) в каждой точке <math>x_0</math> её области определения, если для одностороннего предела выполняется равенство: <math>f(x_0)=\lim\limits_{x\to x_0-} f(x)</math> <math>(f(x_0)=\lim\limits_{x\to x_0+} f(x)).</math>
Непрерывность почти всюду
На вещественной прямой обычно рассматривается простая линейная мера Лебега. Если функция <math>f</math> такова, что она непрерывна всюду на <math>E</math>, кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
В том случае, когда множество точек разрыва функции не более чем счётно, мы получаем класс интегрируемых по Риману функций (см. критерий интегрируемости функции по Риману).
Напишите отзыв о статье "Непрерывная функция"
Литература
- Зорич В. А. Математический анализ, часть I. — М.: Физматлит, 1984. — 544 с.
Отрывок, характеризующий Непрерывная функция
Охотник, стоявший в яме, тронулся и выпустил собак, и Николай увидал красную, низкую, странную лисицу, которая, распушив трубу, торопливо неслась по зеленям. Собаки стали спеть к ней. Вот приблизились, вот кругами стала вилять лисица между ними, всё чаще и чаще делая эти круги и обводя вокруг себя пушистой трубой (хвостом); и вот налетела чья то белая собака, и вслед за ней черная, и всё смешалось, и звездой, врозь расставив зады, чуть колеблясь, стали собаки. К собакам подскакали два охотника: один в красной шапке, другой, чужой, в зеленом кафтане.«Что это такое? подумал Николай. Откуда взялся этот охотник? Это не дядюшкин».
Охотники отбили лисицу и долго, не тороча, стояли пешие. Около них на чумбурах стояли лошади с своими выступами седел и лежали собаки. Охотники махали руками и что то делали с лисицей. Оттуда же раздался звук рога – условленный сигнал драки.
– Это Илагинский охотник что то с нашим Иваном бунтует, – сказал стремянный Николая.
Николай послал стремяного подозвать к себе сестру и Петю и шагом поехал к тому месту, где доезжачие собирали гончих. Несколько охотников поскакало к месту драки.
Николай слез с лошади, остановился подле гончих с подъехавшими Наташей и Петей, ожидая сведений о том, чем кончится дело. Из за опушки выехал дравшийся охотник с лисицей в тороках и подъехал к молодому барину. Он издалека снял шапку и старался говорить почтительно; но он был бледен, задыхался, и лицо его было злобно. Один глаз был у него подбит, но он вероятно и не знал этого.
– Что у вас там было? – спросил Николай.
– Как же, из под наших гончих он травить будет! Да и сука то моя мышастая поймала. Поди, судись! За лисицу хватает! Я его лисицей ну катать. Вот она, в тороках. А этого хочешь?… – говорил охотник, указывая на кинжал и вероятно воображая, что он всё еще говорит с своим врагом.
Николай, не разговаривая с охотником, попросил сестру и Петю подождать его и поехал на то место, где была эта враждебная, Илагинская охота.
Охотник победитель въехал в толпу охотников и там, окруженный сочувствующими любопытными, рассказывал свой подвиг.
Дело было в том, что Илагин, с которым Ростовы были в ссоре и процессе, охотился в местах, по обычаю принадлежавших Ростовым, и теперь как будто нарочно велел подъехать к острову, где охотились Ростовы, и позволил травить своему охотнику из под чужих гончих.
Николай никогда не видал Илагина, но как и всегда в своих суждениях и чувствах не зная середины, по слухам о буйстве и своевольстве этого помещика, всей душой ненавидел его и считал своим злейшим врагом. Он озлобленно взволнованный ехал теперь к нему, крепко сжимая арапник в руке, в полной готовности на самые решительные и опасные действия против своего врага.
Едва он выехал за уступ леса, как он увидал подвигающегося ему навстречу толстого барина в бобровом картузе на прекрасной вороной лошади, сопутствуемого двумя стремянными.
Вместо врага Николай нашел в Илагине представительного, учтивого барина, особенно желавшего познакомиться с молодым графом. Подъехав к Ростову, Илагин приподнял бобровый картуз и сказал, что очень жалеет о том, что случилось; что велит наказать охотника, позволившего себе травить из под чужих собак, просит графа быть знакомым и предлагает ему свои места для охоты.
Наташа, боявшаяся, что брат ее наделает что нибудь ужасное, в волнении ехала недалеко за ним. Увидав, что враги дружелюбно раскланиваются, она подъехала к ним. Илагин еще выше приподнял свой бобровый картуз перед Наташей и приятно улыбнувшись, сказал, что графиня представляет Диану и по страсти к охоте и по красоте своей, про которую он много слышал.
Илагин, чтобы загладить вину своего охотника, настоятельно просил Ростова пройти в его угорь, который был в версте, который он берег для себя и в котором было, по его словам, насыпано зайцев. Николай согласился, и охота, еще вдвое увеличившаяся, тронулась дальше.
Итти до Илагинского угоря надо было полями. Охотники разровнялись. Господа ехали вместе. Дядюшка, Ростов, Илагин поглядывали тайком на чужих собак, стараясь, чтобы другие этого не замечали, и с беспокойством отыскивали между этими собаками соперниц своим собакам.
Ростова особенно поразила своей красотой небольшая чистопсовая, узенькая, но с стальными мышцами, тоненьким щипцом (мордой) и на выкате черными глазами, краснопегая сучка в своре Илагина. Он слыхал про резвость Илагинских собак, и в этой красавице сучке видел соперницу своей Милке.
В середине степенного разговора об урожае нынешнего года, который завел Илагин, Николай указал ему на его краснопегую суку.
– Хороша у вас эта сучка! – сказал он небрежным тоном. – Резва?
– Эта? Да, эта – добрая собака, ловит, – равнодушным голосом сказал Илагин про свою краснопегую Ерзу, за которую он год тому назад отдал соседу три семьи дворовых. – Так и у вас, граф, умолотом не хвалятся? – продолжал он начатый разговор. И считая учтивым отплатить молодому графу тем же, Илагин осмотрел его собак и выбрал Милку, бросившуюся ему в глаза своей шириной.
– Хороша у вас эта чернопегая – ладна! – сказал он.
– Да, ничего, скачет, – отвечал Николай. «Вот только бы побежал в поле матёрый русак, я бы тебе показал, какая эта собака!» подумал он, и обернувшись к стремянному сказал, что он дает рубль тому, кто подозрит, т. е. найдет лежачего зайца.
– Я не понимаю, – продолжал Илагин, – как другие охотники завистливы на зверя и на собак. Я вам скажу про себя, граф. Меня веселит, знаете, проехаться; вот съедешься с такой компанией… уже чего же лучше (он снял опять свой бобровый картуз перед Наташей); а это, чтобы шкуры считать, сколько привез – мне всё равно!
– Ну да.
– Или чтоб мне обидно было, что чужая собака поймает, а не моя – мне только бы полюбоваться на травлю, не так ли, граф? Потом я сужу…
– Ату – его, – послышался в это время протяжный крик одного из остановившихся борзятников. Он стоял на полубугре жнивья, подняв арапник, и еще раз повторил протяжно: – А – ту – его! (Звук этот и поднятый арапник означали то, что он видит перед собой лежащего зайца.)
– А, подозрил, кажется, – сказал небрежно Илагин. – Что же, потравим, граф!
– Да, подъехать надо… да – что ж, вместе? – отвечал Николай, вглядываясь в Ерзу и в красного Ругая дядюшки, в двух своих соперников, с которыми еще ни разу ему не удалось поровнять своих собак. «Ну что как с ушей оборвут мою Милку!» думал он, рядом с дядюшкой и Илагиным подвигаясь к зайцу.
– Матёрый? – спрашивал Илагин, подвигаясь к подозрившему охотнику, и не без волнения оглядываясь и подсвистывая Ерзу…
– А вы, Михаил Никанорыч? – обратился он к дядюшке.
Дядюшка ехал насупившись.
– Что мне соваться, ведь ваши – чистое дело марш! – по деревне за собаку плачены, ваши тысячные. Вы померяйте своих, а я посмотрю!
– Ругай! На, на, – крикнул он. – Ругаюшка! – прибавил он, невольно этим уменьшительным выражая свою нежность и надежду, возлагаемую на этого красного кобеля. Наташа видела и чувствовала скрываемое этими двумя стариками и ее братом волнение и сама волновалась.
Охотник на полугорке стоял с поднятым арапником, господа шагом подъезжали к нему; гончие, шедшие на самом горизонте, заворачивали прочь от зайца; охотники, не господа, тоже отъезжали. Всё двигалось медленно и степенно.
– Куда головой лежит? – спросил Николай, подъезжая шагов на сто к подозрившему охотнику. Но не успел еще охотник отвечать, как русак, чуя мороз к завтрашнему утру, не вылежал и вскочил. Стая гончих на смычках, с ревом, понеслась под гору за зайцем; со всех сторон борзые, не бывшие на сворах, бросились на гончих и к зайцу. Все эти медленно двигавшиеся охотники выжлятники с криком: стой! сбивая собак, борзятники с криком: ату! направляя собак – поскакали по полю. Спокойный Илагин, Николай, Наташа и дядюшка летели, сами не зная как и куда, видя только собак и зайца, и боясь только потерять хоть на мгновение из вида ход травли. Заяц попался матёрый и резвый. Вскочив, он не тотчас же поскакал, а повел ушами, прислушиваясь к крику и топоту, раздавшемуся вдруг со всех сторон. Он прыгнул раз десять не быстро, подпуская к себе собак, и наконец, выбрав направление и поняв опасность, приложил уши и понесся во все ноги. Он лежал на жнивьях, но впереди были зеленя, по которым было топко. Две собаки подозрившего охотника, бывшие ближе всех, первые воззрились и заложились за зайцем; но еще далеко не подвинулись к нему, как из за них вылетела Илагинская краснопегая Ерза, приблизилась на собаку расстояния, с страшной быстротой наддала, нацелившись на хвост зайца и думая, что она схватила его, покатилась кубарем. Заяц выгнул спину и наддал еще шибче. Из за Ерзы вынеслась широкозадая, чернопегая Милка и быстро стала спеть к зайцу.
– Милушка! матушка! – послышался торжествующий крик Николая. Казалось, сейчас ударит Милка и подхватит зайца, но она догнала и пронеслась. Русак отсел. Опять насела красавица Ерза и над самым хвостом русака повисла, как будто примеряясь как бы не ошибиться теперь, схватить за заднюю ляжку.
– Ерзанька! сестрица! – послышался плачущий, не свой голос Илагина. Ерза не вняла его мольбам. В тот самый момент, как надо было ждать, что она схватит русака, он вихнул и выкатил на рубеж между зеленями и жнивьем. Опять Ерза и Милка, как дышловая пара, выровнялись и стали спеть к зайцу; на рубеже русаку было легче, собаки не так быстро приближались к нему.
– Ругай! Ругаюшка! Чистое дело марш! – закричал в это время еще новый голос, и Ругай, красный, горбатый кобель дядюшки, вытягиваясь и выгибая спину, сравнялся с первыми двумя собаками, выдвинулся из за них, наддал с страшным самоотвержением уже над самым зайцем, сбил его с рубежа на зеленя, еще злей наддал другой раз по грязным зеленям, утопая по колена, и только видно было, как он кубарем, пачкая спину в грязь, покатился с зайцем. Звезда собак окружила его. Через минуту все стояли около столпившихся собак. Один счастливый дядюшка слез и отпазанчил. Потряхивая зайца, чтобы стекала кровь, он тревожно оглядывался, бегая глазами, не находя положения рукам и ногам, и говорил, сам не зная с кем и что.
«Вот это дело марш… вот собака… вот вытянул всех, и тысячных и рублевых – чистое дело марш!» говорил он, задыхаясь и злобно оглядываясь, как будто ругая кого то, как будто все были его враги, все его обижали, и только теперь наконец ему удалось оправдаться. «Вот вам и тысячные – чистое дело марш!»
– Ругай, на пазанку! – говорил он, кидая отрезанную лапку с налипшей землей; – заслужил – чистое дело марш!
– Она вымахалась, три угонки дала одна, – говорил Николай, тоже не слушая никого, и не заботясь о том, слушают ли его, или нет.
– Да это что же в поперечь! – говорил Илагинский стремянный.
– Да, как осеклась, так с угонки всякая дворняшка поймает, – говорил в то же время Илагин, красный, насилу переводивший дух от скачки и волнения. В то же время Наташа, не переводя духа, радостно и восторженно визжала так пронзительно, что в ушах звенело. Она этим визгом выражала всё то, что выражали и другие охотники своим единовременным разговором. И визг этот был так странен, что она сама должна бы была стыдиться этого дикого визга и все бы должны были удивиться ему, ежели бы это было в другое время.
Дядюшка сам второчил русака, ловко и бойко перекинул его через зад лошади, как бы упрекая всех этим перекидыванием, и с таким видом, что он и говорить ни с кем не хочет, сел на своего каураго и поехал прочь. Все, кроме его, грустные и оскорбленные, разъехались и только долго после могли притти в прежнее притворство равнодушия. Долго еще они поглядывали на красного Ругая, который с испачканной грязью, горбатой спиной, побрякивая железкой, с спокойным видом победителя шел за ногами лошади дядюшки.
«Что ж я такой же, как и все, когда дело не коснется до травли. Ну, а уж тут держись!» казалось Николаю, что говорил вид этой собаки.
Когда, долго после, дядюшка подъехал к Николаю и заговорил с ним, Николай был польщен тем, что дядюшка после всего, что было, еще удостоивает говорить с ним.
Когда ввечеру Илагин распростился с Николаем, Николай оказался на таком далеком расстоянии от дома, что он принял предложение дядюшки оставить охоту ночевать у него (у дядюшки), в его деревеньке Михайловке.
– И если бы заехали ко мне – чистое дело марш! – сказал дядюшка, еще бы того лучше; видите, погода мокрая, говорил дядюшка, отдохнули бы, графинечку бы отвезли в дрожках. – Предложение дядюшки было принято, за дрожками послали охотника в Отрадное; а Николай с Наташей и Петей поехали к дядюшке.