Длинная арифметика

Длинная арифметика — выполняемые с помощью вычислительной машины арифметические операции (сложение, вычитание, умножение, деление, возведение в степень, элементарные функции) над числами, разрядность которых превышает длину машинного слова данной вычислительной машины. Эти операции реализуются не аппаратно, а программно, с использованием базовых аппаратных средств работы с числами меньших порядков. Частный случай — арифметика произвольной точности — относится к арифметике, в которой длина чисел ограничена только объёмом доступной памяти.

Применение

Длинная арифметика применяется в следующих областях:

• составление кода для процессоров (микроконтроллеров) низкой разрядности. Например, микроконтроллеры серии AVR имеют АЦП с разрядностью 10 бит и регистры с разрядностью 8 бит. Этого недостаточно для обработки информации с АЦП; без длинной арифметики не обойтись;
• криптография. Большинство систем подписывания и шифрования данных используют целочисленную арифметику по модулю m, где m — очень большое натуральное число, не обязательно простое. Например, при реализации метода шифрования RSA, криптосистемы Рабина или схемы Эль-Гамаля требуется обеспечить точность результатов умножения и возведения в степень порядка 10³⁰⁹;
• математическое (см. список ПО) и финансовое ПО. Результат вычисления на бумаге должен совпадать с результатом работы компьютера с точностью до последнего разряда. В частности, калькулятор Windows (начиная с Windows 95) проводит четыре арифметических действия с намного большей точностью, чем позволяет процессор x86. Для научных и инженерных расчётов длинная арифметика применяется редко, так как ошибки во входных данных обычно намного больше, чем ошибки округления;
• стандартная тема в спортивном программировании. В настоящее время (2010-е) выходит из моды из-за «заезженности» и дискриминации по языку (в некоторых языках есть встроенные библиотеки). Если задача оперирует большими числами, но не хочется подключать длинную арифметику, автор может сказать: «вывести последние 32 бита ответа».

Необходимые аппаратные средства для работы с длинной арифметикой

Строго говоря, для реализации арифметики произвольной точности от процессора требуется лишь косвенная адресация; в арифметике фиксированной точности можно обойтись даже без неё. Тем не менее, определённые функции процессора ускоряют длинную арифметику, одновременно упрощая её программирование.

• Флаг переноса. Операции «сложить/вычесть с переносом», «циклический сдвиг через бит переноса».
• Автоинкрементные и автодекрементные операции доступа к памяти.
• Умножение w · w = (w²), деление (w²) / w = w.

Реализация в языках программирования

Языки программирования имеют встроенные типы данных, размер которых, в основном, не превышает 64 бита (около 10¹⁹). Десятичная длинная арифметика была реализована в советских языках программирования АЛМИР-65 на ЭВМ МИР-1 и АНАЛИТИК на ЭВМ МИР-2.
Для работы с большими числами, в современных языках программирования существует довольно много готовых оптимизированных библиотек для длинной арифметики.

• GNU Multi-Precision Library
• LibTomMath

Большинство функциональных языков позволяют переключаться с обычной арифметики на длинную без необходимости изменения кода арифметических расчётов. Например, Erlang и Scheme всегда представляют точные числа длинными. В Standard ML реализации всех разновидностей целых чисел определяются на основании сигнатуры INTEGER, позволяя выбирать необходимую размерность,— в том числе присутствует модуль IntInf, реализующий целые числа произвольной точности; в реализации PolyML этот модуль используется по умолчанию.

Встроенные библиотеки работы с большими числами есть в Ruby, Python и Java.

Алгоритмы

Алгоритмы умножения

Для описания алгоритмов обычно используется следующее представление целых чисел. Выбирается основание <math>\beta > 1 </math>. Тогда целое число длины <math>n</math> можно представить в виде:

<math>A=a_{n-1} \cdot \beta^{n-1} + ... + a_1 \cdot \beta + a_0,</math>

где <math> 0 \le a_i \le \beta - 1.</math>

Базовый

Представляет собой алгоритм по школьному методу «в столбик». Занимает время <math>O(n \cdot m),</math> где <math>n, m</math> — размеры перемножаемых чисел.

Алгоритм может быть представлен в виде:

Algorithm 1 BasecaseMultiply
Input: <math>A=\sum\nolimits_{i=0}^{m-1} a_i \beta^i, B=\sum\nolimits_{j=0}^{n-1} b_j \beta^j </math>
Output: <math>C=AB:=\sum\nolimits_{k=0}^{m+n-1} c_k \beta^k </math>
<math>1: C \gets A\cdot b_0</math>
<math>2:</math> for <math>j</math> from <math>1</math> to <math>n-1</math> do
<math>3: ~~~~C \gets C + \beta^j(A \cdot b_j)</math>
<math>4: return~~C.</math>

Умножение Карацубы

Метод умножения Карацубы относится к парадигме «разделяй и властвуй». Сложность вычисления алгоритма:

<math>M(n)=O(n^{\log_23}),\quad\log_23=1{,}5849\ldots</math>.

Данный алгоритм представляет собой простую реализацию идеи разделения входных данных, которая стала базисной для нижеперечисленных алгоритмов. Идея заключается в разделении одной операции умножения над <math>n</math>-значными числами на три операции умножения над числами длины <math>n/2</math> плюс <math>O(n)</math>.

Для перемножения двух чисел, превышающих длину машинного слова, алгоритм Карацубы вызывается рекурсивно до тех пор, пока эти числа не станут достаточно маленькими, чтобы их можно было перемножить непосредственно. Пример такого алгоритма:

Algorithm 2 KaratsubaMultiply
Input: <math>A=\sum\nolimits_{i=0}^{n-1} a_i \beta^i, B=\sum\nolimits_{j=0}^{n-1} b_j \beta^j </math>
Output: <math>C=AB:=\sum\nolimits_{k=0}^{2n-1} c_k \beta^k </math>
<math>k \gets [n/2]</math>
<math>(A_0, B_0):=(A, B)mod \beta^k, (A_1, B_1):=(A, B)div \beta^k</math>
<math>s_A \gets sign(A_0-A_1), s_B \gets sign(B_0-B_1)</math>
<math>C_0 \gets</math> KaratsubaMultiply<math>(A_0,B_0)</math>
<math>C_1 \gets</math> KaratsubaMultiply<math>(A_1,B_1)</math>
<math>C_2 \gets</math> KaratsubaMultiply<math>(|A_0-A_1|,|B_0-B_1|)</math>
<math>return~C:=C_0+(C_0+C_1-s_As_BC_2) \beta^k + C_1 \beta^{2k}</math>

Посчитаем <math>x = 12345 \cdot 6789</math>:

<math>12345 = 12 \cdot 1000 + 345</math>

<math>6789 = 6 \cdot 1000 + 789</math>

Нужно вычислить три промежуточных коэффициента:

<math>C_0 = 345 \cdot 789 = 272205</math>

<math>C_1 = 12 \cdot 6 = 72</math>

<math>C_2 = C_1 + C_0 - (345 - 12) \cdot (789 - 6) = 72 + 272205 -333 \cdot 783 = 11538</math>

Результат:

<math>x = C_1 \cdot 1000^2 + C_2 \cdot 1000 + C_0 </math>

<math>x = 72 \cdot 1000^2 + 11538 \cdot 1000 + 272205 = 83810205</math>

Алгоритм Тоома

Этот алгоритм является обобщением алгоритма Карацубы и работает быстрее. Для двух данных целых чисел <math>A</math> и <math>B</math> алгоритм Toom-a делит их на <math>k</math> меньших частей, длина каждой из которых равна длине машинного слова, и производит операции над этими частями. Сложность вычисления алгоритма: <math>O(n^{\ln(2k-1)/\ln(k)}).</math>

Алгоритм Тоома-3

Идея впервые была предложена А. Л. Тоомом в 1963 году, и заключается в разделении входных данных (множителей) на 3 равные части (для простоты все части считаем равными). Toom-3 сокращает число элементарных операций умножения с 9 до 5. Сложность алгоритма <math>O(n^{1.465}).</math>

Рассмотрим данный алгоритм на следующем примере. Пусть дано два числа <math>Y</math> и <math>X</math>. Пусть определены операции над числами, размер которых равен 1/3 от размеров исходных чисел (см. рисунок). Предположим также, что числа занимают равную память и делятся ровно на 3 части, в противном случае дополним оба числа нулями до необходимых размеров.

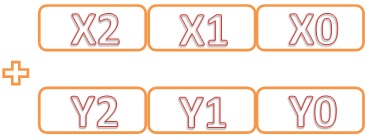
Затем происходит отображение (параметризация) этих частей на полиномы 2 степени.

<math>X(t) = x_2 \cdot t^2 + x_1 \cdot t + x_0,</math>

<math>Y(t) = y_2 \cdot t^2 + y_1 \cdot t + y_0,</math>

Введем <math>b</math>, по определению такую, что значения многочленов <math>X(b),~Y(b)</math> соответственно равны входным числам <math>x</math> и <math>y</math>. Для битового представления чисел это число равно двойке в степени, равной длине каждой из частей в битах.

Также введем полином:

<math>W(t)=X(t) \cdot Y(t),</math> (1)

<math>W(t) = w_4 \cdot t^4 + w_3 \cdot t^3 + w_2 \cdot t^2 + w_1 \cdot t + w_0,</math>

После того как будут определены элементы <math>w_i</math> — коэффициенты многочлена<math>W(t)</math>, они будут использованы в целях получения <math>w=W(b)</math>, так как <math>x \cdot y=X(b) \cdot Y(b)=W(b)</math>. Размер коэффициентов <math>w_i</math> в 2 раза больше (по памяти), чем разбиение <math>x_i</math> или <math>y_i</math>. Конечное число, равное произведению <math>x \cdot y</math> можно найти, складывая <math>w_i</math> со сдвигом, как показано на рисунке ниже. Коэффициенты <math>w_i</math> могут быть вычислены следующим образом: <math>w_4=x_2 \cdot y_2, w_3=x_2 \cdot y_1+x_1 \cdot y_2,~~ w_2=x_2 \cdot y_0+x_1 \cdot y_1+x_0 \cdot y_2 </math> и так далее, но это потребует все 9 перемножений: <math>x_i \cdot y_j</math> для i, j=0,1,2, и будет эквивалентно простому перемножению.

Вместо этого был использован иной подход. <math>X(t),Y(t)</math> вычисляются в (1) в 5 точках при разных <math>t</math>.

В таблице, представленной ниже, приведены значения полиномов в равенстве (1)

<math>t=0</math>	<math>x_0 \cdot y_0</math>	<math>W(0)~~~=~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~w_0</math>
<math>t=1</math>	<math>(x_2+x_1+x_0) \cdot (y_2+y_1+y_0)</math>	<math>W(1)~~~=~~~~w_4 + ~w_3 + ~~w_2 + ~w_1 + w_0</math>
<math>t=-1</math>	<math>(x_2-x_1+x_0) \cdot (y_2-y_1+y_0)</math>	<math>W(-1)~=~~~~w_4 - ~w_3 + ~~w_2 - ~w_1 + w_0</math>
<math>t=2</math>	<math>(4x_2+2x_1+x_0) \cdot (4y_2+2y_1+y_0)</math>	<math>W(2)~~~=~16w_4 + 8w_3 + 4w_2 + 2w_1 + w_0</math>
<math>t= \infty </math>	<math>x_2 \cdot y_2</math>	<math>W(\infty)~~=~~~~w_4</math>

Параметр <math>t=\infty</math> условный. Он означает банальное равенство коэффициентов при <math>t^4</math>, тем самым мы получим значение <math>w_4</math> сразу. Данная система линейна относительно 5 неизвестных. При её разрешении мы получаем неизвестные <math>w_i</math>. Далее получаем значение многочлена, как было описано выше.

Алгоритм Тоома-4

Сложность алгоритма <math>O(n^{1.404}).</math> Представляет собой 7 элементарных операций умножения. Toom-4 разделяет входные данные на 4 части.

По такому же принципу как и в Toom-3 строим два полинома:

<math>X(t) = x3 \cdot t^3 + x2 \cdot t^2 + x1 \cdot t + x0,</math>

<math>Y(t) = y3 \cdot t^3 + y2 \cdot t^2 + y1 \cdot t + y0.</math>

<math>X(t)</math> и <math>Y(t)</math> вычисляются в 7 разных точках, также вычисляется значение <math>W(t)</math> в этих точках.

<math>t=0</math>	<math>x_0 \cdot y_0,</math> откуда сразу получаем <math>w_0</math>
<math>t=1/2</math>	<math>(x_3+2x_2+4x_1+8x_0) \cdot (y_3+2y_2+4y_1+8y_0)</math>
<math>t=-1/2</math>	<math>(-x_3+2x_2-4x_1+8x_0) \cdot (-y_3+2y_2-4y_1+8y_0)</math>
<math>t=1</math>	<math>(x_3+x_2+x_1+x_0) \cdot (y_3+y_2+y_1+y_0)</math>
<math>t=-1</math>	<math>(-x_3+x_2-x_1+x_0) \cdot (-y_3+y_2-y_1+y_0)</math>
<math>t=2</math>	<math>(8x_3+4x_2+2x_1+x_0) \cdot (8y_3+4y_2+2y_1+y_0)</math>
<math>t=\infty</math>	<math>x_3 \cdot y_3,</math> откуда сразу получаем <math>w_6</math>

Количество операций сложения и умножения для Toom-4 намного больше, чем для Toom-3. Но некоторые выражения встречаются по нескольку раз. Например, <math>x_2+x_0</math> вычисляется для <math>t=1</math> и для <math>t=-1</math>.

Алгоритм Тоома для произвольного разбиения

Алгоритм Тоома для разделения входных чисел на n операндов эквивалентен описанному выше. В общем случае разделение двух одинаково длинных операндов на <math>r</math> частей приводит к вычислению значений в <math>2r-1</math> точках. В качестве точек для решения системы, обычно берут <math>0, \infty, +1, -1 , \pm 2^i, \pm 2^{-i}</math>.

Перемножение методом Фурье

Данный алгоритм перемножения используется для больших и очень больших чисел.

Этот алгоритм перемножает два числа за время <math> O(n \cdot \log n),</math> где <math>n</math> — количество значащих цифр в перемножаемых числах (предполагая их равными). Создание приписывается Кули (Coolet) и Таки (Tukey) — 1965 г. Также есть предположения, что данный алгоритм был известен и раньше, но не имел большой важности до того как изобрели первые компьютеры. Вероятными кандидатами на авторство изобретения данного алгоритма также называют Рунг (Runge) и Кёниг (Konig) — 1924 г., а также Гаусса — 1805 г.

Пусть имеется число, представим его в виде многочлена, как мы делали ранее. Назовем этот многочлен <math>A(x).</math> Также введем дискретное преобразование Фурье многочлена как вектор, с координатами <math>\left (b_1, b_2, b_3, b_4, \dots b_{n-1}\right )</math>. Где <math>b[i]</math> определены как <math>w^n[i]</math> — комплексный корень <math>n</math>-ой степени из 1, не равный 1. Дело в том, что комплексный корень из 1 определен с точностью до фазового множителя, количество этих корней — <math>n</math>. Преобразование Фурье применено для того, чтобы свертку коэффициентов многочленов <math>A</math> и <math>B</math>: <math>(A(x) \cdot B(x))</math> — заменить на произведение их Фурье образов.

<math>F(A(x) \cdot B(x)) = F (A) \cdot F (B)</math>

<math> A(x) \cdot B(x) = F^{-1} (F (A) \cdot F (B)),</math>

где под умножением <math>F(A)\cdot F(B)</math> подразумевается скалярное произведение векторов.

Предположим, что <math>n</math> есть степень двойки.

Нахождение <math>F(A)</math> производится рекурсивным методом (разделяй и властвуй). Идея заключается в разбиении исходного многочлена <math>A (x) = a_0 x_0 + a_1 x_1 + ... + a_{n-1}x_{n-1}</math> на два многочлена,

<math>A0 (x) = a_0x_0 + a_2x_1 + a_4x_2 + \dots + a_{n-2}x_{\frac{n-2}{2}}</math>

<math>A1 (x) = a_1x_0 + a_3x_1 + a_5x_2 + \dots + a_{n-1}x_{\frac{n-2}{2}}</math>

Тогда <math>A(x) = A0 (x^2) + x \cdot A1 (x^2)</math>.

Заметим, что среди всех чисел <math>\left (w^n_i\right )^2 (0 \leq i < n)</math>, только <math>\frac{n}{2}</math> различных. Поэтому, ДПФ <math>A0</math> и <math>A1</math> будут <math>\frac{n}{2}</math>-элементными. А так как ДПФ <math>A0</math> и <math>A1</math> состоит из <math>\frac{n}{2}</math> элементов, то комплексным корнем из 1 там будет корень степени <math>\frac{n}{2}</math>.

Значит,

<math>A(w^n_k) = A0(w^n_{2k}) + w^n_k \cdot A1(w^n_{2k}) = A0(w^\frac{n}{2}_k) + w^n_k \cdot A1(w^\frac{n}{2}_k),</math>

где <math>0 \leq k < n / 2</math> и

<math>A(w^n_{k+\frac{n}{2}}) = A0(w^n_{2 \cdot {k+\frac{n}{2}}}) + w^n_{k+\frac{n}{2}} \cdot A1(w^n_{2 \cdot {k+\frac{n}{2}}}) = A0(w^{n/2}_{k+\frac{n}{2}}) + w^n_{k+\frac{n}{2}} \cdot A1(w^\frac{n}{2}_{k+\frac{n}{2}}) = A0(w^\frac{n}{2}_k) - w^n_k \cdot A1(w^\frac{n}{2}_k).</math>

Мы использовали свойства комплексных чисел: различных корней степени <math>n</math> всего <math>n</math>. <math>w^n_{k+\frac{n}{2}} = w^n_k \cdot e^{i \cdot \frac{2\pi}{n} \cdot \frac{n}{2}} = w^n_k \cdot e^{i \cdot \pi} = - w^n_k</math>.

Получаем рекурсивный алгоритм:
ДПФ одного элемента равно этому элементу
для нахождения ДПФ A разбиваем коэффициенты A на чётные и нечётные, получаем два многочлена <math>A0</math> и <math>A1</math>, находим ДПФ для них, находим ДПФ <math>A</math>:
<math>b_k = b^0_k + w^n_k \cdot b^1_k</math>
<math>b_{k + \frac{n}{2}} = b^0_k - w^n_k \cdot b^1_k</math>
для <math>0 \leq k < n / 2</math>.
Существует доказательство следующего утверждения: Обратное ДПФ находится аналогично прямому ДПФ, за исключением того, что в качестве точек берутся точки, симметричные относительно вещественной оси, вместо тех, что использовались в прямом ДПФ преобразовании. Также необходимо все коэффициенты многочлена поделить на n

Алгоритмы извлечения корня

Квадратный корень

Одним из алгоритмов вычисления квадратного корня является алгоритм «Karatsuba Square Root». На данный момент это самый известный метод вычисления квадратного корня n-значного числа. Этот алгоритм использует быстрое преобразование Фурье и метод Ньютона со сложностью 5M(n).

Представленный алгоритм основан на делении Бурникеля — Циглера (Burnikel-Ziegler) Карацубы. Имея целое число n, алгоритм подсчитывает одновременно его целый квадратный корень <math>s = \lfloor \sqrt{n} \rfloor</math> и соответствующий остаток, который равен <math>r = n-s^2.</math> Это не является асимптотически оптимальным, но очень эффективно на практике со сложностью порядка <math>\frac{3}{2}K(n)</math> операций, где K(n) — это количество операций, необходимых чтобы умножить два n-разрядных числа, используя алгоритм Карацубы (Karatsuba). Причина этой низкой сложности в красивом делении Карацубы (Karatsuba), недавно открытом Бурникелем и Циглером (Burnikel and Ziegler), а также в осторожном обращении с остатками, которое избегает ненужных вычислений.

Теорема. Число операций, которые алгоритм SqrtRem использует со 2n-разрядным входом, ограничено

<math>\frac{3}{2}K(n)+O(n \log n),</math>

где K(n) — число операций, необходимых для умножения 2n-разрядных чисел, используя алгоритм Карацубы.

Algorithm SqrtRem <math> (n = a_{3}b_{3}+a_{2}b_{2}+a_{1}b+a_{0}) </math>
~<math> Input: 0 \le a_{i} \le b ~ with~ a_{3} \ge b/4 </math>
<math> Output: (s,r)~ such~ that~ s^2 \le n = s^2 + r < (s+1)^2 </math>
<math> (s', r') \leftarrow SqrtRem(a_{3}b+a_{2}) </math>
<math> (q,u) \leftarrow DivRem(r'b+a_{1},2s') </math>
<math> s \leftarrow ub+a_{0}-q^2 </math>
<math> if ~r < 0 ~then</math>
<math> r \leftarrow r+2s-1 </math>
<math> s \leftarrow s-1 </math>
<math> return (s,r) </math>

Алгоритмы преобразования системы счисления

Предположим, что выполняется преобразование из системы счисления по осно­ванию b в систему счисления по основанию В.

Способы преобразования целых чисел

Метод 1 (Деление на В с использованием представления чисел в формате по основанию b). Для заданного целого числа и можно
получить представление в формате по основанию В вида <math> ( \dots U_{2}U_{1}U_{0})_{B} </math>, выполняя

<math> U_{0} = u\!\!\!\! \mod B </math>, <math> U_{1}= \left \lfloor \frac{u}{B} \right \rfloor\!\!\!\! \mod B </math>, <math> U_{2} = \left \lfloor \left \lfloor \frac{u}{B} \right \rfloor \right \rfloor\!\!\!\!\mod B </math>, до тех пор, пока не окажется <math> \left \lfloor \dots { \left \lfloor { \left \lfloor \frac{u}{B} \right \rfloor }  \right \rfloor }  {\dots/B}  \right \rfloor =0  </math>.

Метод 2 (Умножение на В с использованием представления чисел в формате по основанию b). Если представление числа и по основанию b имеет вид <math> (u_{m}\dots u_{1}u_{0})_{b} </math>, то можно, воспользовавшись арифметическими операциями с числами, которые представлены в формате по основанию В, получить полином <math> u_{m}b^{m}+\dots+u_{1}b+u_{m}u_{0}=u </math> в виде
((<math>\dots ( u_{m}b + u_{m-1}){b} + \dots) b + u_{1}b + u_{0} </math> .

Способы преобразования целых чисел

Метод 1 (a) (Умножение на b с использованием представления чисел в формате по основанию В). Для данного дробного числа и можно вычислить значения разрядов <math> (.U_{-1}U_{-2} ... )_{B} </math> его представления по основанию В следующим образом:
<math> U_{-1}= \left \lfloor \ {uB} \right \rfloor </math>, <math> U_{-2} {=} \left \lfloor \ {{uB}B}\right \rfloor </math>, <math> U_{-3}= \left \lfloor \ {((uB)B)B} \right \rfloor </math> ,… где {х} означает xmod1 = х- <math> \left \lfloor \ {x} \right \rfloor </math>. Чтобы округлить результат до М разрядов, вычисления можно прервать после получения <math> U_{M} </math>, причем если {…{{uВ}В}...В} больше 1/2, то значение <math> U_{M} </math> следует увеличить на единицу. (Заметим, однако, что эта операция может привести к необходимости выполнения переносов, которые должны быть при помощи арифметических операций по основанию В включены в результат. Было бы проще перед началом вычислений прибавить к исходному числу u константу <math> 1/2 B^{-M} </math>, но это может привести к неправильному результату, если в компьютере число <math> 1/2 B^{-M} </math> не может быть точно представлено в формате по основанию b. Заметим также, что возможно округление результата до <math> (1.00...0)^B </math>, если <math> b^{m} </math> <math> \geq </math> <math> 2B^{M} </math> ).
Метод 2 (a) (Умножение на В с использованием представления чисел в формате по основанию b). Если представление числа и по основанию b имеет вид <math> (u_{m}{...}u_{1}u_{0})_{b} </math>, то можно, воспользовавшись арифметическими операциями с числами, которые представлены в формате по основанию В, получить полином <math> u_{m}b^{m}+{...}+u_{1}b+u_{m}u_{0}=u </math> в виде
(( … <math> ( u_{m}b + u_{m-1}){b} </math> + …) <math> b </math> + <math> u_{1}b + u_{0} </math> .

Способы преобразования дробных чисел

Метод 1 (b) (Умножение на b с использованием представления чисел в формате по основанию В). Для данного дробного числа u можно вычислить значения разрядов <math> (0.U_{-1}U_{-2} ... )_{B} </math> его представления по основанию В следующим образом:
<math> U_{-1}= \left \lfloor \ {uB} \right \rfloor </math>, <math> U_{-2} {=} \left \lfloor \ {{uB}B}\right \rfloor </math>, <math> U_{-3}= \left \lfloor \ {((uB)B)B} \right \rfloor </math> ,... где {х} означает xmod1 = х- <math> \left \lfloor \ {x} \right \rfloor </math>. Чтобы округлить результат до М разрядов, вычисления можно прервать после получения <math> U_{M} </math>, причем если {...{{uВ}В}...В} больше 1/2, то значение <math> U_{M} </math> следует увеличить на единицу. (Заметим, однако, что эта операция может привести к необходимости выполнения переносов, которые должны быть при помощи арифметических операций по основанию В включены в результат. Было бы проще перед началом вычислений прибавить к исходному числу u константу <math> 1/2 B^{-M} </math>, но это может привести к неправильному результату, если в компьютере число <math> 1/2 B^{-M} </math> не может быть точно представлено в формате по основанию b. Заметим также, что возможно округление результата до <math> (1.00...0)^B </math>, если <math> b^{m} </math> <math> \geq </math> <math> 2B^{M} </math> ).

Метод 2 (b)(Деление на b с использованием представления чисел в формате по основанию В). Если число u представлено по основанию b в виде <math> (0.u_{-1}u_{-2} ... u_{-m})_{b} </math>, то можно, используя арифметические операции по основанию В, вычислить <math> u_{-1}b^{-1}+u_{-2}b^{-2}+{...}+u_{-m}b{-m} </math> в виде
<math> ((... (u_{-m}/b + u_{1-m})/b + ... + u_{-2})/b + u_{-1})/b </math>. Необходимо внимательно следить за погрешностями, возникающими при усечениях или округлениях во время выполнения операции деления на b; они, как правило, незначительны, но это бывает не всегда.

Преобразование с многократной точностью

Начинать преобразование очень длинных чисел удобнее всего с преобразования блоков разрядов, операции с которыми можно выполнять с однократной точностью. Затем следует объединить эти блоки, пользуясь простыми способами, которые специфичны для многократной точности. Например, пусть 10n-наивысшая степень 10, меньшая, чем размер машинного слова. Тогда:
а) чтобы преобразовать целое "Число с многократной точностью из двоичного формата в десятичный, необходимо многократно разделить его на 10n (выполняя таким образом преобразование из двоичной системы счисления в десятичную с основанием 10n по методу 1, а); при помощи операций с однократной точностью получим n десятичных разрядов для каждой единицы представления в системе счисления с основанием 10n;
b) чтобы преобразовать дробную "Часть числа с многократной точностью из двоичного формата в десятичный, поступим подобным образом, умножив его на <math> 10^n </math>: (т.е. использовав метод 2, а, где В= 10n);
с) чтобы преобразовать целое число с многократной точностью из десятичной системы счисления в двоичную, преобразуем сначала блоки по n разрядов; затем для перехода из системы счисления с основанием 10n в двоичный формат используем метод 1, b;
d) для преобразования дробной части с многократной точностью из представления в десятичном формате в двоичный сначала выполним преобразование в систему с основанием 10n, как и в процедуре (с), а затем используем метод 2, b.

Алгоритмы деления

Алгоритм деления n-битового числа u на n-битовое число v должен выдавать результатом два n-битовых числа - u mod v и u div v. Описанные ниже алгоритмы не применимы на практике, так как находят вещественное число, а не два n-битовых числа, результата деления.

В теории чтобы разделить n-битовое число u на n - битовое число v, можно сначала найти n-битовое приближение к числу 1/v, затем умножить его на u, что даст приближение <math> \hat{q} </math> к <math> u/v </math> , И наконец выполнить еще одно умножение для внесения небольшой коррекции в <math> \hat{q} </math> , чтобы убедиться, что выполняется неравенство <math> 0 \le u-qv < v </math> . Исходя из сказанного, достаточно иметь эффективный алгоритм, который формировал бы по заданному n-битовому числу приближенное значение числа, обратного n-битовому числу. Далее применить алгоритм умножения n-битовых чисел.

Алгоритм R (Получение обратной величины с высокой точностью) Пусть число v имеет двоичное представление <math> v=(0.v_{1}v_{2}v_{3})_{2} </math>, где <math> v_{1}=1 </math>. Этот алгоритм вычисляет приближение z числа <math> 1/v </math>, такое, что
<math> |z-1/v| \le 2^{-n} </math>.
R1(Начальное приближение) Присвоить <math> z \leftarrow \frac{1}{4} \left \lfloor \frac{32}{(4v_{1}+2v_{2}+v_{3})} \right \rfloor </math> и <math> k \leftarrow 0 </math>.
R2 (Итерация по Ньютону) Здесь имеем число z в двоичном виде <math> (xx.xx...x)_{2} </math> с <math> 2^k+1 </math> знаками после разделяющей точки и <math> z \le 2 </math> . При помощи программы быстрого умножения точно вычислить <math> z^2=(xx.xx...x)_{2} </math> . После этого точно вычислить <math> V_{k}z^2 </math>, где <math> V_{k}= (0.v_{1}v_{2}...v_{2^{k+1}+3})_{2} </math> . Затем присвоить <math> z \leftarrow 2z-V_{k}z^2+r </math>, где <math> r </math> , удовлетворяющее неравенству <math> 0 \le r <2^{-2^{k+1}-1} </math> , прибавляется при необходимости для округления <math> z </math>, чтобы <math> z </math> было кратным <math> 2^{-2^{k+1}-1} </math> . И наконец присвоить <math> k \leftarrow k+1 </math> .
R3 Если <math> 2^k<n </math> , то вернуться к шагу R2; в противном случае выполнение алгоритма заканчивается.

Литература

• Donald E. Knuth, «The Art of Computer Programming», volume 2, «Seminumerical Algorithms», 3rd edition, Addison-Wesley, 1998
• Dan Zuras, «On Squaring and Multiplying Large Integers», ARITH-11: IEEE Symposium on Computer Arithmetic, 1993, pp. 260 to 271.
• ДАН СССР 150 (1963), 496—498
• Richard P. Brent and Paul Zimmermann, Modern Computer Arithmetic
• Электронные средства и системы управления : Материалы докладов Международной научно-практической конференции (13-16 октября 2010 г.). — Томск: В-Спектр, 2011: В 2 ч. — [www.tusur.ru/export/sites/ru.tusur.new/ru/science/events/conferences/archive/2010-2.pdf Ч. 2.] — 178 с. ISBN 978-5-91191-223-6, С.123-129

Отрывок, характеризующий Длинная арифметика

Наташа вдруг остановилась.
– Дурак! – закричала она на брата, подбежала к стулу, упала на него и зарыдала так, что долго потом не могла остановиться.
– Ничего, маменька, право ничего, так: Петя испугал меня, – говорила она, стараясь улыбаться, но слезы всё текли и всхлипывания сдавливали горло.
Наряженные дворовые, медведи, турки, трактирщики, барыни, страшные и смешные, принеся с собою холод и веселье, сначала робко жались в передней; потом, прячась один за другого, вытеснялись в залу; и сначала застенчиво, а потом всё веселее и дружнее начались песни, пляски, хоровые и святочные игры. Графиня, узнав лица и посмеявшись на наряженных, ушла в гостиную. Граф Илья Андреич с сияющей улыбкой сидел в зале, одобряя играющих. Молодежь исчезла куда то.
Через полчаса в зале между другими ряжеными появилась еще старая барыня в фижмах – это был Николай. Турчанка был Петя. Паяс – это был Диммлер, гусар – Наташа и черкес – Соня, с нарисованными пробочными усами и бровями.
После снисходительного удивления, неузнавания и похвал со стороны не наряженных, молодые люди нашли, что костюмы так хороши, что надо было их показать еще кому нибудь.
Николай, которому хотелось по отличной дороге прокатить всех на своей тройке, предложил, взяв с собой из дворовых человек десять наряженных, ехать к дядюшке.
– Нет, ну что вы его, старика, расстроите! – сказала графиня, – да и негде повернуться у него. Уж ехать, так к Мелюковым.
Мелюкова была вдова с детьми разнообразного возраста, также с гувернантками и гувернерами, жившая в четырех верстах от Ростовых.
– Вот, ma chere, умно, – подхватил расшевелившийся старый граф. – Давай сейчас наряжусь и поеду с вами. Уж я Пашету расшевелю.
Но графиня не согласилась отпустить графа: у него все эти дни болела нога. Решили, что Илье Андреевичу ехать нельзя, а что ежели Луиза Ивановна (m me Schoss) поедет, то барышням можно ехать к Мелюковой. Соня, всегда робкая и застенчивая, настоятельнее всех стала упрашивать Луизу Ивановну не отказать им.
Наряд Сони был лучше всех. Ее усы и брови необыкновенно шли к ней. Все говорили ей, что она очень хороша, и она находилась в несвойственном ей оживленно энергическом настроении. Какой то внутренний голос говорил ей, что нынче или никогда решится ее судьба, и она в своем мужском платье казалась совсем другим человеком. Луиза Ивановна согласилась, и через полчаса четыре тройки с колокольчиками и бубенчиками, визжа и свистя подрезами по морозному снегу, подъехали к крыльцу.
Наташа первая дала тон святочного веселья, и это веселье, отражаясь от одного к другому, всё более и более усиливалось и дошло до высшей степени в то время, когда все вышли на мороз, и переговариваясь, перекликаясь, смеясь и крича, расселись в сани.
Две тройки были разгонные, третья тройка старого графа с орловским рысаком в корню; четвертая собственная Николая с его низеньким, вороным, косматым коренником. Николай в своем старушечьем наряде, на который он надел гусарский, подпоясанный плащ, стоял в середине своих саней, подобрав вожжи.
Было так светло, что он видел отблескивающие на месячном свете бляхи и глаза лошадей, испуганно оглядывавшихся на седоков, шумевших под темным навесом подъезда.
В сани Николая сели Наташа, Соня, m me Schoss и две девушки. В сани старого графа сели Диммлер с женой и Петя; в остальные расселись наряженные дворовые.
– Пошел вперед, Захар! – крикнул Николай кучеру отца, чтобы иметь случай перегнать его на дороге.
Тройка старого графа, в которую сел Диммлер и другие ряженые, визжа полозьями, как будто примерзая к снегу, и побрякивая густым колокольцом, тронулась вперед. Пристяжные жались на оглобли и увязали, выворачивая как сахар крепкий и блестящий снег.
Николай тронулся за первой тройкой; сзади зашумели и завизжали остальные. Сначала ехали маленькой рысью по узкой дороге. Пока ехали мимо сада, тени от оголенных деревьев ложились часто поперек дороги и скрывали яркий свет луны, но как только выехали за ограду, алмазно блестящая, с сизым отблеском, снежная равнина, вся облитая месячным сиянием и неподвижная, открылась со всех сторон. Раз, раз, толконул ухаб в передних санях; точно так же толконуло следующие сани и следующие и, дерзко нарушая закованную тишину, одни за другими стали растягиваться сани.
– След заячий, много следов! – прозвучал в морозном скованном воздухе голос Наташи.
– Как видно, Nicolas! – сказал голос Сони. – Николай оглянулся на Соню и пригнулся, чтоб ближе рассмотреть ее лицо. Какое то совсем новое, милое, лицо, с черными бровями и усами, в лунном свете, близко и далеко, выглядывало из соболей.
«Это прежде была Соня», подумал Николай. Он ближе вгляделся в нее и улыбнулся.
– Вы что, Nicolas?
– Ничего, – сказал он и повернулся опять к лошадям.
Выехав на торную, большую дорогу, примасленную полозьями и всю иссеченную следами шипов, видными в свете месяца, лошади сами собой стали натягивать вожжи и прибавлять ходу. Левая пристяжная, загнув голову, прыжками подергивала свои постромки. Коренной раскачивался, поводя ушами, как будто спрашивая: «начинать или рано еще?» – Впереди, уже далеко отделившись и звеня удаляющимся густым колокольцом, ясно виднелась на белом снегу черная тройка Захара. Слышны были из его саней покрикиванье и хохот и голоса наряженных.
– Ну ли вы, разлюбезные, – крикнул Николай, с одной стороны подергивая вожжу и отводя с кнутом pуку. И только по усилившемуся как будто на встречу ветру, и по подергиванью натягивающих и всё прибавляющих скоку пристяжных, заметно было, как шибко полетела тройка. Николай оглянулся назад. С криком и визгом, махая кнутами и заставляя скакать коренных, поспевали другие тройки. Коренной стойко поколыхивался под дугой, не думая сбивать и обещая еще и еще наддать, когда понадобится.
Николай догнал первую тройку. Они съехали с какой то горы, выехали на широко разъезженную дорогу по лугу около реки.
«Где это мы едем?» подумал Николай. – «По косому лугу должно быть. Но нет, это что то новое, чего я никогда не видал. Это не косой луг и не Дёмкина гора, а это Бог знает что такое! Это что то новое и волшебное. Ну, что бы там ни было!» И он, крикнув на лошадей, стал объезжать первую тройку.
Захар сдержал лошадей и обернул свое уже объиндевевшее до бровей лицо.
Николай пустил своих лошадей; Захар, вытянув вперед руки, чмокнул и пустил своих.
– Ну держись, барин, – проговорил он. – Еще быстрее рядом полетели тройки, и быстро переменялись ноги скачущих лошадей. Николай стал забирать вперед. Захар, не переменяя положения вытянутых рук, приподнял одну руку с вожжами.
– Врешь, барин, – прокричал он Николаю. Николай в скок пустил всех лошадей и перегнал Захара. Лошади засыпали мелким, сухим снегом лица седоков, рядом с ними звучали частые переборы и путались быстро движущиеся ноги, и тени перегоняемой тройки. Свист полозьев по снегу и женские взвизги слышались с разных сторон.
Опять остановив лошадей, Николай оглянулся кругом себя. Кругом была всё та же пропитанная насквозь лунным светом волшебная равнина с рассыпанными по ней звездами.
«Захар кричит, чтобы я взял налево; а зачем налево? думал Николай. Разве мы к Мелюковым едем, разве это Мелюковка? Мы Бог знает где едем, и Бог знает, что с нами делается – и очень странно и хорошо то, что с нами делается». Он оглянулся в сани.
– Посмотри, у него и усы и ресницы, всё белое, – сказал один из сидевших странных, хорошеньких и чужих людей с тонкими усами и бровями.
«Этот, кажется, была Наташа, подумал Николай, а эта m me Schoss; а может быть и нет, а это черкес с усами не знаю кто, но я люблю ее».
– Не холодно ли вам? – спросил он. Они не отвечали и засмеялись. Диммлер из задних саней что то кричал, вероятно смешное, но нельзя было расслышать, что он кричал.
– Да, да, – смеясь отвечали голоса.
– Однако вот какой то волшебный лес с переливающимися черными тенями и блестками алмазов и с какой то анфиладой мраморных ступеней, и какие то серебряные крыши волшебных зданий, и пронзительный визг каких то зверей. «А ежели и в самом деле это Мелюковка, то еще страннее то, что мы ехали Бог знает где, и приехали в Мелюковку», думал Николай.
Действительно это была Мелюковка, и на подъезд выбежали девки и лакеи со свечами и радостными лицами.
– Кто такой? – спрашивали с подъезда.
– Графские наряженные, по лошадям вижу, – отвечали голоса.


Пелагея Даниловна Мелюкова, широкая, энергическая женщина, в очках и распашном капоте, сидела в гостиной, окруженная дочерьми, которым она старалась не дать скучать. Они тихо лили воск и смотрели на тени выходивших фигур, когда зашумели в передней шаги и голоса приезжих.
Гусары, барыни, ведьмы, паясы, медведи, прокашливаясь и обтирая заиндевевшие от мороза лица в передней, вошли в залу, где поспешно зажигали свечи. Паяц – Диммлер с барыней – Николаем открыли пляску. Окруженные кричавшими детьми, ряженые, закрывая лица и меняя голоса, раскланивались перед хозяйкой и расстанавливались по комнате.
– Ах, узнать нельзя! А Наташа то! Посмотрите, на кого она похожа! Право, напоминает кого то. Эдуард то Карлыч как хорош! Я не узнала. Да как танцует! Ах, батюшки, и черкес какой то; право, как идет Сонюшке. Это еще кто? Ну, утешили! Столы то примите, Никита, Ваня. А мы так тихо сидели!
– Ха ха ха!… Гусар то, гусар то! Точно мальчик, и ноги!… Я видеть не могу… – слышались голоса.
Наташа, любимица молодых Мелюковых, с ними вместе исчезла в задние комнаты, куда была потребована пробка и разные халаты и мужские платья, которые в растворенную дверь принимали от лакея оголенные девичьи руки. Через десять минут вся молодежь семейства Мелюковых присоединилась к ряженым.
Пелагея Даниловна, распорядившись очисткой места для гостей и угощениями для господ и дворовых, не снимая очков, с сдерживаемой улыбкой, ходила между ряжеными, близко глядя им в лица и никого не узнавая. Она не узнавала не только Ростовых и Диммлера, но и никак не могла узнать ни своих дочерей, ни тех мужниных халатов и мундиров, которые были на них.
– А это чья такая? – говорила она, обращаясь к своей гувернантке и глядя в лицо своей дочери, представлявшей казанского татарина. – Кажется, из Ростовых кто то. Ну и вы, господин гусар, в каком полку служите? – спрашивала она Наташу. – Турке то, турке пастилы подай, – говорила она обносившему буфетчику: – это их законом не запрещено.
Иногда, глядя на странные, но смешные па, которые выделывали танцующие, решившие раз навсегда, что они наряженные, что никто их не узнает и потому не конфузившиеся, – Пелагея Даниловна закрывалась платком, и всё тучное тело ее тряслось от неудержимого доброго, старушечьего смеха. – Сашинет то моя, Сашинет то! – говорила она.
После русских плясок и хороводов Пелагея Даниловна соединила всех дворовых и господ вместе, в один большой круг; принесли кольцо, веревочку и рублик, и устроились общие игры.
Через час все костюмы измялись и расстроились. Пробочные усы и брови размазались по вспотевшим, разгоревшимся и веселым лицам. Пелагея Даниловна стала узнавать ряженых, восхищалась тем, как хорошо были сделаны костюмы, как шли они особенно к барышням, и благодарила всех за то, что так повеселили ее. Гостей позвали ужинать в гостиную, а в зале распорядились угощением дворовых.
– Нет, в бане гадать, вот это страшно! – говорила за ужином старая девушка, жившая у Мелюковых.
– Отчего же? – спросила старшая дочь Мелюковых.
– Да не пойдете, тут надо храбрость…
– Я пойду, – сказала Соня.
– Расскажите, как это было с барышней? – сказала вторая Мелюкова.
– Да вот так то, пошла одна барышня, – сказала старая девушка, – взяла петуха, два прибора – как следует, села. Посидела, только слышит, вдруг едет… с колокольцами, с бубенцами подъехали сани; слышит, идет. Входит совсем в образе человеческом, как есть офицер, пришел и сел с ней за прибор.
– А! А!… – закричала Наташа, с ужасом выкатывая глаза.
– Да как же, он так и говорит?
– Да, как человек, всё как должно быть, и стал, и стал уговаривать, а ей бы надо занять его разговором до петухов; а она заробела; – только заробела и закрылась руками. Он ее и подхватил. Хорошо, что тут девушки прибежали…
– Ну, что пугать их! – сказала Пелагея Даниловна.
– Мамаша, ведь вы сами гадали… – сказала дочь.
– А как это в амбаре гадают? – спросила Соня.
– Да вот хоть бы теперь, пойдут к амбару, да и слушают. Что услышите: заколачивает, стучит – дурно, а пересыпает хлеб – это к добру; а то бывает…
– Мама расскажите, что с вами было в амбаре?
Пелагея Даниловна улыбнулась.
– Да что, я уж забыла… – сказала она. – Ведь вы никто не пойдете?
– Нет, я пойду; Пепагея Даниловна, пустите меня, я пойду, – сказала Соня.
– Ну что ж, коли не боишься.
– Луиза Ивановна, можно мне? – спросила Соня.
Играли ли в колечко, в веревочку или рублик, разговаривали ли, как теперь, Николай не отходил от Сони и совсем новыми глазами смотрел на нее. Ему казалось, что он нынче только в первый раз, благодаря этим пробочным усам, вполне узнал ее. Соня действительно этот вечер была весела, оживлена и хороша, какой никогда еще не видал ее Николай.
«Так вот она какая, а я то дурак!» думал он, глядя на ее блестящие глаза и счастливую, восторженную, из под усов делающую ямочки на щеках, улыбку, которой он не видал прежде.
– Я ничего не боюсь, – сказала Соня. – Можно сейчас? – Она встала. Соне рассказали, где амбар, как ей молча стоять и слушать, и подали ей шубку. Она накинула ее себе на голову и взглянула на Николая.
«Что за прелесть эта девочка!» подумал он. «И об чем я думал до сих пор!»
Соня вышла в коридор, чтобы итти в амбар. Николай поспешно пошел на парадное крыльцо, говоря, что ему жарко. Действительно в доме было душно от столпившегося народа.
На дворе был тот же неподвижный холод, тот же месяц, только было еще светлее. Свет был так силен и звезд на снеге было так много, что на небо не хотелось смотреть, и настоящих звезд было незаметно. На небе было черно и скучно, на земле было весело.
«Дурак я, дурак! Чего ждал до сих пор?» подумал Николай и, сбежав на крыльцо, он обошел угол дома по той тропинке, которая вела к заднему крыльцу. Он знал, что здесь пойдет Соня. На половине дороги стояли сложенные сажени дров, на них был снег, от них падала тень; через них и с боку их, переплетаясь, падали тени старых голых лип на снег и дорожку. Дорожка вела к амбару. Рубленная стена амбара и крыша, покрытая снегом, как высеченная из какого то драгоценного камня, блестели в месячном свете. В саду треснуло дерево, и опять всё совершенно затихло. Грудь, казалось, дышала не воздухом, а какой то вечно молодой силой и радостью.
С девичьего крыльца застучали ноги по ступенькам, скрыпнуло звонко на последней, на которую был нанесен снег, и голос старой девушки сказал:
– Прямо, прямо, вот по дорожке, барышня. Только не оглядываться.
– Я не боюсь, – отвечал голос Сони, и по дорожке, по направлению к Николаю, завизжали, засвистели в тоненьких башмачках ножки Сони.
Соня шла закутавшись в шубку. Она была уже в двух шагах, когда увидала его; она увидала его тоже не таким, каким она знала и какого всегда немножко боялась. Он был в женском платье со спутанными волосами и с счастливой и новой для Сони улыбкой. Соня быстро подбежала к нему.
«Совсем другая, и всё та же», думал Николай, глядя на ее лицо, всё освещенное лунным светом. Он продел руки под шубку, прикрывавшую ее голову, обнял, прижал к себе и поцеловал в губы, над которыми были усы и от которых пахло жженой пробкой. Соня в самую середину губ поцеловала его и, выпростав маленькие руки, с обеих сторон взяла его за щеки.
– Соня!… Nicolas!… – только сказали они. Они подбежали к амбару и вернулись назад каждый с своего крыльца.


Когда все поехали назад от Пелагеи Даниловны, Наташа, всегда всё видевшая и замечавшая, устроила так размещение, что Луиза Ивановна и она сели в сани с Диммлером, а Соня села с Николаем и девушками.
Николай, уже не перегоняясь, ровно ехал в обратный путь, и всё вглядываясь в этом странном, лунном свете в Соню, отыскивал при этом всё переменяющем свете, из под бровей и усов свою ту прежнюю и теперешнюю Соню, с которой он решил уже никогда не разлучаться. Он вглядывался, и когда узнавал всё ту же и другую и вспоминал, слышав этот запах пробки, смешанный с чувством поцелуя, он полной грудью вдыхал в себя морозный воздух и, глядя на уходящую землю и блестящее небо, он чувствовал себя опять в волшебном царстве.
– Соня, тебе хорошо? – изредка спрашивал он.
– Да, – отвечала Соня. – А тебе ?
На середине дороги Николай дал подержать лошадей кучеру, на минутку подбежал к саням Наташи и стал на отвод.
– Наташа, – сказал он ей шопотом по французски, – знаешь, я решился насчет Сони.
– Ты ей сказал? – спросила Наташа, вся вдруг просияв от радости.
– Ах, какая ты странная с этими усами и бровями, Наташа! Ты рада?
– Я так рада, так рада! Я уж сердилась на тебя. Я тебе не говорила, но ты дурно с ней поступал. Это такое сердце, Nicolas. Как я рада! Я бываю гадкая, но мне совестно было быть одной счастливой без Сони, – продолжала Наташа. – Теперь я так рада, ну, беги к ней.
– Нет, постой, ах какая ты смешная! – сказал Николай, всё всматриваясь в нее, и в сестре тоже находя что то новое, необыкновенное и обворожительно нежное, чего он прежде не видал в ней. – Наташа, что то волшебное. А?
– Да, – отвечала она, – ты прекрасно сделал.
«Если б я прежде видел ее такою, какою она теперь, – думал Николай, – я бы давно спросил, что сделать и сделал бы всё, что бы она ни велела, и всё бы было хорошо».
– Так ты рада, и я хорошо сделал?
– Ах, так хорошо! Я недавно с мамашей поссорилась за это. Мама сказала, что она тебя ловит. Как это можно говорить? Я с мама чуть не побранилась. И никому никогда не позволю ничего дурного про нее сказать и подумать, потому что в ней одно хорошее.
– Так хорошо? – сказал Николай, еще раз высматривая выражение лица сестры, чтобы узнать, правда ли это, и, скрыпя сапогами, он соскочил с отвода и побежал к своим саням. Всё тот же счастливый, улыбающийся черкес, с усиками и блестящими глазами, смотревший из под собольего капора, сидел там, и этот черкес был Соня, и эта Соня была наверное его будущая, счастливая и любящая жена.
Приехав домой и рассказав матери о том, как они провели время у Мелюковых, барышни ушли к себе. Раздевшись, но не стирая пробочных усов, они долго сидели, разговаривая о своем счастьи. Они говорили о том, как они будут жить замужем, как их мужья будут дружны и как они будут счастливы.
На Наташином столе стояли еще с вечера приготовленные Дуняшей зеркала. – Только когда всё это будет? Я боюсь, что никогда… Это было бы слишком хорошо! – сказала Наташа вставая и подходя к зеркалам.
– Садись, Наташа, может быть ты увидишь его, – сказала Соня. Наташа зажгла свечи и села. – Какого то с усами вижу, – сказала Наташа, видевшая свое лицо.
– Не надо смеяться, барышня, – сказала Дуняша.
Наташа нашла с помощью Сони и горничной положение зеркалу; лицо ее приняло серьезное выражение, и она замолкла. Долго она сидела, глядя на ряд уходящих свечей в зеркалах, предполагая (соображаясь с слышанными рассказами) то, что она увидит гроб, то, что увидит его, князя Андрея, в этом последнем, сливающемся, смутном квадрате. Но как ни готова она была принять малейшее пятно за образ человека или гроба, она ничего не видала. Она часто стала мигать и отошла от зеркала.
– Отчего другие видят, а я ничего не вижу? – сказала она. – Ну садись ты, Соня; нынче непременно тебе надо, – сказала она. – Только за меня… Мне так страшно нынче!
Соня села за зеркало, устроила положение, и стала смотреть.
– Вот Софья Александровна непременно увидят, – шопотом сказала Дуняша; – а вы всё смеетесь.
Соня слышала эти слова, и слышала, как Наташа шопотом сказала:
– И я знаю, что она увидит; она и прошлого года видела.
Минуты три все молчали. «Непременно!» прошептала Наташа и не докончила… Вдруг Соня отсторонила то зеркало, которое она держала, и закрыла глаза рукой.
– Ах, Наташа! – сказала она.
– Видела? Видела? Что видела? – вскрикнула Наташа, поддерживая зеркало.
Соня ничего не видала, она только что хотела замигать глазами и встать, когда услыхала голос Наташи, сказавшей «непременно»… Ей не хотелось обмануть ни Дуняшу, ни Наташу, и тяжело было сидеть. Она сама не знала, как и вследствие чего у нее вырвался крик, когда она закрыла глаза рукою.
– Его видела? – спросила Наташа, хватая ее за руку.
– Да. Постой… я… видела его, – невольно сказала Соня, еще не зная, кого разумела Наташа под словом его: его – Николая или его – Андрея.
«Но отчего же мне не сказать, что я видела? Ведь видят же другие! И кто же может уличить меня в том, что я видела или не видала?» мелькнуло в голове Сони.
– Да, я его видела, – сказала она.
– Как же? Как же? Стоит или лежит?
– Нет, я видела… То ничего не было, вдруг вижу, что он лежит.
– Андрей лежит? Он болен? – испуганно остановившимися глазами глядя на подругу, спрашивала Наташа.
– Нет, напротив, – напротив, веселое лицо, и он обернулся ко мне, – и в ту минуту как она говорила, ей самой казалось, что она видела то, что говорила.
– Ну а потом, Соня?…
– Тут я не рассмотрела, что то синее и красное…
– Соня! когда он вернется? Когда я увижу его! Боже мой, как я боюсь за него и за себя, и за всё мне страшно… – заговорила Наташа, и не отвечая ни слова на утешения Сони, легла в постель и долго после того, как потушили свечу, с открытыми глазами, неподвижно лежала на постели и смотрела на морозный, лунный свет сквозь замерзшие окна.


Вскоре после святок Николай объявил матери о своей любви к Соне и о твердом решении жениться на ней. Графиня, давно замечавшая то, что происходило между Соней и Николаем, и ожидавшая этого объяснения, молча выслушала его слова и сказала сыну, что он может жениться на ком хочет; но что ни она, ни отец не дадут ему благословения на такой брак. В первый раз Николай почувствовал, что мать недовольна им, что несмотря на всю свою любовь к нему, она не уступит ему. Она, холодно и не глядя на сына, послала за мужем; и, когда он пришел, графиня хотела коротко и холодно в присутствии Николая сообщить ему в чем дело, но не выдержала: заплакала слезами досады и вышла из комнаты. Старый граф стал нерешительно усовещивать Николая и просить его отказаться от своего намерения. Николай отвечал, что он не может изменить своему слову, и отец, вздохнув и очевидно смущенный, весьма скоро перервал свою речь и пошел к графине. При всех столкновениях с сыном, графа не оставляло сознание своей виноватости перед ним за расстройство дел, и потому он не мог сердиться на сына за отказ жениться на богатой невесте и за выбор бесприданной Сони, – он только при этом случае живее вспоминал то, что, ежели бы дела не были расстроены, нельзя было для Николая желать лучшей жены, чем Соня; и что виновен в расстройстве дел только один он с своим Митенькой и с своими непреодолимыми привычками.