Метод Ньютона

Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Модификацией метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.

Описание метода

Обоснование

Чтобы численно решить уравнение <math>f(x)=0</math> методом простой итерации, его необходимо привести к эквивалентному уравнению: <math>x=\varphi(x)</math>, где <math>\varphi</math> — сжимающее отображение.

Для наилучшей сходимости метода в точке очередного приближения <math>x^*</math> должно выполняться условие <math>\varphi'(x^*)=0</math>. Решение данного уравнения ищут в виде <math>\varphi(x)=x+\alpha(x)f(x)</math>, тогда:

<math>\varphi'(x^*)=1+\alpha'(x^*)f(x^*)+\alpha(x^*) f'(x^*)=0.</math>

В предположении, что точка приближения «достаточно близка» к корню <math>\tilde{x}</math>, и что заданная функция непрерывна <math>(f(x^*)\approx f(\tilde{x})=0)</math>, окончательная формула для <math>\alpha(x)</math> такова:

<math>\alpha(x)=-\frac{1}{f'(x)}.</math>

С учётом этого функция <math>\varphi(x)</math> определяется:

<math>\varphi(x)=x-\frac{f(x)}{f'(x)}.</math>

При некоторых условиях эта функция в окрестности корня осуществляет сжимающее отображение, и алгоритм нахождения численного решения уравнения <math>f(x)=0</math> сводится к итерационной процедуре вычисления:

<math>x_{n+1}=x_{n}-\frac{f(x_n)}{f'(x_n)}.</math>

По теореме Банаха последовательность приближений стремится к корню уравнения <math>f(x)=0</math>.

Геометрическая интерпретация

Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к графику исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.

Пусть 1) вещественнозначная функция <math>f(x)\colon(a,\,b)\to\R</math> непрерывно дифференцируема на интервале <math>(a,\,b)</math> ;
2) существует искомая точка <math>x^{*}\in (a,\,b)</math> : <math>f(x^{*})= 0</math> ;
3) существуют <math>C > 0</math> и <math>\delta > 0</math> такие, что
<math>\vert f'(x) \vert \ge C</math> для <math>x\in(a,\,x^{*}-\delta ] \cup [ x^{*}+\delta,\,b)</math>
и <math>f'(x)\ne 0</math> для <math>x\in(x^{*}-\delta,\, x^{*})\cup(x^{*},\, x^{*}+\delta )</math> ;
4) точка <math>x_n \in (a,\,b)</math> такова, что <math>f(x_n)\ne 0</math> .
Тогда формула итеративного приближения <math>x_n</math> к <math>x^{*}</math> может быть выведена из геометрического смысла касательной следующим образом:

<math>f'(x_n)=\mathrm{tg}\,\alpha_{n} = \frac{\Delta y}{\Delta x} = \frac{f(x_n)-0}{x_n-x_{n+1}} = \frac{0-f(x_n)}{x_{n+1}-x_n},</math>

где <math>\alpha_{n}</math> — угол наклона касательной прямой <math>y(x)=f(x_n) + (x - x_n) \cdot \mathrm{tg}\,\alpha_{n}</math> к графику <math>f</math> в точке <math>(x_n;f(x_n))</math> .

Следовательно ( в уравнении касательной прямой полагаем <math>y(x_{n+1})=0</math> ) искомое выражение для <math>x_{n+1}</math> имеет вид :

<math>x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}.</math>

Если <math>x_{n+1} \in (a,\,b)</math>, то это значение можно использовать в качестве следующего приближения к <math>x^{*}</math> .

Если <math>x_{n+1} \notin (a,\,b)</math>, то имеет место «перелёт» (корень <math>x^{*}</math> лежит рядом с границей <math>(a,\,b)</math>). В этом случае надо (воспользовавшись идеей метода половинного деления) заменять <math>x_{n+1}</math> на <math>\frac{x_{n}+x_{n+1}}{2}</math> до тех пор, пока точка «не вернётся» в область поиска <math>(a,\,b)</math> .

Замечания. 1) Наличие непрерывной производной даёт возможность строить непрерывно меняющуюся касательную на всей области поиска решения <math>(a,\,b)\;</math> .
2) Случаи граничного (в точке <math>a</math> или в точке <math>b</math>) расположения искомого решения <math>x^{*}</math> рассматриваются аналогичным образом.
3) С геометрической точки зрения равенство <math>f'(x_n)= 0</math> означает, что касательная прямая к графику <math>f</math> в точке <math>(x_n;f(x_n))</math> - параллельна оси <math>OX</math> и при <math>f(x_n)\ne 0</math> не пересекается с ней в конечной части.
4) Чем больше константа <math>C > 0</math> и чем меньше константа <math>\delta > 0</math> из пункта 3 условий, тем для <math>x_{n}\in(a,\,x^{*}-\delta ] \cup [ x^{*}+\delta,\,b)</math> пересечение касательной к графику <math>f</math> и оси <math>OX</math> ближе к точке <math>(x^{*};\;0)</math> , т.е. тем ближе значение <math>x_{n+1}</math> к искомой <math>x^{*}\in (a,\,b)</math> .

Итерационный процесс начинается с некоторого начального приближения <math>x_0 \in (a,\,b)</math> , причём между <math>x_0 \in (a,\,b)</math> и искомой точкой <math>x^{*}\in (a,\,b)</math> не должно быть других нулей функции <math>f</math> , т.е. «чем ближе <math>x_0</math> к искомому корню <math>x^{*}</math> , тем лучше». Если предположения о нахождении <math>x^{*}</math> отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях.

Для предварительно заданных <math>\varepsilon_{x} >0</math> , <math>\varepsilon_{f} >0</math> итерационный процесс завершается если <math>\left \vert \frac{f(x_n)}{f'(x_n)} \right \vert \approx \vert x_{n+1}-x_n \vert <\varepsilon_{x}</math> и <math> \vert f(x_{n+1})\vert <\varepsilon_{f}</math> .
В частности, для матрицы дисплея <math>\varepsilon_{x}</math> и <math>\varepsilon_{f}</math> могут быть рассчитаны, исходя из масштаба отображения графика <math>f</math> , т.е. если <math>x_n</math> и <math>x_{n+1}</math> попадают в один вертикальный, а <math>f(x_n)</math> и <math>f(x_{n+1})</math> в один горизонтальный ряд.

Алгоритм

1. Задается начальное приближение <math>x_0</math>.
2. Пока не выполнено условие остановки, в качестве которого можно взять <math>|x_{n+1}-x_n|<\varepsilon</math> или <math>|f(x_{n+1})|<\varepsilon</math> (то есть погрешность в нужных пределах), вычисляют новое приближение: <math>x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}</math>.

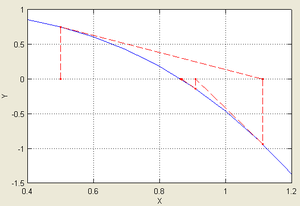
Пример

Иллюстрация применения метода Ньютона к функции <math>f(x)=\cos x-x^3</math> с начальным приближением в точке <math>x_0=0{,}5</math>.
Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум.

Рассмотрим задачу о нахождении положительных <math>x</math>, для которых <math>\cos x=x^3</math>. Эта задача может быть представлена как задача нахождения нуля функции <math>f(x)=\cos x-x^3</math>. Имеем выражение для производной <math>f'(x)=-\sin x-3x^2</math>. Так как <math>\cos x\leqslant 1</math> для всех <math>x</math> и <math>x^3>1</math> для <math>x>1</math>, очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение <math>x_0 = 0{,}5</math>, тогда:

<math>\begin{matrix}

x_1 & = & x_0-\dfrac{f(x_0)}{f'(x_0)} & = & 1{,}112\;141\;637\;097, \\ x_2 & = & x_1-\dfrac{f(x_1)}{f'(x_1)} & = & \underline{0{,}}909\;672\;693\;736, \\ x_3 & = & x_2-\dfrac{f(x_2)}{f'(x_2)} & = & \underline{0{,}86}7\;263\;818\;209, \\ x_4 & = & x_3-\dfrac{f(x_3)}{f'(x_3)} & = & \underline{0{,}865\;47}7\;135\;298, \\ x_5 & = & x_4-\dfrac{f(x_4)}{f'(x_4)} & = & \underline{0{,}865\;474\;033\;1}11, \\ x_6 & = & x_5-\dfrac{f(x_5)}{f'(x_5)} & = & \underline{0{,}865\;474\;033\;102}. \end{matrix}</math> Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.

Условия применения

Рассмотрим ряд примеров, указывающих на недостатки метода.

Контрпримеры

• Если начальное приближение недостаточно близко к решению, то метод может не сойтись.

Пусть

<math>f(x)=x^3-2x+2.</math>

Тогда

<math>x_{n+1}=x_{n}-\frac{x_n^3-2x_n+2}{3x_n^2-2}.</math>

Возьмём нуль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст нуль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.

• Если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня.

Рассмотрим функцию:

<math>f(x)=\begin{cases}

x, & x=0, \\ x+x^2\sin\left(\dfrac{2}{x}\right), & x\neq 0. \end{cases}</math> Тогда <math>f'(0)=1</math> и <math>f'(x)=1+2x\sin(2/x)-2\cos(2/x)</math> всюду, кроме 0.

В окрестности корня производная меняет знак при приближении <math>x</math> к нулю справа или слева. В то время, как <math>f(x)\geqslant x-x^2>0</math> для <math>0<x<1</math>.

Таким образом <math>f(x)/f'(x)</math> не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне, <math>f</math> бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.

• Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.

Рассмотрим пример:

<math>f(x)=x+x^{4/3}.</math>

Тогда <math>f'(x)=1+(4/3)x^{1/3}</math> и <math>f(x)=(4/9)x^{-2/3}</math> за исключением <math>x=0</math>, где она не определена.

На очередном шаге имеем <math>x_n</math>:

<math>x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}=\frac{(1/3)x_n^{4/3}}{(1+(4/3)x_n^{1/3})}.</math>

Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и <math>f</math> бесконечно дифференцируема везде, кроме как в корне.

• Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.

Пусть

<math>f(x)=x^2.</math>

Тогда <math>f'(x)=2x</math> и следовательно <math>x-f(x)/f'(x)=x/2</math>. Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.

Ограничения

Пусть задано уравнение <math>f(x)=0</math>, где <math>f(x)\colon\mathbb{X}\to\R</math> и надо найти его решение.

Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).

Теорема Канторовича.

Если существуют такие константы <math>A,\;B,\;C</math>, что:

1. <math>\frac{1}{|f'(x)|}<A</math> на <math>[a,\;b]</math>, то есть <math>f'(x)</math> существует и не равна нулю;
2. <math>\left|\frac{f(x)}{f'(x)}\right|<B</math> на <math>[a,\;b]</math>, то есть <math>f(x)</math> ограничена;
3. <math>\exist f(x)</math> на <math>[a,\;b]</math>, и <math>|f(x)|\leqslant C\leqslant\frac{1}{2AB}</math>;

Причём длина рассматриваемого отрезка <math>|a-b|<\frac{1}{AB}\left(1-\sqrt{1-2ABC}\right)</math>. Тогда справедливы следующие утверждения:

1. на <math>[a,\;b]</math> существует корень <math>x^*</math> уравнения <math>f(x)=0\colon\exist x^*\in[a,\;b]\colon f(x^*)=0</math>;
2. если <math>x_0=\frac{a+b}{2}</math>, то итерационная последовательность сходится к этому корню: <math>\left\{ x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}\right\}\to x^*</math>;
3. погрешность может быть оценена по формуле <math>|x^*-x_n|\leqslant\frac{B}{2^{n-1}}(2ABC)^{2^{n-1}}</math>.

Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:

<math>|x^*-x_n|\leqslant\frac{B}{2^{n-1}}(2ABC)^{2^{n-1}}=\frac{1}{2}\frac{B}{2^{n-2}}\left((2ABC)^{2^{n-2}}\right)^2=\alpha |x^*-x_{n-1}|^2.</math>

Тогда ограничения на исходную функцию <math>f(x)</math> будут выглядеть так:

1. функция должна быть ограничена;
2. функция должна быть гладкой, дважды дифференцируемой;
3. её первая производная <math>f'(x)</math> равномерно отделена от нуля;
4. её вторая производная <math>f(x)</math> должна быть равномерно ограничена.

Историческая справка

Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения <math>x_n</math>, а последовательность полиномов и в результате получал приближённое решение <math>x</math>.

Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений <math>x_n</math> вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.

В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.

Обобщения и модификации

Метод секущих

Родственный метод секущих является «приближённым» методом Ньютона и позволяет не вычислять производную. Значение производной в итерационной формуле заменяется её оценкой по двум предыдущим точкам итераций:

<math>f'(x_n) \approx \frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}</math> .

Таким образом, основная формула имеет вид

<math>x_{n+1} = x_n - f(x_n) \cdot \frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})} .</math>

Этот метод схож с методом Ньютона, но имеет немного меньшую скорость сходимости. Порядок сходимости метода равен золотому сечению — 1,618...

Замечания. 1) Для начала итерационного процесса требуются два различных значения <math>x_0</math> и <math>x_1</math> .
2) В отличие от «настоящего метода Ньютона» (метода касательных), требующего хранить только <math>x_{n}</math> (и в ходе вычислений - временно <math>f(x_{n})</math> и <math>f'(x_{n})</math>), для метода секущих требуется сохранение <math>x_{n-1}</math> , <math>x_{n}</math> , <math>f(x_{n-1})</math> , <math>f(x_{n})</math> .
3) Применяется, если вычисление <math>f'(x)</math> затруднено (например, требует большого количества машинных ресурсов: времени и/или памяти).

Метод одной касательной

В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.

Формула итераций этого метода имеет вид:

<math>x_{n+1}=x_n-\frac{1}{f'(x_0)}f(x_n).</math>

Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения <math>x_0</math>, а затем использовать это значение на каждой последующей итерации:

<math>\alpha(x)=\alpha_0=-\dfrac{1}{f'(x_0)}.</math>

При таком выборе <math>\alpha_0</math> в точке <math>x_0</math> выполнено равенство:

<math>\varphi'(x_0)=1+\alpha_0f'(x_0)=0,</math>

и если отрезок, на котором предполагается наличие корня <math>x^*</math> и выбрано начальное приближение <math>x_0</math>, достаточно мал, а производная <math>\varphi'(x)</math> непрерывна, то значение <math>\varphi'(x^*)</math> будет не сильно отличаться от <math>\varphi'(x_0)=0</math> и, следовательно, график <math> y=\varphi(x)</math> пройдёт почти горизонтально, пересекая прямую <math>y=x</math>, что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.

Этот метод является частным случаем метода простой итерации. Он имеет линейный порядок сходимости.

Многомерный случай

Обобщим полученный результат на многомерный случай.

Пусть необходимо найти решение системы:

<math>\left\{\begin{array}{lcr}

f_1(x_1,\;x_2,\;\ldots,\;x_n) & = & 0, \\ \ldots & & \\ f_n(x_1,\;x_2,\;\ldots,\;x_n) & = & 0. \end{array}\right.</math> Выбирая некоторое начальное значение <math>\vec{x}^{[0]}</math>, последовательные приближения <math>\vec{x}^{[j+1]}</math> находят путём решения систем уравнений:

<math>f_i+\sum_{k=1}^n\frac{\partial f_i}{\partial x_k}(x^{[j+1]}_k-x_k^{[j]})=0,\qquad i=1,\;2,\;\ldots,\;n,</math>

где <math>\vec{x}^{[j]}=(x_1^{[j]},\;x_2^{[j]},\;\ldots,\;x_n^{[j]}),\quad j=0,\;1,\;2,\;\ldots</math>.

Применительно к задачам оптимизации

Пусть необходимо найти минимум функции многих переменных <math>f(\vec{x})\colon\R^n\to\R</math>. Эта задача равносильна задаче нахождения нуля градиента <math>\nabla f(\vec{x})</math>. Применим изложенный выше метод Ньютона:

<math>\nabla f(\vec{x}^{[j]})+H(\vec{x}^{[j]})(\vec{x}^{[j+1]}-\vec{x}^{[j]})=0,\quad j=1,\;2,\;\ldots,\;n,</math>

где <math>H(\vec{x})</math> — гессиан функции <math>f(\vec{x})</math>.

В более удобном итеративном виде это выражение выглядит так:

<math>\vec{x}^{[j+1]}=\vec{x}^{[j]}-H^{-1}(\vec{x}^{[j]})\nabla f(\vec{x}^{[j]}).</math>

Следует отметить, что в случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.

Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.

Метод Ньютона — Рафсона

Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:

<math>\vec{x}^{[j+1]}=\vec{x}^{[j]}-\lambda_j H^{-1}(\vec{x}^{[j]})\nabla f(\vec{x}^{[j]}),</math>

где <math>\lambda_j=\arg\min_\lambda f(\vec{x}^{[j]}-\lambda H^{-1}(\vec{x}^{[j]})\nabla f(\vec{x}^{[j]})).</math> Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением <math>H(f(\vec{x}^{[0]}))</math> и обновляют его лишь раз в <math>m</math> шагов, либо не обновляют вовсе.

Применительно к задачам о наименьших квадратах

На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:

<math>F(\vec{x})=\|\vec{f}(\vec{x})\|=\sum_{i=1}^m f_i^2(\vec{x})=\sum_{i=1}^m (\varphi_i(\vec{x})-\mathcal{F}_i)^2\to\min.</math>

Эти задачи отличаются особым видом градиента и матрицы Гессе:

<math>\nabla F(\vec{x})=2J^T(\vec{x})\vec{f}(\vec{x}),</math>

<math>H(\vec{x})=2J^T(\vec{x})J(\vec{x})+2Q(\vec{x}),\qquad Q(\vec{x})=\sum_{i=1}^m f_i(\vec{x})H_i(\vec{x}),</math>

где <math>J(\vec{x})</math> — матрица Якоби вектор-функции <math>\vec{f}(\vec{x})</math>, <math>H_i(\vec{x})</math> — матрица Гессе для её компоненты <math>f_i(\vec{x})</math>.

Тогда очередное направление <math>\vec{p}</math> определяется из системы:

<math>\left[J^T(\vec{x})J(\vec{x})+\sum_{i=1}^m f_i(\vec{x})H_i(\vec{x})\right]\vec{p}=-J^T(\vec{x})\vec{f}(\vec{x}).</math>

Метод Гаусса — Ньютона

Метод Гаусса — Ньютона строится на предположении о том, что слагаемое <math>J^T(\vec{x})J(\vec{x})</math> доминирует над <math>Q(\vec{x})</math>. Это требование не соблюдается, если минимальные невязки велики, то есть если норма <math>\|\vec{f}(\vec{x})\|</math> сравнима с максимальным собственным значением матрицы <math>J^T(\vec{x})J(\vec{x})</math>. В противном случае можно записать:

<math>J^T(\vec{x})J(\vec{x})\vec{p}=-J^T(\vec{x})\vec{f}(\vec{x}).</math>

Таким образом, когда норма <math>\|Q(\vec{x})\|</math> близка к нулю, а матрица <math>J(\vec{x})</math> имеет полный столбцевой ранг, направление <math>\vec{p}</math> мало отличается от ньютоновского (с учётом <math>Q(\vec{x})</math>), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.

Обобщение на комплексную плоскость

До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексного переменного. При этом процедура остаётся неизменной:

<math>z_{n+1}=z_n-\frac{f(z_n)}{f'(z_n)}.</math>

Особый интерес представляет выбор начального приближения <math>z_0</math>. Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кейли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.

Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.

Реализация

Scala

object NewtonMethod {

  val accuracy = 1e-6

  @tailrec
  def method(x0: Double, f: Double => Double, dfdx: Double => Double, e: Double): Double = {
    val x1 = x0 - f(x0) / dfdx(x0)
    if (abs(x1 - x0) < e) x1
    else method(x1, f, dfdx, e)
  }

  def g(C: Double) = (x: Double) => x*x - C

  def dgdx(x: Double) = 2*x

  def sqrt(x: Double) = x match {
    case 0 => 0
    case x if (x < 0) => Double.NaN
    case x if (x > 0) => method(x/2, g(x), dgdx, accuracy) 
  }
}

Python

def newtons_method(x0, f, f1, e):
    #f1 - производная
    while True:
        x1 = x0 - (f(x0) / f1(x0))
        if abs(x1 - x0) < e:
            return x1
        x0 = x1

PHP

<?php
// PHP 5.4
function newtons_method(
	$a = -1, $b = 1, 
	$f = function($x) {
	
		return pow($x, 4) - 1;
	
	},
	$derivative_f = function($x) {

		return 4 * pow($x, 3);
	
	}, $eps = 1E-3) {

        $xa = $a;
        $xb = $b;

        $iteration = 0;

        while (abs($xb) > $eps) {

            $p1 = $f($xa);
            $q1 = $derivative_f($xa);
            $xa -= $p1 / $q1;
            $xb = $p1;
            ++$iteration;

        }

        return $xa;

}

Octave

function res = nt()
eps = 1e-7;
x0_1 = [-0.5,0.5];
max_iter = 500;
xopt = new(@resh, eps, max_iter);   
xopt
endfunction
function a = new(f, eps, max_iter)
x=-1;
p0=1;
i=0;
 while (abs(p0)>=eps)
[p1,q1]=f(x);
 x=x-p1/q1;
p0=p1;
 i=i+1;
 end
 i
 a=x;
endfunction
function[p,q]= resh(x)   % p= -5*x.^5+4*x.^4-12*x.^3+11*x.^2-2*x+1;
   p=-25*x.^4+16*x.^3-36*x.^2+22*x-2;
   q=-100*x.^3+48*x.^2-72*x+22;
endfunction

С

#include <stdio.h>
#include <math.h>

#define eps 0.000001
double fx(double x) { return x*x-17;}
double dfx(double x) { return 2*x;}

typedef double(*function)(double x);

double solve(function fx, function dfx, double x0) {
  double x1  = x0 - fx(x0)/dfx(x0);
  while (fabs(x1-x0)>eps) {
    x0 = x1;
    x1 = x1 - fx(x1)/dfx(x1);
  }
  return x1;
}

int main () {
  printf("%f\n",solve(fx,dfx,4));
  return 0;
}

C++

typedef double (*function)(double x);

double TangentsMethod(function f, function df, double xn, double eps) {
   double x1  = xn - f(xn)/df(xn);
   double x0 = xn;
   while(abs(x0-x1) > eps) {
      x0 = x1;
      x1 = x1 - f(x1)/df(x1);
   }
   return x1;
}

//Выбор начального приближения
xn = MyFunction(A)*My2Derivative(A) > 0 ? B : A;

double MyFunction(double x) { return (pow(x, 5) - x - 0.2); } //Ваша функция
double MyDerivative(double x) { return (5*pow(x, 4) - 1); } //Первая производная
double My2Derivative(double x) { return (20*pow(x, 3)); } //Вторая производная

//Пример вызова функции
double x = TangentsMethod(MyFunction, MyDerivative, xn, 0.1)

Литература

1. Акулич И. Л. Математическое программирование в примерах и задачах : Учеб. пособие для студентов эконом. спец. вузов. — М. : Высшая школа, 1986. — 319 с. : ил. — ББК 22.1 А44. — УДК [www.google.ru/search?q=удк+517.8&btnG=Искать+книги&tbm=bks&tbo=1&hl=ru 517.8].</span>
2. Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров : Учеб. пособие. — М. : Высшая школа, 1994. — 544 с. : ил. — ББК 32.97 А62. — УДК [www.google.ru/search?q=удк+683.1&btnG=Искать+книги&tbm=bks&tbo=1&hl=ru 683.1]. — ISBN 5-06-000625-5.</span>
3. Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд. — М. : Лаборатория Базовых Знаний, 2000.</span>
4. Вавилов С. И. [vivovoco.astronet.ru/VV/BOOKS/NEWTON/CHAPTER_13.HTM Исаак Ньютон]. — М. : Изд. АН СССР, 1945.</span>
5. Волков Е. А. Численные методы. — М. : Физматлит, 2003.</span>
6. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М. : Мир, 1985.</span>
7. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М. : Наука, 1970. — С. 575-576.</span>
8. Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.</span>
9. Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М. : МИФИ, 1982.</span>
10. Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.</span>

См. также

• Метод простой итерации
• Двоичный поиск
• Метод дихотомии
• Метод секущих
• Метод Мюллера
• Метод хорд
• Фрактал
• Численное решение уравнений

Ссылки

• [fractalworld.xaoc.ru/article/frnew.html «Бассейны Ньютона» на сайте fractalworld.xaoc.ru]
• [www.scottish-wetlands.org/073/73081.htm «Исаак Ньютон» на сайте www.scottish-wetlands.org]
• [math.nsc.ru/LBRT/g2/english/ssk/talk_lvk95.html «Математические работы Канторовича» на сайте Института математики СО РАН]

Отрывок, характеризующий Метод Ньютона

Один ближайший старичок оглянулся на него, но тотчас был отвлечен криком, начавшимся на другой стороне стола.
– Да, Москва будет сдана! Она будет искупительницей! – кричал один.
– Он враг человечества! – кричал другой. – Позвольте мне говорить… Господа, вы меня давите…


В это время быстрыми шагами перед расступившейся толпой дворян, в генеральском мундире, с лентой через плечо, с своим высунутым подбородком и быстрыми глазами, вошел граф Растопчин.
– Государь император сейчас будет, – сказал Растопчин, – я только что оттуда. Я полагаю, что в том положении, в котором мы находимся, судить много нечего. Государь удостоил собрать нас и купечество, – сказал граф Растопчин. – Оттуда польются миллионы (он указал на залу купцов), а наше дело выставить ополчение и не щадить себя… Это меньшее, что мы можем сделать!
Начались совещания между одними вельможами, сидевшими за столом. Все совещание прошло больше чем тихо. Оно даже казалось грустно, когда, после всего прежнего шума, поодиночке были слышны старые голоса, говорившие один: «согласен», другой для разнообразия: «и я того же мнения», и т. д.
Было велено секретарю писать постановление московского дворянства о том, что москвичи, подобно смолянам, жертвуют по десять человек с тысячи и полное обмундирование. Господа заседавшие встали, как бы облегченные, загремели стульями и пошли по зале разминать ноги, забирая кое кого под руку и разговаривая.
– Государь! Государь! – вдруг разнеслось по залам, и вся толпа бросилась к выходу.
По широкому ходу, между стеной дворян, государь прошел в залу. На всех лицах выражалось почтительное и испуганное любопытство. Пьер стоял довольно далеко и не мог вполне расслышать речи государя. Он понял только, по тому, что он слышал, что государь говорил об опасности, в которой находилось государство, и о надеждах, которые он возлагал на московское дворянство. Государю отвечал другой голос, сообщавший о только что состоявшемся постановлении дворянства.
– Господа! – сказал дрогнувший голос государя; толпа зашелестила и опять затихла, и Пьер ясно услыхал столь приятно человеческий и тронутый голос государя, который говорил: – Никогда я не сомневался в усердии русского дворянства. Но в этот день оно превзошло мои ожидания. Благодарю вас от лица отечества. Господа, будем действовать – время всего дороже…
Государь замолчал, толпа стала тесниться вокруг него, и со всех сторон слышались восторженные восклицания.
– Да, всего дороже… царское слово, – рыдая, говорил сзади голос Ильи Андреича, ничего не слышавшего, но все понимавшего по своему.
Из залы дворянства государь прошел в залу купечества. Он пробыл там около десяти минут. Пьер в числе других увидал государя, выходящего из залы купечества со слезами умиления на глазах. Как потом узнали, государь только что начал речь купцам, как слезы брызнули из его глаз, и он дрожащим голосом договорил ее. Когда Пьер увидал государя, он выходил, сопутствуемый двумя купцами. Один был знаком Пьеру, толстый откупщик, другой – голова, с худым, узкобородым, желтым лицом. Оба они плакали. У худого стояли слезы, но толстый откупщик рыдал, как ребенок, и все твердил:
– И жизнь и имущество возьми, ваше величество!
Пьер не чувствовал в эту минуту уже ничего, кроме желания показать, что все ему нипочем и что он всем готов жертвовать. Как упрек ему представлялась его речь с конституционным направлением; он искал случая загладить это. Узнав, что граф Мамонов жертвует полк, Безухов тут же объявил графу Растопчину, что он отдает тысячу человек и их содержание.
Старик Ростов без слез не мог рассказать жене того, что было, и тут же согласился на просьбу Пети и сам поехал записывать его.
На другой день государь уехал. Все собранные дворяне сняли мундиры, опять разместились по домам и клубам и, покряхтывая, отдавали приказания управляющим об ополчении, и удивлялись тому, что они наделали.



Наполеон начал войну с Россией потому, что он не мог не приехать в Дрезден, не мог не отуманиться почестями, не мог не надеть польского мундира, не поддаться предприимчивому впечатлению июньского утра, не мог воздержаться от вспышки гнева в присутствии Куракина и потом Балашева.
Александр отказывался от всех переговоров потому, что он лично чувствовал себя оскорбленным. Барклай де Толли старался наилучшим образом управлять армией для того, чтобы исполнить свой долг и заслужить славу великого полководца. Ростов поскакал в атаку на французов потому, что он не мог удержаться от желания проскакаться по ровному полю. И так точно, вследствие своих личных свойств, привычек, условий и целей, действовали все те неперечислимые лица, участники этой войны. Они боялись, тщеславились, радовались, негодовали, рассуждали, полагая, что они знают то, что они делают, и что делают для себя, а все были непроизвольными орудиями истории и производили скрытую от них, но понятную для нас работу. Такова неизменная судьба всех практических деятелей, и тем не свободнее, чем выше они стоят в людской иерархии.
Теперь деятели 1812 го года давно сошли с своих мест, их личные интересы исчезли бесследно, и одни исторические результаты того времени перед нами.
Но допустим, что должны были люди Европы, под предводительством Наполеона, зайти в глубь России и там погибнуть, и вся противуречащая сама себе, бессмысленная, жестокая деятельность людей – участников этой войны, становится для нас понятною.
Провидение заставляло всех этих людей, стремясь к достижению своих личных целей, содействовать исполнению одного огромного результата, о котором ни один человек (ни Наполеон, ни Александр, ни еще менее кто либо из участников войны) не имел ни малейшего чаяния.
Теперь нам ясно, что было в 1812 м году причиной погибели французской армии. Никто не станет спорить, что причиной погибели французских войск Наполеона было, с одной стороны, вступление их в позднее время без приготовления к зимнему походу в глубь России, а с другой стороны, характер, который приняла война от сожжения русских городов и возбуждения ненависти к врагу в русском народе. Но тогда не только никто не предвидел того (что теперь кажется очевидным), что только этим путем могла погибнуть восьмисоттысячная, лучшая в мире и предводимая лучшим полководцем армия в столкновении с вдвое слабейшей, неопытной и предводимой неопытными полководцами – русской армией; не только никто не предвидел этого, но все усилия со стороны русских были постоянно устремляемы на то, чтобы помешать тому, что одно могло спасти Россию, и со стороны французов, несмотря на опытность и так называемый военный гений Наполеона, были устремлены все усилия к тому, чтобы растянуться в конце лета до Москвы, то есть сделать то самое, что должно было погубить их.
В исторических сочинениях о 1812 м годе авторы французы очень любят говорить о том, как Наполеон чувствовал опасность растяжения своей линии, как он искал сражения, как маршалы его советовали ему остановиться в Смоленске, и приводить другие подобные доводы, доказывающие, что тогда уже будто понята была опасность кампании; а авторы русские еще более любят говорить о том, как с начала кампании существовал план скифской войны заманивания Наполеона в глубь России, и приписывают этот план кто Пфулю, кто какому то французу, кто Толю, кто самому императору Александру, указывая на записки, проекты и письма, в которых действительно находятся намеки на этот образ действий. Но все эти намеки на предвидение того, что случилось, как со стороны французов так и со стороны русских выставляются теперь только потому, что событие оправдало их. Ежели бы событие не совершилось, то намеки эти были бы забыты, как забыты теперь тысячи и миллионы противоположных намеков и предположений, бывших в ходу тогда, но оказавшихся несправедливыми и потому забытых. Об исходе каждого совершающегося события всегда бывает так много предположений, что, чем бы оно ни кончилось, всегда найдутся люди, которые скажут: «Я тогда еще сказал, что это так будет», забывая совсем, что в числе бесчисленных предположений были делаемы и совершенно противоположные.
Предположения о сознании Наполеоном опасности растяжения линии и со стороны русских – о завлечении неприятеля в глубь России – принадлежат, очевидно, к этому разряду, и историки только с большой натяжкой могут приписывать такие соображения Наполеону и его маршалам и такие планы русским военачальникам. Все факты совершенно противоречат таким предположениям. Не только во все время войны со стороны русских не было желания заманить французов в глубь России, но все было делаемо для того, чтобы остановить их с первого вступления их в Россию, и не только Наполеон не боялся растяжения своей линии, но он радовался, как торжеству, каждому своему шагу вперед и очень лениво, не так, как в прежние свои кампании, искал сражения.
При самом начале кампании армии наши разрезаны, и единственная цель, к которой мы стремимся, состоит в том, чтобы соединить их, хотя для того, чтобы отступать и завлекать неприятеля в глубь страны, в соединении армий не представляется выгод. Император находится при армии для воодушевления ее в отстаивании каждого шага русской земли, а не для отступления. Устроивается громадный Дрисский лагерь по плану Пфуля и не предполагается отступать далее. Государь делает упреки главнокомандующим за каждый шаг отступления. Не только сожжение Москвы, но допущение неприятеля до Смоленска не может даже представиться воображению императора, и когда армии соединяются, то государь негодует за то, что Смоленск взят и сожжен и не дано пред стенами его генерального сражения.
Так думает государь, но русские военачальники и все русские люди еще более негодуют при мысли о том, что наши отступают в глубь страны.
Наполеон, разрезав армии, движется в глубь страны и упускает несколько случаев сражения. В августе месяце он в Смоленске и думает только о том, как бы ему идти дальше, хотя, как мы теперь видим, это движение вперед для него очевидно пагубно.
Факты говорят очевидно, что ни Наполеон не предвидел опасности в движении на Москву, ни Александр и русские военачальники не думали тогда о заманивании Наполеона, а думали о противном. Завлечение Наполеона в глубь страны произошло не по чьему нибудь плану (никто и не верил в возможность этого), а произошло от сложнейшей игры интриг, целей, желаний людей – участников войны, не угадывавших того, что должно быть, и того, что было единственным спасением России. Все происходит нечаянно. Армии разрезаны при начале кампании. Мы стараемся соединить их с очевидной целью дать сражение и удержать наступление неприятеля, но и этом стремлении к соединению, избегая сражений с сильнейшим неприятелем и невольно отходя под острым углом, мы заводим французов до Смоленска. Но мало того сказать, что мы отходим под острым углом потому, что французы двигаются между обеими армиями, – угол этот делается еще острее, и мы еще дальше уходим потому, что Барклай де Толли, непопулярный немец, ненавистен Багратиону (имеющему стать под его начальство), и Багратион, командуя 2 й армией, старается как можно дольше не присоединяться к Барклаю, чтобы не стать под его команду. Багратион долго не присоединяется (хотя в этом главная цель всех начальствующих лиц) потому, что ему кажется, что он на этом марше ставит в опасность свою армию и что выгоднее всего для него отступить левее и южнее, беспокоя с фланга и тыла неприятеля и комплектуя свою армию в Украине. А кажется, и придумано это им потому, что ему не хочется подчиняться ненавистному и младшему чином немцу Барклаю.
Император находится при армии, чтобы воодушевлять ее, а присутствие его и незнание на что решиться, и огромное количество советников и планов уничтожают энергию действий 1 й армии, и армия отступает.
В Дрисском лагере предположено остановиться; но неожиданно Паулучи, метящий в главнокомандующие, своей энергией действует на Александра, и весь план Пфуля бросается, и все дело поручается Барклаю, Но так как Барклай не внушает доверия, власть его ограничивают.
Армии раздроблены, нет единства начальства, Барклай не популярен; но из этой путаницы, раздробления и непопулярности немца главнокомандующего, с одной стороны, вытекает нерешительность и избежание сражения (от которого нельзя бы было удержаться, ежели бы армии были вместе и не Барклай был бы начальником), с другой стороны, – все большее и большее негодование против немцев и возбуждение патриотического духа.
Наконец государь уезжает из армии, и как единственный и удобнейший предлог для его отъезда избирается мысль, что ему надо воодушевить народ в столицах для возбуждения народной войны. И эта поездка государя и Москву утрояет силы русского войска.
Государь отъезжает из армии для того, чтобы не стеснять единство власти главнокомандующего, и надеется, что будут приняты более решительные меры; но положение начальства армий еще более путается и ослабевает. Бенигсен, великий князь и рой генерал адъютантов остаются при армии с тем, чтобы следить за действиями главнокомандующего и возбуждать его к энергии, и Барклай, еще менее чувствуя себя свободным под глазами всех этих глаз государевых, делается еще осторожнее для решительных действий и избегает сражений.
Барклай стоит за осторожность. Цесаревич намекает на измену и требует генерального сражения. Любомирский, Браницкий, Влоцкий и тому подобные так раздувают весь этот шум, что Барклай, под предлогом доставления бумаг государю, отсылает поляков генерал адъютантов в Петербург и входит в открытую борьбу с Бенигсеном и великим князем.
В Смоленске, наконец, как ни не желал того Багратион, соединяются армии.
Багратион в карете подъезжает к дому, занимаемому Барклаем. Барклай надевает шарф, выходит навстречу v рапортует старшему чином Багратиону. Багратион, в борьбе великодушия, несмотря на старшинство чина, подчиняется Барклаю; но, подчинившись, еще меньше соглашается с ним. Багратион лично, по приказанию государя, доносит ему. Он пишет Аракчееву: «Воля государя моего, я никак вместе с министром (Барклаем) не могу. Ради бога, пошлите меня куда нибудь хотя полком командовать, а здесь быть не могу; и вся главная квартира немцами наполнена, так что русскому жить невозможно, и толку никакого нет. Я думал, истинно служу государю и отечеству, а на поверку выходит, что я служу Барклаю. Признаюсь, не хочу». Рой Браницких, Винцингероде и тому подобных еще больше отравляет сношения главнокомандующих, и выходит еще меньше единства. Сбираются атаковать французов перед Смоленском. Посылается генерал для осмотра позиции. Генерал этот, ненавидя Барклая, едет к приятелю, корпусному командиру, и, просидев у него день, возвращается к Барклаю и осуждает по всем пунктам будущее поле сражения, которого он не видал.
Пока происходят споры и интриги о будущем поле сражения, пока мы отыскиваем французов, ошибившись в их месте нахождения, французы натыкаются на дивизию Неверовского и подходят к самым стенам Смоленска.
Надо принять неожиданное сражение в Смоленске, чтобы спасти свои сообщения. Сражение дается. Убиваются тысячи с той и с другой стороны.
Смоленск оставляется вопреки воле государя и всего народа. Но Смоленск сожжен самими жителями, обманутыми своим губернатором, и разоренные жители, показывая пример другим русским, едут в Москву, думая только о своих потерях и разжигая ненависть к врагу. Наполеон идет дальше, мы отступаем, и достигается то самое, что должно было победить Наполеона.


На другой день после отъезда сына князь Николай Андреич позвал к себе княжну Марью.
– Ну что, довольна теперь? – сказал он ей, – поссорила с сыном! Довольна? Тебе только и нужно было! Довольна?.. Мне это больно, больно. Я стар и слаб, и тебе этого хотелось. Ну радуйся, радуйся… – И после этого княжна Марья в продолжение недели не видала своего отца. Он был болен и не выходил из кабинета.
К удивлению своему, княжна Марья заметила, что за это время болезни старый князь так же не допускал к себе и m lle Bourienne. Один Тихон ходил за ним.
Через неделю князь вышел и начал опять прежнюю жизнь, с особенной деятельностью занимаясь постройками и садами и прекратив все прежние отношения с m lle Bourienne. Вид его и холодный тон с княжной Марьей как будто говорил ей: «Вот видишь, ты выдумала на меня налгала князю Андрею про отношения мои с этой француженкой и поссорила меня с ним; а ты видишь, что мне не нужны ни ты, ни француженка».
Одну половину дня княжна Марья проводила у Николушки, следя за его уроками, сама давала ему уроки русского языка и музыки, и разговаривая с Десалем; другую часть дня она проводила в своей половине с книгами, старухой няней и с божьими людьми, которые иногда с заднего крыльца приходили к ней.
О войне княжна Марья думала так, как думают о войне женщины. Она боялась за брата, который был там, ужасалась, не понимая ее, перед людской жестокостью, заставлявшей их убивать друг друга; но не понимала значения этой войны, казавшейся ей такою же, как и все прежние войны. Она не понимала значения этой войны, несмотря на то, что Десаль, ее постоянный собеседник, страстно интересовавшийся ходом войны, старался ей растолковать свои соображения, и несмотря на то, что приходившие к ней божьи люди все по своему с ужасом говорили о народных слухах про нашествие антихриста, и несмотря на то, что Жюли, теперь княгиня Друбецкая, опять вступившая с ней в переписку, писала ей из Москвы патриотические письма.
«Я вам пишу по русски, мой добрый друг, – писала Жюли, – потому что я имею ненависть ко всем французам, равно и к языку их, который я не могу слышать говорить… Мы в Москве все восторжены через энтузиазм к нашему обожаемому императору.
Бедный муж мой переносит труды и голод в жидовских корчмах; но новости, которые я имею, еще более воодушевляют меня.
Вы слышали, верно, о героическом подвиге Раевского, обнявшего двух сыновей и сказавшего: «Погибну с ними, но не поколеблемся!И действительно, хотя неприятель был вдвое сильнее нас, мы не колебнулись. Мы проводим время, как можем; но на войне, как на войне. Княжна Алина и Sophie сидят со мною целые дни, и мы, несчастные вдовы живых мужей, за корпией делаем прекрасные разговоры; только вас, мой друг, недостает… и т. д.
Преимущественно не понимала княжна Марья всего значения этой войны потому, что старый князь никогда не говорил про нее, не признавал ее и смеялся за обедом над Десалем, говорившим об этой войне. Тон князя был так спокоен и уверен, что княжна Марья, не рассуждая, верила ему.
Весь июль месяц старый князь был чрезвычайно деятелен и даже оживлен. Он заложил еще новый сад и новый корпус, строение для дворовых. Одно, что беспокоило княжну Марью, было то, что он мало спал и, изменив свою привычку спать в кабинете, каждый день менял место своих ночлегов. То он приказывал разбить свою походную кровать в галерее, то он оставался на диване или в вольтеровском кресле в гостиной и дремал не раздеваясь, между тем как не m lle Bourienne, a мальчик Петруша читал ему; то он ночевал в столовой.
Первого августа было получено второе письмо от кня зя Андрея. В первом письме, полученном вскоре после его отъезда, князь Андрей просил с покорностью прощения у своего отца за то, что он позволил себе сказать ему, и просил его возвратить ему свою милость. На это письмо старый князь отвечал ласковым письмом и после этого письма отдалил от себя француженку. Второе письмо князя Андрея, писанное из под Витебска, после того как французы заняли его, состояло из краткого описания всей кампании с планом, нарисованным в письме, и из соображений о дальнейшем ходе кампании. В письме этом князь Андрей представлял отцу неудобства его положения вблизи от театра войны, на самой линии движения войск, и советовал ехать в Москву.
За обедом в этот день на слова Десаля, говорившего о том, что, как слышно, французы уже вступили в Витебск, старый князь вспомнил о письме князя Андрея.
– Получил от князя Андрея нынче, – сказал он княжне Марье, – не читала?
– Нет, mon pere, [батюшка] – испуганно отвечала княжна. Она не могла читать письма, про получение которого она даже и не слышала.
– Он пишет про войну про эту, – сказал князь с той сделавшейся ему привычной, презрительной улыбкой, с которой он говорил всегда про настоящую войну.
– Должно быть, очень интересно, – сказал Десаль. – Князь в состоянии знать…
– Ах, очень интересно! – сказала m llе Bourienne.
– Подите принесите мне, – обратился старый князь к m llе Bourienne. – Вы знаете, на маленьком столе под пресс папье.
M lle Bourienne радостно вскочила.
– Ах нет, – нахмурившись, крикнул он. – Поди ты, Михаил Иваныч.
Михаил Иваныч встал и пошел в кабинет. Но только что он вышел, старый князь, беспокойно оглядывавшийся, бросил салфетку и пошел сам.
– Ничего то не умеют, все перепутают.
Пока он ходил, княжна Марья, Десаль, m lle Bourienne и даже Николушка молча переглядывались. Старый князь вернулся поспешным шагом, сопутствуемый Михаилом Иванычем, с письмом и планом, которые он, не давая никому читать во время обеда, положил подле себя.
Перейдя в гостиную, он передал письмо княжне Марье и, разложив пред собой план новой постройки, на который он устремил глаза, приказал ей читать вслух. Прочтя письмо, княжна Марья вопросительно взглянула на отца.
Он смотрел на план, очевидно, погруженный в свои мысли.
– Что вы об этом думаете, князь? – позволил себе Десаль обратиться с вопросом.
– Я! я!.. – как бы неприятно пробуждаясь, сказал князь, не спуская глаз с плана постройки.
– Весьма может быть, что театр войны так приблизится к нам…
– Ха ха ха! Театр войны! – сказал князь. – Я говорил и говорю, что театр войны есть Польша, и дальше Немана никогда не проникнет неприятель.
Десаль с удивлением посмотрел на князя, говорившего о Немане, когда неприятель был уже у Днепра; но княжна Марья, забывшая географическое положение Немана, думала, что то, что ее отец говорит, правда.
– При ростепели снегов потонут в болотах Польши. Они только могут не видеть, – проговорил князь, видимо, думая о кампании 1807 го года, бывшей, как казалось, так недавно. – Бенигсен должен был раньше вступить в Пруссию, дело приняло бы другой оборот…
– Но, князь, – робко сказал Десаль, – в письме говорится о Витебске…
– А, в письме, да… – недовольно проговорил князь, – да… да… – Лицо его приняло вдруг мрачное выражение. Он помолчал. – Да, он пишет, французы разбиты, при какой это реке?
Десаль опустил глаза.
– Князь ничего про это не пишет, – тихо сказал он.
– А разве не пишет? Ну, я сам не выдумал же. – Все долго молчали.
– Да… да… Ну, Михайла Иваныч, – вдруг сказал он, приподняв голову и указывая на план постройки, – расскажи, как ты это хочешь переделать…
Михаил Иваныч подошел к плану, и князь, поговорив с ним о плане новой постройки, сердито взглянув на княжну Марью и Десаля, ушел к себе.
Княжна Марья видела смущенный и удивленный взгляд Десаля, устремленный на ее отца, заметила его молчание и была поражена тем, что отец забыл письмо сына на столе в гостиной; но она боялась не только говорить и расспрашивать Десаля о причине его смущения и молчания, но боялась и думать об этом.
Ввечеру Михаил Иваныч, присланный от князя, пришел к княжне Марье за письмом князя Андрея, которое забыто было в гостиной. Княжна Марья подала письмо. Хотя ей это и неприятно было, она позволила себе спросить у Михаила Иваныча, что делает ее отец.
– Всё хлопочут, – с почтительно насмешливой улыбкой, которая заставила побледнеть княжну Марью, сказал Михаил Иваныч. – Очень беспокоятся насчет нового корпуса. Читали немножко, а теперь, – понизив голос, сказал Михаил Иваныч, – у бюра, должно, завещанием занялись. (В последнее время одно из любимых занятий князя было занятие над бумагами, которые должны были остаться после его смерти и которые он называл завещанием.)
– А Алпатыча посылают в Смоленск? – спросила княжна Марья.
– Как же с, уж он давно ждет.


Когда Михаил Иваныч вернулся с письмом в кабинет, князь в очках, с абажуром на глазах и на свече, сидел у открытого бюро, с бумагами в далеко отставленной руке, и в несколько торжественной позе читал свои бумаги (ремарки, как он называл), которые должны были быть доставлены государю после его смерти.
Когда Михаил Иваныч вошел, у него в глазах стояли слезы воспоминания о том времени, когда он писал то, что читал теперь. Он взял из рук Михаила Иваныча письмо, положил в карман, уложил бумаги и позвал уже давно дожидавшегося Алпатыча.
На листочке бумаги у него было записано то, что нужно было в Смоленске, и он, ходя по комнате мимо дожидавшегося у двери Алпатыча, стал отдавать приказания.
– Первое, бумаги почтовой, слышишь, восемь дестей, вот по образцу; золотообрезной… образчик, чтобы непременно по нем была; лаку, сургучу – по записке Михаила Иваныча.
Он походил по комнате и заглянул в памятную записку.
– Потом губернатору лично письмо отдать о записи.
Потом были нужны задвижки к дверям новой постройки, непременно такого фасона, которые выдумал сам князь. Потом ящик переплетный надо было заказать для укладки завещания.
Отдача приказаний Алпатычу продолжалась более двух часов. Князь все не отпускал его. Он сел, задумался и, закрыв глаза, задремал. Алпатыч пошевелился.
– Ну, ступай, ступай; ежели что нужно, я пришлю.
Алпатыч вышел. Князь подошел опять к бюро, заглянув в него, потрогал рукою свои бумаги, опять запер и сел к столу писать письмо губернатору.
Уже было поздно, когда он встал, запечатав письмо. Ему хотелось спать, но он знал, что не заснет и что самые дурные мысли приходят ему в постели. Он кликнул Тихона и пошел с ним по комнатам, чтобы сказать ему, где стлать постель на нынешнюю ночь. Он ходил, примеривая каждый уголок.
Везде ему казалось нехорошо, но хуже всего был привычный диван в кабинете. Диван этот был страшен ему, вероятно по тяжелым мыслям, которые он передумал, лежа на нем. Нигде не было хорошо, но все таки лучше всех был уголок в диванной за фортепиано: он никогда еще не спал тут.
Тихон принес с официантом постель и стал уставлять.
– Не так, не так! – закричал князь и сам подвинул на четверть подальше от угла, и потом опять поближе.
«Ну, наконец все переделал, теперь отдохну», – подумал князь и предоставил Тихону раздевать себя.
Досадливо морщась от усилий, которые нужно было делать, чтобы снять кафтан и панталоны, князь разделся, тяжело опустился на кровать и как будто задумался, презрительно глядя на свои желтые, иссохшие ноги. Он не задумался, а он медлил перед предстоявшим ему трудом поднять эти ноги и передвинуться на кровати. «Ох, как тяжело! Ох, хоть бы поскорее, поскорее кончились эти труды, и вы бы отпустили меня! – думал он. Он сделал, поджав губы, в двадцатый раз это усилие и лег. Но едва он лег, как вдруг вся постель равномерно заходила под ним вперед и назад, как будто тяжело дыша и толкаясь. Это бывало с ним почти каждую ночь. Он открыл закрывшиеся было глаза.